【問題】
【難易度】★★★★☆(やや難しい)
図に示す閉ループ制御系の特性根を求めるための特性方程式は,\( \ 1+G(s)H(s)=0 \ \)である。
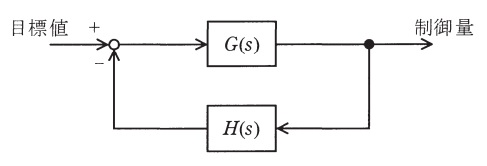
いま,一巡伝達関数\( \ G(s)H(s) \ \)が
\[
\begin{eqnarray}
G(s)H(s)&=&\frac {K}{s (s+1) (s+2)} \\[ 5pt ]
\end{eqnarray}
\]
で与えられている。このパラメータ\( \ K \ \)を\( \ K=0 \ \)から\( \ K=+\infty \ \)まで変化させるときの閉ループ制御系の特性根の軌跡(根軌跡)を,右ページに示す(a)~(f)を参考にして次の(1)~(7)の手順で描け。
(1) 右ページの(c)から求められる実軸上の根軌跡の区間を示せ。
(2) 漸近線の実軸との交点\( \ \sigma _{\mathrm {c}} \ \)及び漸近線の角度\(\theta \)を求めよ。
(3) 答案用紙に印刷されている複素平面上に,実軸上の根軌跡を太い実線,漸近線を破線で描け。
(4) 根軌跡が分岐する点を求めよ。また,そのときの\( \ K \ \)の値を求めよ。
(5) ラウス・フルビッツの安定判別法を用いて安定限界となる\( \ K \ \)の値を求めよ。
(6) 根軌跡と虚軸との交点を求めよ。
(7) 以上の結果から,根軌跡の概形を答案用紙に印刷されている複素平面上に描け。
(以下右ページ)
\([\)根軌跡法\(] \)
一巡伝達関数が次式で与えられている。
\[
\begin{eqnarray}
G(s)H(s)&=&\frac {K( s-z_{1}) ( s-z_{2}) \cdots ( s-z_{m} ) }{ ( s-p_{1} ) ( s-p_{2} ) \cdots (s-p_{n} ) },n > m \\[ 5pt ]
\end{eqnarray}
\]
ただし,極\( \ p_{i},i=1,2,\cdots ,n \ \)と零点\( \ z_{i},i=1,2,\cdots ,m \ \)は,実数又は共役複素数とする。このとき,根軌跡は以下にまとめる根軌跡法を用いてその概形を描くことができる。
(a) 実軸対称である。
(b) 一巡伝達関数の極から出発して,\( \ m \ \)個は零点に収束し,残りは無限遠に発散する。
(c) 実軸上の根軌跡の区間は,極と零点で区切られる区間のうち,右から奇数番目である。
(d) 漸近線の実軸との交点\( \ \sigma _{\mathrm {c}} \ \)及び漸近線の角度\( \ \theta \ \)は以下のように計算される。
\[
\begin{eqnarray}
&&\sigma _{\mathrm {c}} =\frac {1}{n-m}\left( \displaystyle \sum_{ i = 1 }^{ n } p_{i} -\displaystyle \sum_{ i = 1 }^{ m } z_{i}\right) \\[ 5pt ]
&&\theta =\frac {N\pi }{n-m},N=±1,±3,±5,\cdots \\[ 5pt ]
\end{eqnarray}
\]
(e) 分岐点では次式を満たす。
\[
\begin{eqnarray}
\frac {1}{s-p_{1}}+\frac {1}{s-p_{2}}+\cdots +\frac {1}{s-p_{n}}-\frac {1}{s-z_{1}}-\frac {1}{s-z_{2}}-\cdots -\frac {1}{s-z_{m}}=0 \\[ 5pt ]
\end{eqnarray}
\]
(f) 虚軸との交点は,ラウス・フルビッツの安定判別法から求められる。
【ワンポイント解説】
過去に出題されたことがない問題が出題され,受験生も大変苦労した問題であると思います。さすがに,本問を初見で解くことは難しいと思います。以下のラウス・フルビッツの安定判別法は電験一種では必須の内容となりますので,よく理解しておきましょう。
1.ラウスの安定判別法
特性方程式\( \ a_{0}s^{n}+a_{1}s^{n-1}+a_{2}s^{n-2}+\cdots +a_{n-1}s+a_{n}=0 \ \)が与えられているとき,ラウスの数表は下表にように描くことができ,\( \ 1 \ \)列の値がすべて同符号であるとき,制御系は安定であると判別できます。
\[
\begin{array}{c|ccc}
& \color {red} {1 \ 列} & 2 \ 列 & 3 \ 列 \\
\hline
1 \ 行 & \color {red} {a_{0}} & a_{2} & a_{4} & \cdots \\
2 \ 行 & \color {red} {a_{1}} & a_{3} & a_{5} & \cdots \\
3 \ 行 & \color {red} {b_{1}=\frac {a_{1}a_{2}-a_{0}a_{3}}{a_{1}}} & b_{2}=\frac {a_{1}a_{4}-a_{0}a_{5}}{a_{1}} & \cdots \\
4 \ 行 & \color {red} {c_{1}=\frac {b_{1}a_{3}-a_{1}b_{2}}{b_{1}}} & c_{2}=\frac {b_{1}a_{5}-a_{1}b_{3}}{b_{1}} & \cdots \\
\vdots & \color {red} {\vdots } & \vdots &
\end{array}
\]
【解答】
(1)実軸上の根軌跡の区間
一巡伝達関数を根軌跡法に与えられた式と比較すると,\( \ n=3 \ \),\( \ m=0 \ \)となる。
また,極\( \ p_{1}=0 \ \),\( \ p_{2}=-1 \ \),\( \ p_{3}=-2 \ \)であり,零点はなしとなる。
よって,極\( \ p_{1}=0 \ \),\( \ p_{2}=-1 \ \),\( \ p_{3}=-2 \ \)で区切られる区間のうち,右から奇数番目の区間は,\( \ -1~0 \ \),\( \ -\infty ~-2 \ \)の区間となる。
(2)漸近線の実軸との交点\(\sigma _{\mathrm {c}}\)及び漸近線の角度\(\theta \)
(d)より実軸との交点\( \ \sigma _{\mathrm {c}} \ \)及び漸近線の角度\( \ \theta \ \)は,
\[
\begin{eqnarray}
\sigma _{\mathrm {c}} &=&\frac {1}{3-0}\left( \displaystyle \sum_{ i = 1 }^{ 3 } p_{i} -\displaystyle \sum_{ i = 1 }^{ 0 } z_{i}\right) \\[ 5pt ]
&=&\frac {1}{3}\left( p_{1} +p_{2}+p_{3}\right) \\[ 5pt ]
&=&\frac {1}{3}\left( 0 -1-2\right) \\[ 5pt ]
&=&-1
\end{eqnarray}
\]
\[
\begin{eqnarray}
\theta &=&\frac {N\pi }{3-0},N=±1,±3,±5,\cdots \\[ 5pt ]
&=&±\frac {\pi }{3},±\pi ,±\frac {5\pi }{3},\cdots
\end{eqnarray}
\]
と求められる。
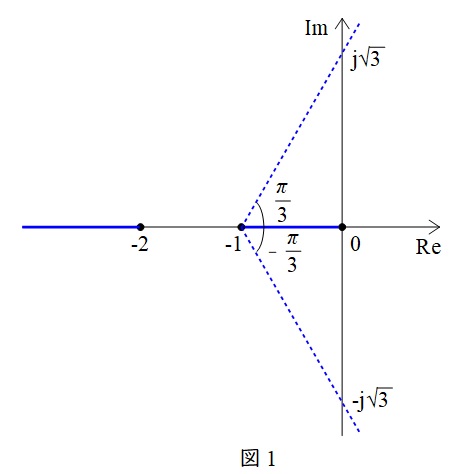
(3)実軸上の根軌跡を太い実線,漸近線を破線で描く
(1)と(2)の計算結果を集約すると,図1の通りとなる。
(4)根軌跡が分岐する点及びそのときの\( \ K \ \)の値
(e)の式に\( \ p_{1}=0 \ \),\( \ p_{2}=-1 \ \),\( \ p_{3}=-2 \ \)を代入すると,
\[
\begin{eqnarray}
&&\frac {1}{s}+\frac {1}{s+1}+\frac {1}{s+2}=0 \\[ 5pt ]
\end{eqnarray}
\]
となるので,式を変形し,\( \ s \ \)を求めると,
\[
\begin{eqnarray}
\frac { (s+1) (s+2) +s ( s+2) + s ( s+1 ) }{s (s+1) (s+2) } &=& 0 \\[ 5pt ]
(s+1) (s+2) +s ( s+2) + s ( s+1 ) &=& 0 \\[ 5pt ]
3s^{2}+6s+ 2 &=& 0 \\[ 5pt ]
s &=& \frac {-3±\sqrt{3}}{3} \\[ 5pt ]
&≒&-0.42265,-1.5774 \\[ 5pt ]
\end{eqnarray}
\]
となる。図1より,分岐点は\( \ -1 \ \)から\( \ 0 \ \)の間にあるので,分岐点は\( \ -0.423 \ \)となる。
また,特性方程式に\( \ s \ \)の値を代入し,\( \ K \ \)の値を求めると,
\[
\begin{eqnarray}
1+G (s ) H ( s )&=&0 \\[ 5pt ]
1+\frac {K}{s (s+1) (s+2)}&=&0 \\[ 5pt ]
K&=&-s (s+1) (s+2) \\[ 5pt ]
K&=&- ( -0.42265 )( -0.42265+1 ) ( -0.42265+2 ) \\[ 5pt ]
K&=&0.38490 → 0.385 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)安定限界となる\( \ K \ \)
特性方程式は\( \ s^{3}+3s^{2}+2s+K=0 \ \)と整理できるので,ワンポイント解説「1.ラウスの安定判別法」に沿って安定判別すると,
係数がすべて正である → \( \ K > 0 \ \)
ラウス表を作成すると下表のようになる。
\[
\begin{array}{c|cc}
& 1 & 2 \\
\hline
1 & 1 & 2 \\
2 & 3 & K \\
3 & \cfrac {6-K}{3} & 0 \\
4 & K & 0 \\
\end{array}
\]
よって,3行1列目の式より\(K < 6 \)となる。したがって安定限界となるのは,\(K=0,6\)の時である。
(6)根軌跡と虚軸との交点
\( \ K=0 \ \)は\( \ s=0 \ \)が安定限界であることを示しているので,虚軸との交点となるのは\( \ K=6 \ \)の時である。特性方程式に\( \ K=6 \ \)を代入して\( \ s \ \)の値を求めると,
\[
\begin{eqnarray}
s^{3}+3s^{2}+2s+6&=&0 \\[ 5pt ]
s^{2} ( s+3 ) +2 (s+3 ) &=&0 \\[ 5pt ]
( s+3 ) (s^{2} +2 ) &=&0 \\[ 5pt ]
s&=&-3,±\mathrm {j}\sqrt {2}
\end{eqnarray}
\]
となり,虚軸との交点として適しているのは\( \ s=±\mathrm {j}\sqrt {2} \ \)となる。
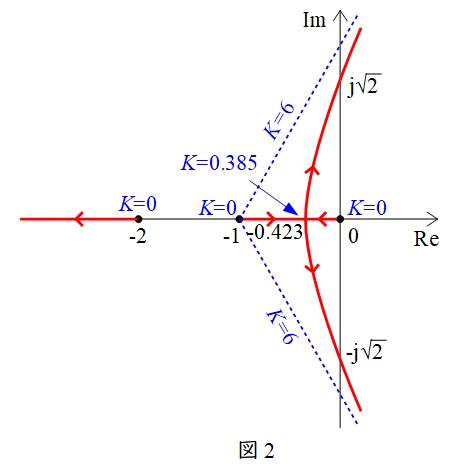
(7)根軌跡の概形
(5),(6)より,根軌跡の概形は図2のようになる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん