《機械・制御》〈自動制御〉[R01:問4]フィードバック制御に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

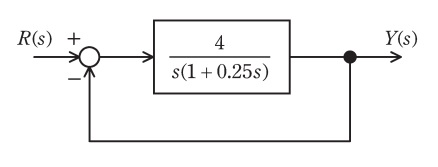
図のようなフィードバック制御系がある。ここで\( \ R(s) \ \)と\( \ Y(s) \ \)は，それぞれ目標値\( \ r(t) \ \)と制御量\( \ y(t) \ \)のラプラス変換である。次の問に答えよ。

(1)　\( \ 2 \ \)次遅れ系の標準形\( \ \displaystyle G(s)=\frac {\omega _{\mathrm {n}}^{2}}{s^{2}+2\zeta \omega _{\mathrm {n}}s+\omega _{\mathrm {n}}^{2}} \ \)を考える。ここで，\( \ \omega _{\mathrm {n}} \ \mathrm {[rad/s]} \ \)は固有角周波数，\( \ \zeta \ \)は減衰係数であり，\( \ \omega _{\mathrm {n}} ＞0 \ \)，\( \ \displaystyle 0＜\zeta ＜\frac {\sqrt {2}}{2} \ \)とする。周波数応答の振幅\( \ \left| G(\mathrm {j}\omega ) \right| \ \)が\( \ \displaystyle \left| G(\mathrm {j}\omega ) \right| =\frac {1}{\sqrt {\left( 1-x\right) ^{2}+4\zeta ^{2}x}} \ \)で与えられることを示せ。ただし，\( \ \displaystyle x≜\left( \frac {\omega }{\omega _{\mathrm {n}}}\right) ^{2} \ \)とする。

(2)　関数\( \ f(x)=\left( 1-x\right) ^{2}+4\zeta ^{2}x \ \)を最小にする\( \ x \ \)を\( \ x_{\mathrm {p}} \ \)とするとき，\( \ x_{\mathrm {p}} \ \)を\( \ \zeta \ \)で表せ。また，周波数応答の振幅\( \ \left| G(\mathrm {j}\omega ) \right| \ \)の最大値\( \ M_{\mathrm {p}} \ \)を\( \ \zeta \ \)で表せ。

(3)　図のフィードバック制御系の閉ループ伝達関数\( \ G_{\mathrm {c}}(s) \ \)を求めよ。また，\( \ \omega _{\mathrm {n}} \ \)及び\( \ \zeta \ \)の値を求めよ。

(4)　小問(3)で求めた閉ループ伝達関数\( \ G_{\mathrm {c}}(s) \ \)の周波数応答の振幅を最大にする角周波数\( \ \omega _{\mathrm {p}} \ \mathrm {[rad/s]} \ \)及び最大振幅\( \ M_{\mathrm {p}} \ \)の値を求めよ。

【ワンポイント解説】

１種には珍しい古典制御からオーソドックスな出題となっています。比較的時間も余裕のある問題なので，計算ミスに注意して確実に点を取りたい問題と言えるでしょう。

【解答】

(1)周波数応答の振幅\( \ \left| G(\mathrm {j}\omega ) \right| \ \)が\( \ \displaystyle \left| G(\mathrm {j}\omega ) \right| =\frac {1}{\sqrt {\left( 1-x\right) ^{2}+4\zeta ^{2}x}} \ \)で与えられることを示す
\( \ 2 \ \)次遅れ系の標準形\( \ \displaystyle G(s)=\frac {\omega _{\mathrm {n}}^{2}}{s^{2}+2\zeta \omega _{\mathrm {n}}s+\omega _{\mathrm {n}}^{2}} \ \)の周波数応答を求めるため，\( \ s=\mathrm {j}\omega \ \)を代入すると，
\[
\begin{eqnarray}
G(\mathrm {j}\omega )&=&\frac {\omega _{\mathrm {n}}^{2}}{-\omega ^{2}+\mathrm {j}2\zeta \omega _{\mathrm {n}}\omega +\omega _{\mathrm {n}}^{2}} \\[ 5pt ] &=&\frac {1}{\displaystyle 1-\frac {\omega ^{2}}{\omega _{\mathrm {n}} ^{2}}+\mathrm {j}2\zeta \frac {\omega }{\omega _{\mathrm {n}}}} \\[ 5pt ] \end{eqnarray}
\] であるから，その絶対値は，
\[
\begin{eqnarray}
\left| G(\mathrm {j}\omega ) \right| &=&\frac {1}{\displaystyle \sqrt { \left( 1-\frac {\omega ^{2}}{\omega _{\mathrm {n}} ^{2}}\right) ^{2}+4\zeta ^{2}\left( \frac {\omega }{\omega _{\mathrm {n}}}\right) ^{2}}} \\[ 5pt ] &=&\frac {1}{\displaystyle \sqrt { \left( 1-x\right) ^{2}+4\zeta ^{2}x}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)\( \ x_{\mathrm {p}} \ \)及び\( \ M_{\mathrm {p}} \ \)を\( \ \zeta \ \)で表す
\( \ f(x)=\left( 1-x\right) ^{2}+4\zeta ^{2}x \ \)を展開すると，
\[
\begin{eqnarray}
f(x) &=&1-2x+x^{2}+4\zeta ^{2}x \\[ 5pt ] &=&x^{2}+\left( 4\zeta ^{2}-2\right) x+1 \\[ 5pt ] \end{eqnarray}
\] となるので，両辺微分すると，
\[
\begin{eqnarray}
\frac {\mathrm {d}f(x)}{\mathrm {d}x} &=&2x+4\zeta ^{2}-2 \\[ 5pt ] \end{eqnarray}
\] となり，最小値をとるのは\( \ \displaystyle \frac {\mathrm {d}f(x)}{\mathrm {d}x}=0 \ \)の時であるから，
\[
\begin{eqnarray}
2x_{\mathrm {p}}+4\zeta ^{2}-2 &=&0 \\[ 5pt ] x_{\mathrm {p}} &=&1-2\zeta ^{2} \\[ 5pt ] \end{eqnarray}
\] と求められる。よって，周波数応答の振幅最大値\( \ M_{\mathrm {p}} \ \)は，
\[
\begin{eqnarray}
M_{\mathrm {p}} &=&\frac {1}{\displaystyle \sqrt { \left( 1-x_{\mathrm {p}} \right) ^{2}+4\zeta ^{2}x_{\mathrm {p}} }} \\[ 5pt ] &=&\frac {1}{\displaystyle \sqrt { \left\{ 1-\left( 1-2\zeta ^{2}\right) \right\} ^{2}+4\zeta ^{2}\left( 1-2\zeta ^{2}\right) }} \\[ 5pt ] &=&\frac {1}{\displaystyle \sqrt { 4\zeta ^{4}+4\zeta ^{2}-8\zeta ^{4} }} \\[ 5pt ] &=&\frac {1}{\displaystyle \sqrt { 4\zeta ^{2}-4\zeta ^{4} }} \\[ 5pt ] &=&\frac {1}{\displaystyle 2\zeta \sqrt { 1-\zeta ^{2} }} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)閉ループ伝達関数\( \ G_{\mathrm {c}}(s) \ \)，\( \ \omega _{\mathrm {n}} \ \)及び\( \ \zeta \ \)の値
問題図より，
\[
\begin{eqnarray}
\left\{ R(s)-Y(s)\right\} \frac {4}{s\left( 1+0.25s\right) }&=&Y(s) \\[ 5pt ] 4R(s)-4Y(s)&=&s\left( 1+0.25s\right) Y(s) \\[ 5pt ] 4R(s)&=&\left( 0.25s^{2}+s+4\right) Y(s) \\[ 5pt ] \frac {Y(s)}{R(s)}&=&\frac {4}{0.25s^{2}+s+4} \\[ 5pt ] G_{\mathrm {c}}(s) &=&\frac {16}{s^{2}+4s+16} \\[ 5pt ] \end{eqnarray}
\] と求められる。これを\( \ 2 \ \)次遅れ系の標準形\( \ \displaystyle G(s)=\frac {\omega _{\mathrm {n}}^{2}}{s^{2}+2\zeta \omega _{\mathrm {n}}s+\omega _{\mathrm {n}}^{2}} \ \)と係数比較すると，
\[
\begin{eqnarray}
\omega _{\mathrm {n}}^{2} &=&16 \\[ 5pt ] 2\zeta \omega _{\mathrm {n}} &=&4 \\[ 5pt ] \end{eqnarray}
\] となるので，これらの方程式を解くと，
\[
\begin{eqnarray}
\omega _{\mathrm {n}} &=&4 \ \mathrm {[rad ／s]} \\[ 5pt ] \zeta &=&0.5 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)周波数応答の振幅を最大にする角周波数\( \ \omega _{\mathrm {p}} \ \mathrm {[rad/s]} \ \)及び最大振幅\( \ M_{\mathrm {p}} \ \)の値
(2)より，\( \ G_{\mathrm {c}}(s) \ \)の周波数応答の振幅を最大にする角周波数\( \ \omega _{\mathrm {p}} \ \mathrm {[rad/s]} \ \)を満たす条件は，
\[
\begin{eqnarray}
x_{\mathrm {p}}&=&\left( \frac {\omega _{\mathrm {p}}}{\omega _{\mathrm {n}}}\right) ^{2} \\[ 5pt ] \omega _{\mathrm {p}}&=&\omega _{\mathrm {n}}\sqrt {x_{\mathrm {p}}} \\[ 5pt ] &=&\omega _{\mathrm {n}}\sqrt {1-2\zeta ^{2}} \\[ 5pt ] &=&4\times \sqrt {1-2\times 0.5 ^{2}} \\[ 5pt ] &≒&2.8284　→　2.83 \ \mathrm {[rad ／s]} \\[ 5pt ] \end{eqnarray}
\] となり，最大振幅\( \ M_{\mathrm {p}} \ \)の値は，
\[
\begin{eqnarray}
M_{\mathrm {p}} &=&\frac {1}{\displaystyle 2\zeta \sqrt { 1-\zeta ^{2} }} \\[ 5pt ] &=&\frac {1}{\displaystyle 2\times 0.5 \sqrt { 1-0.5 ^{2} }} \\[ 5pt ] &≒&1.1547　→　1.15 \\[ 5pt ] \end{eqnarray}
\] と求められる。