【問題】
【難易度】★★★☆☆(普通)
次の文章は,回路の過渡現象に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまるものを解答群の中から選びなさい。
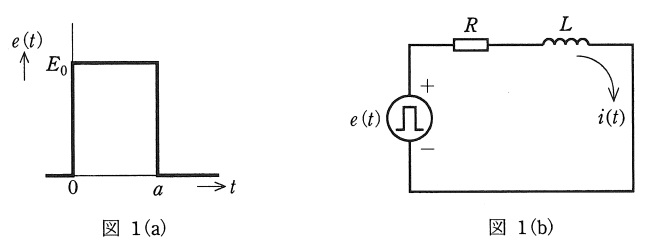
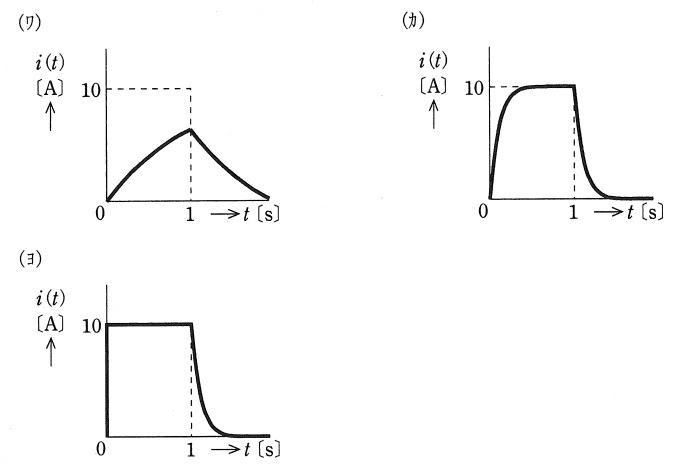
図1(a)の方形パルス電圧\( \ e(t) \ \)(パルス幅\( \ a \ \),大きさ\( \ E_{0} \ \))を図1(b)に示す抵抗\( \ R \ \)とインダクタンス\( \ L \ \)の直列回路に加えたときに流れる電流\( \ i(t) \ \)をラプラス変換によって求め,その波形の概略を描きたい。ただし,回路の初期電流は零とする。
図1(b)よりキルヒホッフの電圧則に従って回路方程式を求め,これをラプラス変換すると\( \ \fbox { (1) } \ \)が得られる。ただし,\(I(s)= \ \mathcal{L} [i(t)],E(s)=\mathcal{L}[e(t)] \ \)(\( \ \mathcal{L}[ ] \ \)は,ラプラス変換を表す。)とする。次に,\( \ e(t) \ \)は単位ステップ関数\( \ u(t) \ \)を用いて表すことができ,これをラプラス変換すると\( \ E(s)=\fbox { (2) } \ \)となる。これを式\( \ \fbox { (1) } \ \)に代入し,\( \ I(s) \ \)を求めると\( \ \fbox { (3) } \ \)となる。以上より,\( \ I(s) \ \)を部分分数に展開し,逆ラプラス変換を行うことにより\( \ i(t) \ \)は\( \ \fbox { (4) } \ \)と求められる。
一例として,\( \ R=1 \ [\Omega],L=100 \ [\mathrm {mH}],E_{0}=10 \ [\mathrm {V}],a=1 \ [\mathrm {s}] \ \)として,この波形の概略を描くと\( \ \fbox { (5) } \ \)となる。
なお,\( \ \mathcal{L}[f(t)]=F(s) \ \)とすると,次の関係が成り立つ。
\[
\begin{eqnarray}
\mathcal{L}[f(t-\alpha)]&=&F(s)\mathrm {e}^{-\alpha s} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
\mathcal{L}[f(t)\mathrm {e}^{\beta t}]&=&F(s-\beta) \\[ 5pt ]
\end{eqnarray}
\]
ただし,\( \ \alpha >0 \ \),\( \ f(t)=0 (t<0) \ \)とする。
〔問4の解答群〕
\[
\begin{eqnarray}
&(イ)& I(s) =\frac {E\left( s\right) }{R}+\frac {E\left( s\right) }{sL} &(ロ)& \frac {E_{0}}{R}\left[ \left( 1-\mathrm {e}^{-\frac {R}{L}t}\right) u\left( t\right) -\left( 1-\mathrm {e}^{-\frac {R}{L}\left( t-a\right) }\right) u\left( t-a\right) \right] \\[ 5pt ]
&(ハ)& E(s)=RI(s)-sLI(s) &(ニ)& \frac {E_{0}}{R}\left[ \left( 1-\mathrm {e}^{-\frac {L}{R}t}\right) u\left( t\right) -\left( 1-\mathrm {e}^{-\frac {L}{R}\left( t-a\right) }\right) u\left( t-a\right) \right] \\[ 5pt ]
&(ホ)& \frac {E_{0}}{s}\left( 1-\mathrm {e}^{-as}\right) &(ヘ)& \frac {E_{0}}{R}\left[ \left( 1-\mathrm {e}^{-RLt}\right) u\left( t\right) -\left( 1-\mathrm {e}^{-RL\left( t-a\right) }\right) u\left( t-a\right) \right] \\[ 5pt ]
&(ト)& \frac {E_{0}\left( 1-\mathrm {e}^{-as}\right) }{\displaystyle Ls\left( s+\frac {R}{L}\right) } &(チ)& E_{0}\left( 1-\mathrm {e}^{-as}\right) \\[ 5pt ]
&(リ)& \frac {E_{0}\left( 1-\mathrm {e}^{-as}\right) }{\displaystyle s\left( s+\frac {R}{L}\right) } &(ヌ)& \frac {E_{0}}{s} \\[ 5pt ]
&(ル)& E(s)=RI(s)+sLI(s) &(ヲ)& \frac {E_{0}\left( 1-\mathrm {e}^{-as}\right) }{\displaystyle L\left( s+\frac {R}{L}\right) } \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
過渡現象をラプラス変換を用いて解く問題です。ラプラス変換をマスターしていればさほど難しい内容ではありません。ラプラス変換は二次試験にも出題される非常に重要な公式です。ぜひラプラス変換とラプラス逆変換は記憶しておいて下さい。
1.基本的なラプラス変換
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると以下のような関係があります。
\[
\begin{array}{|c|c|}
\hline
f(t) & F(s) \\
\hline
u (t) & \displaystyle \frac {1}{s} \\[ 5pt ]
K & \displaystyle \frac {K}{s} \\[ 5pt ]
t & \displaystyle \frac {1}{s^{2}} \\[ 5pt ]
\mathrm {e}^{at} & \displaystyle \frac {1}{s-a} \\[ 5pt ]
\sin \omega t & \displaystyle \frac {\omega }{s^{2}+\omega ^{2}} \\[ 5pt ]
\cos \omega t & \displaystyle \frac {s}{s^{2}+\omega ^{2}} \\[ 5pt ]
\displaystyle f(t-\alpha) & F(s)\mathrm {e}^{-\alpha s} \\[ 5pt ]
\displaystyle \frac {\mathrm {d}f\left( t\right) }{\mathrm {d}t} & sF(s)-f(0) \\[ 5pt ]
\displaystyle \int f\left( t\right) \mathrm {d}t & \displaystyle \frac {F(s)}{s} \\[ 5pt ]
\hline
\end{array}
\]
【解答】
(1)解答:ル
図1(b)の回路方程式は,
\[
\begin{eqnarray}
e(t)&=&Ri(t)+L\frac{\mathrm {d}i}{\mathrm {d}t} \\[ 5pt ]
\end{eqnarray}
\]
となる。両辺をラプラス変換すると,
\[
\begin{eqnarray}
E(s)&=&RI(s)+L \left\{ sI(s)-i(0)\right\} \\[ 5pt ]
\end{eqnarray}
\]
となり,題意より初期電流は零であるから,
\[
\begin{eqnarray}
E(s)&=&RI\left( s\right)+sLI\left( s\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
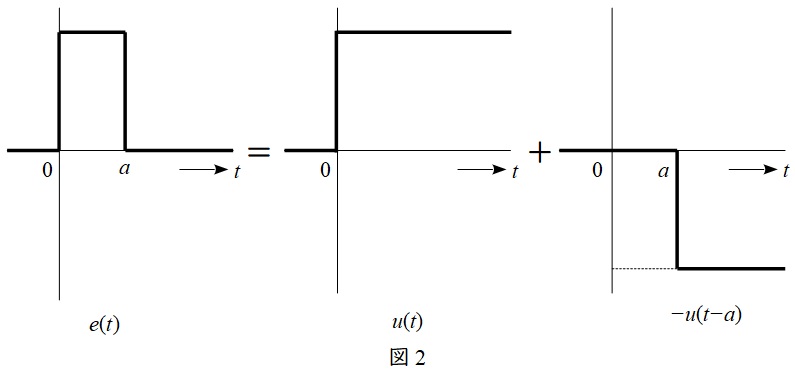
(2)解答:ホ
図2に示す通り\( \ e(t) \ \)は単位ステップ関数で表すと,
\[
\begin{eqnarray}
e\left( t\right) &=&E_{0}\left\{ u\left( t\right) -u\left( t-a\right) \right\} \\[ 5pt ]
\end{eqnarray}
\]
となるので,両辺をラプラス変換すると,
\[
\begin{eqnarray}
E\left( s\right) &=&E_{0}\left( \frac {1}{s}-\frac {1}{s}\mathrm {e}^{-as}\right) \\[ 5pt ]
&=&\frac {E_{0}}{s}\left( 1-\mathrm {e}^{-as}\right)
\end{eqnarray}
\]
と求められる。
(3)解答:ト
(2)解答式を(1)解答式に代入すると,
\[
\begin{eqnarray}
\frac {E_{0}}{s}\left( 1-\mathrm {e}^{-as}\right)&=&RI\left( s\right)+sLI\left( s\right) \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ I\left( s\right) \ \)について整理すると,
\[
\begin{eqnarray}
\frac {E_{0}}{s}\left( 1-e^{-as}\right)&=&\left( sL+R\right) I\left( s\right) \\[ 5pt ]
I\left( s\right)&=&\frac {E_{0}}{s \left( sL+R\right) }\left( 1-\mathrm {e}^{-as}\right) \\[ 5pt ]
&=&\frac {E_{0}\left( 1-\mathrm {e}^{-as}\right) }{\displaystyle Ls\left( s+\frac {R}{L}\right) } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ロ
(3)解答式について,
\[
\begin{eqnarray}
\frac {E_{0}\left( 1-\mathrm {e}^{-as}\right) }{\displaystyle Ls\left( s+\frac {R}{L}\right) } &=&\frac {E_{0}}{L}\left( \frac {A}{s}+\frac {B}{\displaystyle s+\frac {R}{L}}\right) \\[ 5pt ]
\end{eqnarray}
\]
と置き右辺を整理すると,
\[
\begin{eqnarray}
\frac {E_{0}\left( 1-\mathrm {e}^{-as}\right) }{\displaystyle Ls\left( s+\frac {R}{L}\right) }&=&\frac {\displaystyle E_{0}\left\{ A\left( s+\frac {R}{L}\right) +Bs\right\} }{\displaystyle Ls\left( s+\frac {R}{L}\right) } \\[ 5pt ]
&=&\frac {\displaystyle E_{0}\left\{ \left( A+B\right) s+A\frac {R}{L}\right\} }{\displaystyle Ls\left( s+\frac {R}{L}\right) } \\[ 5pt ]
\end{eqnarray}
\]
となる。左辺と右辺を比較すると,
\[
\begin{eqnarray}
A+B&=&0 \\[ 5pt ]
A\frac {R}{L}&=&1-\mathrm {e}^{-as} \\[ 5pt ]
\end{eqnarray}
\]
となるから,
\[
\begin{eqnarray}
A&=&\frac {L}{R}\left( 1-\mathrm {e}^{-as}\right) \\[ 5pt ]
B&=&-\frac {L}{R}\left( 1-\mathrm {e}^{-as}\right) \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって\( \ I(s) \ \)は,
\[
\begin{eqnarray}
I\left( s\right)&=&\frac {E_{0}\left( 1-\mathrm {e}^{-as}\right) }{\displaystyle Ls\left( s+\frac {R}{L}\right) } \\[ 5pt ]
&=&\frac {E_{0}}{L}\left\{ \frac {\displaystyle \frac {L}{R}\left( 1-\mathrm {e}^{-as}\right) }{s}-\frac {\displaystyle \frac {L}{R}\left( 1-\mathrm {e}^{-as}\right) }{\displaystyle s+\frac {R}{L}}\right\} \\[ 5pt ]
&=&\frac {E_{0}}{R}\left( \frac {1}{s}-\frac {1}{\displaystyle s+\frac {R}{L}}\right)\left( 1-\mathrm {e}^{-as}\right) \\[ 5pt ]
&=&\frac {E_{0}}{R}\left( \frac {1}{s}-\frac {1}{\displaystyle s+\frac {R}{L}}-\frac {1}{s}\mathrm {e}^{-as}+\frac {1}{\displaystyle s+\frac {R}{L}}\mathrm {e}^{-as}\right) \\[ 5pt ]
\end{eqnarray}
\]
となるので,両辺を逆ラプラス変換して整理すると,
\[
\begin{eqnarray}
i\left( t\right) &=&\frac {E_{0}}{R}\left[ u\left( t\right) -\mathrm {e}^{-\frac {R}{L}t}u\left( t\right) -u\left( t-a\right) +\mathrm {e}^{-\frac {R}{L}\left( t-a\right) }u\left( t-a\right)\right] \\[ 5pt ]
&=&\frac {E_{0}}{R}\left[ \left( 1-\mathrm {e}^{-\frac {R}{L}t}\right) u\left( t\right) -\left( 1-\mathrm {e}^{-\frac {R}{L}\left( t-a\right) }\right) u\left( t-a\right) \right] \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:カ
(4)解答式に各値を代入すると,
\[
\begin{eqnarray}
i\left( t\right) &=&\frac {10}{1}\left[ \left(1-\mathrm {e}^{-\frac {1}{0.1}t}\right)u\left( t\right) -\left( 1-\mathrm {e}^{-\frac {1}{0.1}\left( t-1\right) }\right) u\left( t-1\right) \right] \\[ 5pt ]
&=&10\left[ \left(1-\mathrm {e}^{-10t}\right) u\left( t\right) -\left( 1-\mathrm {e}^{-10\left( t-1\right) }\right) u\left( t-1\right) \right] \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ 1 \ \mathrm {[s]} \ \)後の電流値\( \ i\left( 1\right) \ \)は,
\[
\begin{eqnarray}
i\left( 1\right) &=&10\times \left[ \left(1-\mathrm {e}^{-10\times 1}\right) \times 1 -\left( 1-\mathrm {e}^{-10\left( 1-1\right) }\right) \times u\left( 1-1\right) \right] \\[ 5pt ]
&=&10\times \left[ (1-\mathrm {e}^{-10}) -0\right] \\[ 5pt ]
&≒& 10 \\[ 5pt ]
\end{eqnarray}
\]
であり,初期電流は零であるから,正しい波形は(カ)となる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん