《理論》〈電気回路〉[H24:問3]分布定数回路を用いた無損失線路の計算に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，分布定数回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまるものを解答群の中から選びなさい。

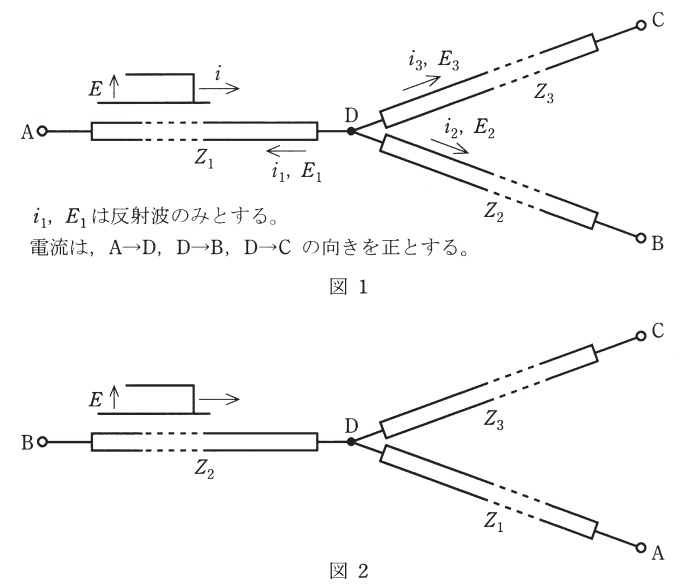
図のように，特性インピーダンスがそれぞれ$ \ Z_{1} \ $，$ \ Z_{2} \ $と$ \ Z_{3} \ $の$ \ 3 \ $本の無損失線路が接続されている。$ \ Z_{1} \ $と$ \ Z_{2} \ $，$ \ Z_{3} \ $の関係を求めたい。線路間に電気的・磁気的結合はなく，また，$ \ \mathrm {A} \ $，$ \ \mathrm {B} \ $，$ \ \mathrm {C} \ $それぞれの端子では反射がないものとする。

$ \ \mathrm {A} \ $，$ \ \mathrm {B} \ $それぞれの端子から接続点$ \ \mathrm {D} \ $に向かって波頭が階段状で波高値$ \ E \ $の電圧波が進入したとき，以下の現象が見られた。

(a)　図1のように$ \ \mathrm {A} \ $端子のみから電圧波が進入したとき，接続点$ \ \mathrm {D} \ $で反射が生じた。

(b)　図2のように$ \ \mathrm {B} \ $端子のみから電圧波が進入したとき，接続点$ \ \mathrm {D} \ $では反射が生じなかった。

現象(a)に対して，$ \ \mathrm {A} \ $端子からの入射波による電流$ \ i \ $，接続点$ \ \mathrm {D} \ $での反射により生じる電圧$ \ E_{1} \ $，電流$ \ i_{1} \ $，また，$ \ Z_{2} \ $側，$ \ Z_{3} \ $側への透過波による電圧$ \ E_{2} \ $，電流$ \ i_{2} \ $，電圧$ \ E_{3} \ $，電流$ \ i_{3} \ $を図のようにとる。電流は入射波が接続点$ \ \mathrm {D} \ $に向かって進行する方向及び透過波が接続点$ \ \mathrm {D} \ $から離れる方向を正とする。

接続点$ \ \mathrm {D} \ $の電圧，電流の関係はそれぞれ次式で表される。
\[
\begin{eqnarray}
&\left.
\begin{array}{l}
& E+E_{1} = E_{2}= E_{3} \\[ 5pt ] & i+i_{1} = i_{2}+ i_{3} \\[ 5pt ] \end{array}
\right\} \ 　・・・・・・・・・・　①
\end{eqnarray}
\] ここで，$ \ \displaystyle Y_{1}=\frac {1}{Z_{1}} \ $，$ \ \displaystyle Y_{2}=\frac {1}{Z_{2}} \ $，$ \ \displaystyle Y_{3}=\frac {1}{Z_{3}} \ $とおき，それらを用いて，$ \ E_{1} \ $，$ \ E_{2} \ $と$ \ E \ $の関係を表すと，次のようになる。
\[
\begin{eqnarray}
&\left.
\begin{array}{l}
& E_{1} = \ \fbox {　（１）　} \ \times E \\[ 5pt ] & E_{2} = \ \fbox {　（２）　} \ \times E \\[ 5pt ] \end{array}
\right\}　・・・・・・・・・・　②
\end{eqnarray}
\] 次に現象(b)について考える。接続点$ \ \mathrm {D} \ $で反射が生じないことから，$ \ Y_{2} \ $は$ \ Y_{1} \ $と$ \ Y_{3} \ $を用いると次式で表される。
\[
\begin{eqnarray}
Y_{2} &=& \ \fbox {　（３）　}　・・・・・・・・・・・・・・・・　③ \\[ 5pt ] \end{eqnarray}
\] 現象(a)において反射が生じたときの接続点$ \ \mathrm {D} \ $の電位が$ \ \displaystyle \frac {2}{3}E \ $であったとき，$ \ Z_{2} \ $，$ \ Z_{3} \ $と$ \ Z_{1} \ $の関係は次のようになる。
\[
\begin{eqnarray}
&\left.
\begin{array}{l}
& Z_{2} = \ \fbox {　（４）　} \\[ 5pt ] & Z_{3} = \ \fbox {　（５）　} \\[ 5pt ] \end{array}
\right\}　・・・・・・・・・・・・・　④
\end{eqnarray}
\]

〔問3の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {1}{2}Z_{1}　　　　　&（ロ）&　\frac {Y_{1}+Y_{3}}{Y_{1}Y_{3}}　　　　　&（ハ）&　2Z_{1} \\[ 5pt ] &（ニ）&　\frac {Y_{1}+Y_{2}+Y_{3}}{Y_{1}-Y_{2}-Y_{3}}　　　　　&（ホ）&　\frac {2Y_{1}}{Y_{1}+Y_{2}+Y_{3}}　　　　　&（ヘ）&　\frac {3}{2}Z_{1} \\[ 5pt ] &（ト）&　\frac {Y_{1}Y_{3}}{Y_{1}+Y_{3}}　　　　　&（チ）&　\frac {2Y_{1}}{Y_{1}-Y_{2}-Y_{3}}　　　　　&（リ）&　Y_{1}+Y_{3} \\[ 5pt ] &（ヌ）&　\frac {1}{\sqrt {2}}Z_{1}　　　　　&（ル）&　\frac {Y_{1}-Y_{2}-Y_{3}}{Y_{1}+Y_{2}+Y_{3}}　　　　　&（ヲ）&　3Z_{1} \\[ 5pt ] &（ワ）&　\frac {2Y_{2}Y_{3}}{Y_{1}Y_{2}+Y_{2}Y_{3}+Y_{3}Y_{1}}　　　　　&（カ）&　\frac {2}{3}Z_{1}　　　　　&（ヨ）&　\frac {Y_{2}Y_{3}-Y_{1}\left( Y_{2}+Y_{3}\right) }{Y_{1}Y_{2}+Y_{2}Y_{3}+Y_{3}Y_{1}} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

分布定数回路に関する問題です。
$ \ 2 \ $種まではあまり出題されない分布定数回路ですが， $ \ 1 \ $種では比較的出題される内容となっています。解き方はパターン化されているので，過去問を何問か繰り返すことでマスターできるようになるかと思います。

1.分布定数回路における接続点での関係式
図3のような，特性インピーダンスが$ \ Z_{1} \ $及び$ \ Z_{2} \ $の非常に長い無損失線路が接続されているときの接続点での関係式を考えます。
図の左側から波高値$ \ E \ $の電圧波が進入すると，接続点で一部の電圧が反射し，残りの電圧が透過します。このとき，入射波による電流を$ \ i \ $，反射波により生じる電圧及び電流を$ \ E_{1} \ $及び$ \ i_{1} \ $，透過波により生じる電圧及び電流を$ \ E_{2} \ $及び$ \ i_{2} \ $とし，いずれの電流も右向きに流れる電流を正とすると，以下の電圧と電流の関係式が成り立ちます。
\[
\begin{eqnarray}
E +E_{1}&=&E_{2} \\[ 5pt ] i +i_{1}&=&i_{2} \\[ 5pt ] \end{eqnarray}
\] また，各電圧と電流には，
\[
\begin{eqnarray}
E&=&Z_{1}i \\[ 5pt ] E_{1}&=&-Z_{1}i_{1} \\[ 5pt ] E_{2}&=&Z_{2}i_{2} \\[ 5pt ] \end{eqnarray}
\] の関係が成立します。

※　右向きを正とするので，電流$ \ i_{1} \ $が負の値になることに注意しましょう。

【解答】

(1)解答：ル
入射波，反射波，透過波のそれぞれにおける関係式は，ワンポイント解説「1.分布定数回路における接続点での関係式」の通り，
\[
\begin{eqnarray}
i&=&\frac {E}{Z_{1}} \\[ 5pt ] &=&Y_{1}E \\[ 5pt ] i_{1}&=&-\frac {E_{1}}{Z_{1}} \\[ 5pt ] &=&-Y_{1}E_{1} \\[ 5pt ] i_{2}&=&\frac {E_{2}}{Z_{2}} \\[ 5pt ] &=&Y_{2}E_{2} \\[ 5pt ] i_{3}&=&\frac {E_{3}}{Z_{3}} \\[ 5pt ] &=&Y_{3}E_{3} \\[ 5pt ] \end{eqnarray}
\] であるから，これを①の関係式に代入し整理すると，
\[
\begin{eqnarray}
i+i_{1}&=&i_{2}+ i_{3} \\[ 5pt ] Y_{1}E-Y_{1}E_{1}&=&Y_{2}E_{2}+ Y_{3}E_{3} \\[ 5pt ] &=&Y_{2}\left( E+E_{1}\right) + Y_{3}\left( E+E_{1}\right) \\[ 5pt ] &=&\left( Y_{2}+Y_{3}\right) \left( E+E_{1}\right) \\[ 5pt ] &=&\left( Y_{2}+Y_{3}\right) E+\left( Y_{2}+Y_{3}\right) E_{1} \\[ 5pt ] Y_{1}E_{1}+\left( Y_{2}+Y_{3}\right) E_{1}&=&Y_{1}E-\left( Y_{2}+Y_{3}\right) E \\[ 5pt ] \left( Y_{1}+Y_{2}+Y_{3}\right) E_{1}&=&\left( Y_{1}-Y_{2}-Y_{3}\right) E \\[ 5pt ] E_{1}&=&\frac {Y_{1}-Y_{2}-Y_{3}}{Y_{1}+Y_{2}+Y_{3}} E \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ホ
①式及び(1)解答式より，
\[
\begin{eqnarray}
E_{2}&=&E +E_{1} \\[ 5pt ] &=&E +\frac {Y_{1}-Y_{2}-Y_{3}}{Y_{1}+Y_{2}+Y_{3}} E \\[ 5pt ] &=&\frac {Y_{1}+Y_{2}+Y_{3}}{Y_{1}+Y_{2}+Y_{3}}E +\frac {Y_{1}-Y_{2}-Y_{3}}{Y_{1}+Y_{2}+Y_{3}} E \\[ 5pt ] &=&\frac {2Y_{1}}{Y_{1}+Y_{2}+Y_{3}}E \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：リ
図2において，反射波を生じないときの各関係式は，(1)の解答式の$ \ Y_{1} \ $と$ \ Y_{2} \ $を入れ替えた式であるので，
\[
\begin{eqnarray}
\frac {Y_{2}-Y_{1}-Y_{3}}{Y_{2}+Y_{1}+Y_{3}} E&=&0 \\[ 5pt ] Y_{2}-Y_{1}-Y_{3}&=&0 \\[ 5pt ] Y_{2}&=&Y_{1}+Y_{3} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：カ
題意より，接続点$ \ \mathrm {D} \ $の電位が$ \ \displaystyle \frac {2}{3}E \ $，すなわち$ \ \displaystyle E_{2}= \frac {2}{3}E \ $であるから，
\[
\begin{eqnarray}
E +E_{1}&=&E_{2} \\[ 5pt ] E +E_{1}&=&\frac {2}{3}E \\[ 5pt ] E_{1}&=&-\frac {1}{3}E \\[ 5pt ] \end{eqnarray}
\] となる。これを(1)の解答式に代入すると，
\[
\begin{eqnarray}
-\frac {1}{3}E&=&\frac {Y_{1}-Y_{2}-Y_{3}}{Y_{1}+Y_{2}+Y_{3}} E \\[ 5pt ] -\frac {1}{3}&=&\frac {Y_{1}-Y_{2}-Y_{3}}{Y_{1}+Y_{2}+Y_{3}} \\[ 5pt ] \end{eqnarray}
\] となり，(3)解答式より，$ \ Y_{3}=Y_{2}-Y_{1} \ $の関係があるので，
\[
\begin{eqnarray}
-\frac {1}{3}&=&\frac {Y_{1}-Y_{2}-\left( Y_{2}-Y_{1}\right) }{Y_{1}+Y_{2}+\left( Y_{2}-Y_{1}\right)} \\[ 5pt ] &=&\frac {2Y_{1}-2Y_{2}}{2Y_{2}} \\[ 5pt ] &=&\frac {Y_{1}-Y_{2}}{Y_{2}} \\[ 5pt ] -Y_{2}&=&3\left( Y_{1}-Y_{2}\right) \\[ 5pt ] &=&3Y_{1}-3Y_{2} \\[ 5pt ] 2Y_{2}&=&3Y_{1} \\[ 5pt ] \frac {2}{Z_{2}}&=&\frac {3}{Z_{1}} \\[ 5pt ] Z_{2}&=&\frac {2}{3}Z_{1} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ハ
$ \ Y_{3}=Y_{2}-Y_{1} \ $の関係より，
\[
\begin{eqnarray}
\frac {1}{Z_{3}}&=&\frac {1}{Z_{2}}-\frac {1}{Z_{1}} \\[ 5pt ] &=&\frac {1}{\displaystyle \frac {2}{3}Z_{1}}-\frac {1}{Z_{1}} \\[ 5pt ] &=&\frac {3}{2Z_{1}}-\frac {1}{Z_{1}} \\[ 5pt ] &=&\frac {1}{2Z_{1}} \\[ 5pt ] Z_{3}&=&2Z_{1} \\[ 5pt ] \end{eqnarray}
\] と求められる。