《理論》〈電子理論〉[H30:問4] 真空中の電界下で運動する単一電子による電流に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，真空中の電界下で運動する単一電子による電流に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。なお，電子の質量を$ \ m_{0} \ $，電荷量を$ \ -e \ $$( \ e＞0 \ )$とする。

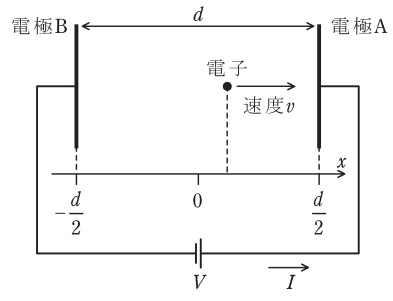
図のように，間隔$ \ d \ $で配置した平行板電極$ \ \mathrm {A} \ $，$ \ \mathrm {B} \ $間に一定の電圧$ \ V \ $$( \ V＞0 \ $とする$)$が印加されている。また，電極に垂直な座標軸$ \ x \ $を図に示す方向に定め，電極間の中点を$ \ x=0 \ $と定める。ただし，電極間に生じる電界は電極に垂直で一様とみなしてよい。時刻$ \ t=0 \ $において，一個の電子が位置$ \ x=0 \ $に静止しているものとする。時刻$ \ t＞0 \ $における電子の位置を$ \ x \ $$( \ \displaystyle x＜\frac {d}{2} \ )$とし，電界から受ける力を$ \ d \ $，$ \ V \ $等で表すと，ニュートンの運動方程式から微分方程式$ \ \displaystyle \frac {\mathrm {d}^{2}x}{\mathrm {d}t^{2}}=\fbox {　（１）　} \ $が得られる。初期条件を用いてこれを解くことにより，電子の速度$ \ \displaystyle v=\frac {\mathrm {d}x}{\mathrm {d}t} \ $は，時間$ \ t \ $の関数として$ \ v=\fbox {　（２）　} \ $と表され，位置$ \ x \ $の関数として$ \ v=\fbox {　（３）　} \ $と表される。

電子が速度$ \ v \ $で運動しているとき，微小時間$ \ \Delta t \ $の間に電界から得るエネルギーは，電子が電界から受けている力と$ \ \Delta t \ $の間に移動する距離とを乗じて，$ \ \fbox {　（４）　} \ $である。一方，このエネルギーは，電圧$ \ V \ $の直流電源から微小時間$ \ \Delta t \ $の間に電流$ \ I \ $が流れ出ることにより供給されることから，電流$ \ I \ $を$ \ d \ $，$ \ v \ $等で表すと$ \ \fbox {　（５）　} \ $と表される。

〔問4の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {V}{m_{0}d}\sqrt {2ex}　　　&（ロ）&　\frac {2eV}{m_{0}d}t　　　&（ハ）&　eVv\Delta t \\[ 5pt ] &（ニ）&　\frac {eV}{m_{0}d}　　　&（ホ）&　\frac {e}{dv}　　&（ヘ）&　\frac {V}{d}\sqrt {\frac {2e}{m_{0}}x} \\[ 5pt ] &（ト）&　\frac {e}{d}v　　　&（チ）&　\frac {eV}{d}v\Delta t　　　&（リ）&　\frac {V}{m_{0}d}t \\[ 5pt ] &（ヌ）&　\frac {2eV}{m_{0}d}　　　&（ル）&　\frac {eV}{m_{0}d}t　　　&（ヲ）&　\frac {eV}{d}\Delta t \\[ 5pt ] &（ワ）&　\sqrt {\frac {2eV}{m_{0}d}x}　　　&（カ）&　\frac {ed}{v}　　　&（ヨ）&　\frac {eV}{2m_{0}d} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

真空電子理論に関する出題です。(4)，(5)の変形に若干手間取るかもしれませんが，公式はそれほど難しい公式は使用しませんので，確実に導き出せるようにしましょう。

1.運動方程式と静電力の関係
質量$ \ m \ $の電子に力$ \ F \ $が加わった時の加速度$ \ a \ $には，
\[
\begin{eqnarray}
F &=& ma \\[ 5pt ] \end{eqnarray}
\] の関係があり，これを運動方程式と言います。
電界$ \ E \ $が電子に加わった時，静電力$ \ F \ $は，
\[
\begin{eqnarray}
F &=& eE \\[ 5pt ] \end{eqnarray}
\] であるので，静電力が加わった時の加速度は，
\[
\begin{eqnarray}
ma &=& eE \\[ 5pt ] a &=& \frac {eE}{m} \\[ 5pt ] \end{eqnarray}
\] の関係があります。

【解答】

(1)解答：ニ
ワンポイント解説「1.運動方程式と静電力の関係」より，
\[
\begin{eqnarray}
F = m_{0}\frac {\mathrm {d}^{2}x}{\mathrm {d}t^{2}} &=&eE \\[ 5pt ] \end{eqnarray}
\] であり，$ \ \displaystyle E = \frac {V}{d} \ $であるから，
\[
\begin{eqnarray}
m_{0}\frac {\mathrm {d}^{2}x}{\mathrm {d}t^{2}} &=&\frac {eV}{d} \\[ 5pt ] \frac {\mathrm {d}^{2}x}{\mathrm {d}t^{2}} &=&\frac {eV}{m_{0}d} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ル
(1)の解答式の両辺を$ \ t \ $で積分すると，
\[
\begin{eqnarray}
\frac {\mathrm {d}x}{\mathrm {d}t} &=&\frac {eV}{m_{0}d}t+C　(Cは積分定数) \\[ 5pt ] \end{eqnarray}
\] となる。最初電子は静止しているので，$ \ C=0 \ $であるから，
\[
\begin{eqnarray}
\frac {\mathrm {d}x}{\mathrm {d}t} &=&\frac {eV}{m_{0}d}t \\[ 5pt ] v &=&\frac {eV}{m_{0}d}t \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ワ
$ \ t \ $秒後の電子の位置$ \ x \ $は，
\[
\begin{eqnarray}
x &=&\frac {1}{2}\frac {\mathrm {d}^{2}x}{\mathrm {d}t^{2}}t^{2} \\[ 5pt ] \end{eqnarray}
\] であり，(2)の解答式より，
\[
\begin{eqnarray}
t &=&\frac {m_{0}dv}{eV} \\[ 5pt ] \end{eqnarray}
\] であるから，
\[
\begin{eqnarray}
x &=&\frac {1}{2}\frac {\mathrm {d}^{2}x}{\mathrm {d}t^{2}}t^{2} \\[ 5pt ] &=&\frac {1}{2}\frac {eV}{m_{0}d}\left( \frac {m_{0}dv}{eV}\right) ^{2} \\[ 5pt ] &=&\frac {m_{0}d}{2eV}v ^{2} \\[ 5pt ] \end{eqnarray}
\] となり，$ \ v \ $について整理すると，
\[
\begin{eqnarray}
v ^{2} &=&\frac {2eV}{m_{0}d}x \\[ 5pt ] v&=&\sqrt {\frac {2eV}{m_{0}d}x} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：チ
電子が電界から受けている力$ \ F \ $は，
\[
\begin{eqnarray}
F &=&eE \\[ 5pt ] &=&\frac {eV}{d} \\[ 5pt ] \end{eqnarray}
\] であり，$ \ \Delta t \ $の間に移動する距離$ \ \Delta x \ $は，
\[
\begin{eqnarray}
\Delta x &=&v \Delta t \\[ 5pt ] \end{eqnarray}
\] であるから，これらを乗じると，電子が得るエネルギー$ \ \Delta W \ $は，
\[
\begin{eqnarray}
\Delta W &=&F \Delta x \\[ 5pt ] &=&\frac {eV}{d}v \Delta t \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ト
電源から供給されるエネルギーは電力$ \ P \ $と$ \ \Delta t \ $の積であるから，
\[
\begin{eqnarray}
P \Delta t &=&VI \Delta t \\[ 5pt ] \end{eqnarray}
\] となり，これが電子が得るエネルギーと等しいので，
\[
\begin{eqnarray}
VI \Delta t &=&\frac {eV}{d}v \Delta t \\[ 5pt ] I &=&\frac {e}{d}v \\[ 5pt ] \end{eqnarray}
\] と求められる。