《理論》〈電気回路〉[R01:問6]電気回路の過渡現象に関する計算問題

1 【問題】
2 【ワンポイント解説】
- 2.1 【関連する「電気の神髄」記事】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，電気回路の過渡現象に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

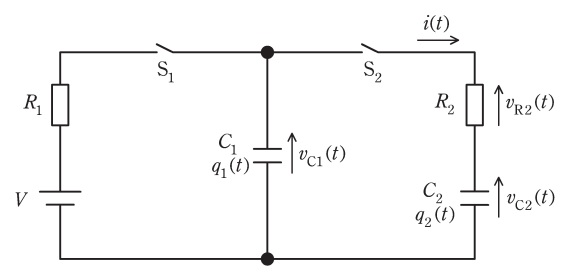
図の回路は，時刻$ \ t＜0 \ $ではスイッチ$ \ \mathrm {S_{1}} \ $は閉じており，スイッチ$ \ \mathrm {S_{2}} \ $は開いている。また，回路は定常状態にあり，キャパシタ$ \ \mathrm {C_{2}} \ $の電荷は零である。この回路において，時刻$ \ t=0 \ $でスイッチ$ \ \mathrm {S_{1}} \ $を開き，同時にスイッチ$ \ \mathrm {S_{2}} \ $を閉じるものとする。

キャパシタ$ \ C_{1} \ $，$ \ C_{2} \ $の電荷をそれぞれ$ \ q_{1}(t) \ $，$ \ q_{2}(t) \ $とすれば，時刻$ \ t≧0 \ $における$ \ q_{1}(t) \ $，$ \ q_{2}(t) \ $には次式が成り立つ。
\[
\begin{eqnarray}
q_{1}(t) + q_{2}(t) &=& \ \fbox {　（１）　} \ 　・・・・・・・・・・　① \\[ 5pt ] \end{eqnarray}
\] 抵抗$ \ R_{2} \ $の電圧を$ \ v_{\mathrm {R2}}(t) \ $とし，キャパシタ$ \ C_{1} \ $，$ \ C_{2} \ $の電圧をそれぞれ$ \ v_{\mathrm {C1}}(t) \ $，$ \ v_{\mathrm {C2}}(t) \ $とすれば，時刻$ \ t≧0 \ $においては，キルヒホッフの電圧則に従う次式が成り立つ。
\[
\begin{eqnarray}
v_{\mathrm {R2}}(t)-v_{\mathrm {C1}}(t) + v_{\mathrm {C2}}(t) &=& 0　・・・・・・・・・・　② \\[ 5pt ] \end{eqnarray}
\] ここで，$ \ v_{\mathrm {C1}}(t) = \ \fbox {　（２）　} \ $，$ \ v_{\mathrm {C2}}(t) = \ \fbox {　（３）　} \ $，$ \ i(t) =\frac {\mathrm {d}q_{2}(t)}{\mathrm {d}t} \ $，及び①式より，②式はキャパシタ$ \ C_{2} \ $の電荷$ \ q_{2}(t) \ $を用いて次式のように表現できる。
\[
\begin{eqnarray}
R_{2}\frac {\mathrm {d}q_{2}(t)}{\mathrm {d}t}+\left( \ \fbox {　（４）　} \ \right) q_{2}(t) -V &=& 0　・・・・・・・・・・　② \\[ 5pt ] \end{eqnarray}
\] 回路の初期条件を考慮して，③式の微分方程式を解けば，
\[
\begin{eqnarray}
q_{2}(t) &=& \ \fbox {　（５）　} \ \left( 1-\mathrm {e}^{-t / T}\right) \\[ 5pt ] \end{eqnarray}
\] を得る。ただし，時定数$ \ T = \ \fbox {　（６）　} \ $である。

時刻$ \ t = \infty \ $の定常状態においては，キャパシタ$ \ C_{1} \ $の電圧$ \ v_{\mathrm {C1\infty }} \ $とキャパシタ$ \ C_{2} \ $の電圧$ \ v_{\mathrm {C2\infty }} \ $は等しく，$ \ v_{\mathrm {C1\infty }}=v_{\mathrm {C2\infty }}= \ \fbox {　（７）　} \ $となる。

時刻$ \ t＜0 \ $において，二つのキャパシタ$ \ C_{1} \ $及び$ \ C_{2} \ $に蓄積されていた総エネルギーは$ \ \fbox {　（８）　} \ $である。この総エネルギーの一部は時刻$ \ t≧0 \ $において回路の$ \ \fbox {　（９）　} \ $で消費され，時刻$ \ t = \infty \ $において二つのキャパシタ$ \ C_{1} \ $及び$ \ C_{2} \ $に蓄積されている総エネルギーは，時刻$ \ t＜0 \ $において蓄積されていた総エネルギーに比べて$ \ \fbox {　（１０）　} \ $だけ減少する。

〔問6の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {C_{1}C_{2}}{C_{1}+C_{2}}R_{1}　　　　　&（ロ）&　\frac {C_{1}-C_{2}}{C_{1}C_{2}}　　　　　&（ハ）&　C_{2}V \\[ 5pt ] &（ニ）&　\frac {C_{1}C_{2}}{C_{1}+C_{2}}V　　　　　&（ホ）&　\frac {1}{2}\frac {C_{1}C_{2}}{C_{1}+C_{2}}V^{2}　　　　　&（ヘ）&　R_{1} \\[ 5pt ] &（ト）&　C_{1}V　　　　　&（チ）&　0　　　　　&（リ）&　\frac {C_{1}C_{2}}{C_{1}+C_{2}}V^{2} \\[ 5pt ] &（ヌ）&　\frac {1}{2}C_{1}V^{2}　　　　　&（ル）&　R_{2}　　　　　&（ヲ）&　\frac {C_{1}+C_{2}}{C_{1}C_{2}}V \\[ 5pt ] &（ワ）&　\frac {C_{1}}{C_{1}+C_{2}}V　　　　　&（カ）&　\frac {1}{2}C_{2}V^{2}　　　　　&（ヨ）&　\frac {q_{1}(t)}{C_{1}} \\[ 5pt ] &（タ）&　\frac {C_{1}+C_{2}}{C_{1}C_{2}}　　　　　&（レ）&　\frac {C_{1}C_{2}}{C_{1}+C_{2}}R_{2}　　　　　&（ソ）&　\frac {C_{2}}{C_{1}+C_{2}}V \\[ 5pt ] &（ツ）&　V　　　　　&（ネ）&　\frac {q_{2}(t)}{C_{2}}　　　　　&& \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

難易度はそれほど高くないですが，空欄数が多いので時間との勝負になると思います。似たような選択肢も多いので間違えないように迅速かつ慎重に解く必要があります。

1.過渡現象における$ \ RLC \ $それぞれの電圧
線路に流れる電流を$ \ i \ $とし，抵抗$ \ R \ $の電圧$ \ V_{\mathrm{R}} \ $，リアクトル$ \ L \ $の電圧$ \ V_{\mathrm{L}} \ $，コンデンサ$ \ C \ $の電圧$ \ V_{\mathrm{C}} \ $とすると，
\[
\begin{eqnarray}
V_{\mathrm{R}} &=& Ri \\[ 5pt ] V_{\mathrm{L}} &=& L\frac {\mathrm {d}i}{\mathrm {d}t} \\[ 5pt ] V_{\mathrm{C}} &=& \frac {1}{C}\int i \mathrm {d}t =\frac {q}{C}\\[ 5pt ] \end{eqnarray}
\] となります。

2.過渡現象における定常解と過渡解
ⅰ．定常解を$ \ i_{\mathrm {s}} \ $，過渡解を$ \ i_{\mathrm {t}} \ $とすると，電流値$ \ i \ $は$ \ i=i_{\mathrm {s}}+i_{\mathrm {t}} \ $となります。
ⅱ．定常解は電流の時間変化のない状態すなわち$ \ \displaystyle \frac {\mathrm {d}i_{\mathrm {s}}}{\mathrm {d}t}=0 \ $とした時の解です。
ⅲ．過渡解はスイッチを入れた直後の解です。

3.自然対数の微分積分
①自然対数の微分
\[
\begin{eqnarray}
\frac {\mathrm {d}}{\mathrm {d}x} \left ( \ln {x} \right) &=&\frac {1}{x} \\[ 5pt ]　
\end{eqnarray}
\] ②自然対数の積分
\[
\begin{eqnarray}
\int \frac {1}{x} \mathrm {d}x&=&\ln {x} + C \left( Cは積分定数\right) \\[ 5pt ] \end{eqnarray}
\] \[
\begin{eqnarray}
\ln {x} &=&-\alpha t +C \left( Cは積分定数\right)の時，　x=Ae^{-\alpha t} \left( A=e^{C}\right)となります。 \\[ 5pt ] \end{eqnarray}
\]

【関連する「電気の神髄」記事】

　　RC並列回路の過渡現象（直流回路）

【解答】

(1)解答：ト
$ \ t＜0 \ $ではスイッチ$ \ \mathrm {S_{1}} \ $は閉じており，スイッチ$ \ \mathrm {S_{2}} \ $は開いていたので，$ \ t=0 \ $でキャパシタ$ \ C_{\mathrm {1}} \ $に蓄えらえる電荷$ \ q_{1}(0) \ $は，
\[
\begin{eqnarray}
q_{1}(0) &=&C_{1}V \\[ 5pt ] \end{eqnarray}
\] となる。その後，$ \ t=0 \ $でスイッチ$ \ \mathrm {S_{1}} \ $を開き，同時にスイッチ$ \ \mathrm {S_{2}} \ $を閉じたので，その後電荷の移動はあるものの，キャパシタ$ \ C_{1} \ $及び$ \ C_{2} \ $に蓄えられる電荷の総量は変わらない。したがって，
\[
\begin{eqnarray}
q_{1}(t) + q_{2}(t) &=& C_{1}V \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ヨ
ワンポイント解説「1.過渡現象における$ \ RLC \ $それぞれの電圧」の通り，$ \ \displaystyle v_{\mathrm {C1}}(t) = \frac {q_{1}(t)}{C_{1}} \ $となります。

(3)解答：ネ
ワンポイント解説「1.過渡現象における$ \ RLC \ $それぞれの電圧」の通り，$ \ \displaystyle v_{\mathrm {C2}}(t) = \frac {q_{2}(t)}{C_{2}} \ $となります。

(4)解答：タ
(2)，(3)より②式は，
\[
\begin{eqnarray}
v_{\mathrm {R2}}(t)-v_{\mathrm {C1}}(t) + v_{\mathrm {C2}}(t) &=& 0 \\[ 5pt ] R_{2}\frac {\mathrm {d}q_{2}(t)}{\mathrm {d}t}-\frac {q_{1}(t)}{C_{1}}+ \frac {q_{2}(t)}{C_{2}} &=& 0 \\[ 5pt ] \end{eqnarray}
\] となる。ここで，①より，$ \ q_{1}(t) = C_{1}V- q_{2}(t) \ $であるから，
\[
\begin{eqnarray}
R_{2}\frac {\mathrm {d}q_{2}(t)}{\mathrm {d}t}-\frac { C_{1}V- q_{2}(t)}{C_{1}}+ \frac {q_{2}(t)}{C_{2}} &=& 0 \\[ 5pt ] R_{2}\frac {\mathrm {d}q_{2}(t)}{\mathrm {d}t}-V+\frac { q_{2}(t)}{C_{1}}+ \frac {q_{2}(t)}{C_{2}} &=& 0 \\[ 5pt ] R_{2}\frac {\mathrm {d}q_{2}(t)}{\mathrm {d}t}+\frac {C_{1}+C_{2}}{C_{1}C_{2}} q_{2}(t) -V &=& 0 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ニ
③式は，
\[
\begin{eqnarray}
R_{2}\frac {\mathrm {d}q_{2}(t)}{\mathrm {d}t}+\frac {C_{1}+C_{2}}{C_{1}C_{2}} q_{2}(t) &=& V \\[ 5pt ] \end{eqnarray}
\] となるので，定常解$ \ q_{\mathrm {2s}} \ $は，$ \ \displaystyle \frac {\mathrm {d}q_{2}(t)}{\mathrm {d}t}=0 \ $とすると，
\[
\begin{eqnarray}
\frac {C_{1}+C_{2}}{C_{1}C_{2}} q_{\mathrm {2s}} &=& V \\[ 5pt ] q_{\mathrm {2s}} &=& \frac {C_{1}C_{2}}{C_{1}+C_{2}}V \\[ 5pt ] \end{eqnarray}
\] となる。また，過渡解$ \ q_{\mathrm {2t}} \ $は，$ \ V=0 \ $とすると，
\[
\begin{eqnarray}
R_{2}\frac {\mathrm {d} q_{\mathrm {2t}}}{\mathrm {d}t}+\frac {C_{1}+C_{2}}{C_{1}C_{2}} q_{\mathrm {2t}} &=& 0 \\[ 5pt ] R_{2}\frac {\mathrm {d} q_{\mathrm {2t}}}{\mathrm {d}t} &=& -\frac {C_{1}+C_{2}}{C_{1}C_{2}} q_{\mathrm {2t}} \\[ 5pt ] \frac {1}{q_{\mathrm {2t}}}\mathrm {d} q_{\mathrm {2t}} &=&-\frac {C_{1}+C_{2}}{R_{2}C_{1}C_{2}}\mathrm {d}t \\[ 5pt ] \end{eqnarray}
\] と整理でき，両辺積分すると，
\[
\begin{eqnarray}
q_{\mathrm {2t}} &=&A\mathrm {e}^{-\frac {C_{1}+C_{2}}{R_{2}C_{1}C_{2}}t} \left( Aは積分定数\right) \\[ 5pt ] \end{eqnarray}
\] となる。よって，一般解は，
\[
\begin{eqnarray}
q_{\mathrm {2}}(t) &=&q_{\mathrm {2s}} +q_{\mathrm {2t}} \\[ 5pt ] &=&\frac {C_{1}C_{2}}{C_{1}+C_{2}}V +A\mathrm {e}^{-\frac {C_{1}+C_{2}}{R_{2}C_{1}C_{2}}t} \\[ 5pt ] \end{eqnarray}
\] となる。題意より，$ \ t=0 \ $においてキャパシタ$ \ \mathrm {C_{2}} \ $の電荷は零であるから，
\[
\begin{eqnarray}
0&=&\frac {C_{1}C_{2}}{C_{1}+C_{2}}V +A \\[ 5pt ] A&=&-\frac {C_{1}C_{2}}{C_{1}+C_{2}}V \\[ 5pt ] \end{eqnarray}
\] となり，$ \ q_{\mathrm {2}}(t) \ $は，
\[
\begin{eqnarray}
q_{\mathrm {2}}(t) &=&\frac {C_{1}C_{2}}{C_{1}+C_{2}}V\left( 1-\mathrm {e}^{-\frac {C_{1}+C_{2}}{R_{2}C_{1}C_{2}}t}\right) \\[ 5pt ] \end{eqnarray}
\] と求められる。

(6)解答：レ
(5)の解答式より，$ \ \displaystyle T=\frac {C_{1}C_{2}}{C_{1}+C_{2}}R_{2} \ $と求められる。

(7)解答：ワ
$ \ t = \infty \ $の定常状態においては，
\[
\begin{eqnarray}
v_{\mathrm {C1\infty }}=v_{\mathrm {C2\infty }}&=&\frac {q_{\mathrm {2s}}}{C_{2}} \\[ 5pt ] &=&\frac { \displaystyle \frac {C_{1}C_{2}}{C_{1}+C_{2}}V}{C_{2}} \\[ 5pt ] &=&\frac {C_{1}}{C_{1}+C_{2}}V \\[ 5pt ] \end{eqnarray}
\] と求められる。

(8)解答：ヌ
時刻$ \ t＜0 \ $において，$ \ C_{2} \ $は電荷が零なので，蓄積されている総エネルギー$ \ W_{0} \ $は，
\[
\begin{eqnarray}
W_{0}&=&\frac {1}{2}C_{1}V^{2} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(9)解答：ル
総エネルギーの一部は電荷が$ \ C_{1} \ $から$ \ C_{2} \ $に移動する過程において，抵抗$ \ R_{2} \ $で消費される。

(10)解答：ホ
(7)解答式より，$ \ t = \infty \ $において，二つのキャパシタに蓄えられるエネルギー$ \ W_{\infty } \ $は，
\[
\begin{eqnarray}
W_{\infty }&=&\frac {1}{2}C_{1}{v_{\mathrm {C1\infty }}}^{2}+\frac {1}{2}C_{2}{v_{\mathrm {C2\infty }}}^{2} \\[ 5pt ] &=&\frac {1}{2}C_{1} \left( \frac {C_{1}}{C_{1}+C_{2}}V\right) ^{2}+\frac {1}{2}C_{2} \left( \frac {C_{1}}{C_{1}+C_{2}}V\right) ^{2} \\[ 5pt ] &=&\frac {1}{2}\left( C_{1}+C_{2}\right) \left( \frac {C_{1}}{C_{1}+C_{2}}V\right) ^{2} \\[ 5pt ] &=&\frac {1}{2} \frac {C_{1}^{2}}{C_{1}+C_{2}}V ^{2} \\[ 5pt ] \end{eqnarray}
\] となり，減少したエネルギーは，
\[
\begin{eqnarray}
W_{0}-W_{\infty }&=&\frac {1}{2}C_{1}V^{2}-\frac {1}{2} \frac {C_{1}^{2}}{C_{1}+C_{2}}V ^{2} \\[ 5pt ] &=&\frac {1}{2}C_{1}V^{2}\left( 1- \frac {C_{1}}{C_{1}+C_{2}}\right) \\[ 5pt ] &=&\frac {1}{2}\frac {C_{1}C_{2}}{C_{1}+C_{2}}V^{2} \\[ 5pt ] \end{eqnarray}
\] と求められる。