【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,回路の過渡現象に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
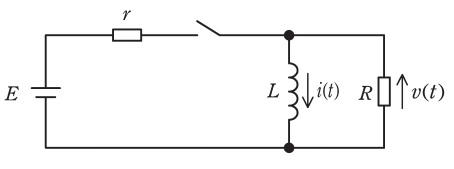
図の回路は,直流電圧源\( \ E \ \),抵抗\( \ r \ \)及び\( \ R \ \),インダクタンス\( \ L \ \)のコイルで構成されている。時刻\( \ t<0 \ \)でスイッチは開いており,コイルの磁束は零とする。\( \ t=0 \ \)でスイッチを閉じた。
\( \ t≧0 \ \)における抵抗\( \ R \ \)の電圧\( \ v\left( t \right) \ \)はコイルの電圧と等しいので,コイルの電流を\( \ i\left( t \right) \ \)とおくと,\( \ v\left( t \right) = \ \fbox { (1) } \ \)である。したがって,回路の閉路\( \ E-r-R-E \ \)の電圧平衡の式は以下の式となる。
\[
\begin{eqnarray}
E &=&r\left[ \frac {1}{R} \ \fbox { (1) } \ +i\left( t \right) \right] + \ \fbox { (1) } \ ・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
ここで,回路の時定数を\( \ \tau \ \)とすると,①式より\( \ \tau = \ \fbox { (2) } \ \)である。時定数\( \ \tau \ \)を使うと,\( \ t≧0 \ \)での抵抗\( \ R \ \)の電圧\( \ v\left( t \right) \ \)とコイルの電流\( \ i\left( t \right) \ \)の式は,それぞれ,
\[
\begin{eqnarray}
v\left( t \right) &=&v\left( 0 \right) \mathrm {e}^{-t / \tau },ただし,v\left( 0 \right) = \ \fbox { (3) } \ \\[ 5pt ]
i\left( t \right) &=&i\left( \infty \right) \left( 1- \mathrm {e}^{-t / \tau } \right) ,ただし,i\left( \infty \right) = \ \fbox { (4) } \ \\[ 5pt ]
\end{eqnarray}
\]
と表せる。
\( \ t=0 \ \)から回路が定常状態となるまでに,抵抗\( \ R \ \)が消費するエネルギーを\( \ J_{\mathrm {R}} \ \),定常状態でコイルが保有する磁気エネルギーを\( \ J_{\mathrm {L}} \ \)とおくと,
\[
\begin{eqnarray}
J_{\mathrm {R}} &=&\int _{0}^{\infty } \frac {1}{R} {v\left( t \right) }^{2} \mathrm {d}t=\frac {1}{R} {v\left( 0 \right) }^{2}\int _{0}^{\infty }\mathrm {e}^{-2t / \tau } \mathrm {d}t =\frac {1}{R} {v\left( 0 \right) }^{2}\frac {\tau }{2} \\[ 5pt ]
J_{\mathrm {L}} &=&\frac {1}{2}L{i\left( \infty \right) } ^{2} \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ J_{\mathrm {R}} \ \)と\( \ J_{\mathrm {L}} \ \)に\( \ \fbox { (2) } \ \),\( \ \fbox { (3) } \ \),\( \ \fbox { (4) } \ \)の式を代入すると,\( \ \displaystyle \frac {J_{\mathrm {R}}}{J_{\mathrm {L}}} \ \)は\( \ \fbox { (5) } \ \)となる。
〔問4の解答群〕
\[
\begin{eqnarray}
&(イ)& E &(ロ)& \frac {J_{\mathrm {R}}}{J_{\mathrm {L}}}=1 &(ハ)& \frac {J_{\mathrm {R}}}{J_{\mathrm {L}}}=\frac {R}{r} \\[ 5pt ]
&(ニ)& L\frac {R+r}{Rr} &(ホ)& \frac {E}{R} &(ヘ)& \frac {L}{r} \\[ 5pt ]
&(ト)& L\frac {\mathrm {d}}{\mathrm {d}t}i\left( t \right) &(チ)& \frac {ER}{R+r} &(リ)& \frac {E}{r} \\[ 5pt ]
&(ヌ)& \frac {L}{R} &(ル)& Li\left( t \right) &(ヲ)& \frac {1}{L}\int _{0}^{t} i\left( \theta \right) \mathrm {d}\theta \\[ 5pt ]
&(ワ)& \frac {Er}{R} &(カ)& \frac {E}{Rr}\left( R+r \right) &(ヨ)& \frac {J_{\mathrm {R}}}{J_{\mathrm {L}}}=\frac {r}{R+r} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
2種から定番となっている過渡現象に関する問題です。
2種では以前からほぼ毎年出題されていましたが,1種においても平成29年から4年連続で出題されています。今後も過渡現象は定番となっていく可能性があるので,1種と2種の過去問を習熟して確実に本番で解けるように準備しましょう。
1.過渡現象における\( \ RLC \ \)それぞれの電圧
線路に流れる電流を\( \ i \ \)とし,抵抗\( \ R \ \)の電圧\( \ V_{\mathrm{R}} \ \),リアクトル\( \ L \ \)の電圧\( \ V_{\mathrm{L}} \ \),コンデンサ\( \ C \ \)の電圧\( \ V_{\mathrm{C}} \ \)とすると,
\[
\begin{eqnarray}
V_{\mathrm{R}} &=& Ri \\[ 5pt ]
V_{\mathrm{L}} &=& L\frac {\mathrm {d}i}{\mathrm {d}t} \\[ 5pt ]
V_{\mathrm{C}} &=& \frac {1}{C}\int i \mathrm {d}t =\frac {q}{C}\\[ 5pt ]
\end{eqnarray}
\]
となります。
2.過渡現象における定常解と過渡解
ⅰ.定常解を\( \ i_{\mathrm {s}} \ \),過渡解を\( \ i_{\mathrm {t}} \ \)とすると,電流値\( \ i \ \)は\( \ i=i_{\mathrm {s}}+i_{\mathrm {t}} \ \)となります。
ⅱ.定常解は電流の時間変化のない状態すなわち\( \ \displaystyle \frac {\mathrm {d}i_{\mathrm {s}}}{\mathrm {d}t}=0 \ \)とした時の解です。
ⅲ.過渡解はスイッチを入れた直後の解です。
3.自然対数の微分積分
①自然対数の微分
\[
\begin{eqnarray}
\frac {\mathrm {d}}{\mathrm {d}x} \left ( \ln {x} \right) &=&\frac {1}{x} \\[ 5pt ]
\end{eqnarray}
\]
②自然対数の積分
\[
\begin{eqnarray}
\int \frac {1}{x} \mathrm {d}x&=&\ln {x} + C \left( Cは積分定数\right) \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
\ln {x} &=&-\alpha t +C \left( Cは積分定数\right)の時, x=Ae^{-\alpha t} \left( A=e^{C}\right)となります。 \\[ 5pt ]
\end{eqnarray}
\]
【関連する「電気の神髄」記事】
【解答】
(1)解答:ト
ワンポイント解説「1.過渡現象における\( \ RLC \ \)それぞれの電圧」の通り,\( \ v\left( t \right) \ \)はコイルの電圧と等しいから,
\[
\begin{eqnarray}
v\left( t \right) &=& L\frac {\mathrm {d}}{\mathrm {d}t}i\left( t \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ニ
(1)解答式より,回路の閉路\( \ E-r-R-E \ \)の回路方程式は,
\[
\begin{eqnarray}
E &=&r\left[ \frac {1}{R} L\frac {\mathrm {d}}{\mathrm {d}t}i\left( t \right) +i\left( t \right) \right] + L\frac {\mathrm {d}}{\mathrm {d}t}i\left( t \right) \\[ 5pt ]
E &=&\left( \frac {rL}{R} +L\right) \frac {\mathrm {d}}{\mathrm {d}t}i\left( t \right) +ri\left( t \right) \\[ 5pt ]
E &=&\frac {\left( R+r\right) L}{R} \frac {\mathrm {d}}{\mathrm {d}t}i\left( t \right) +ri\left( t \right) \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,ワンポイント解説「2.過渡現象における定常解と過渡解」の通り,上式の定常解を\( \ i_{\mathrm {s}} \ \)とすると,\( \ \displaystyle \frac {\mathrm {d}}{\mathrm {d}t}i\left( t \right) =0 \ \)であるから,
\[
\begin{eqnarray}
E &=& ri_{\mathrm {s}} \\[ 5pt ]
i_{\mathrm {s}}&=& \frac {E}{r} \\[ 5pt ]
\end{eqnarray}
\]
となり,過渡解を\( \ i_{\mathrm {t}} \ \)とすると,
\[
\begin{eqnarray}
0 &=&\frac {\left( R+r\right) L}{R} \frac {\mathrm {d}i_{\mathrm {t}}}{\mathrm {d}t} +ri_{\mathrm {t}} \\[ 5pt ]
\frac {\left( R+r\right) L}{R} \frac {\mathrm {d}i_{\mathrm {t}}}{\mathrm {d}t} &=& -ri_{\mathrm {t}} \\[ 5pt ]
\frac {1}{i_{\mathrm {t}}}\mathrm {d}i_{\mathrm {t}} &=&-\frac {Rr}{\left( R+r\right) L} \mathrm {d}t \\[ 5pt ]
\end{eqnarray}
\]
となるので,両辺積分すると,
\[
\begin{eqnarray}
\int \frac {1}{i_{\mathrm {t}}}\mathrm {d}i_{\mathrm {t}} &=&\int \left\{ -\frac {Rr}{\left( R+r\right) L}\right\} \mathrm {d}t \\[ 5pt ]
\ln i_{\mathrm {t}} &=& -\frac {Rr}{\left( R+r\right) L} t+C \left( Cは積分定数\right) \\[ 5pt ]
i_{\mathrm {t}} &=&A\mathrm {e}^{-\frac {Rr}{\left( R+r\right) L} t} \left( Aは積分定数\right) \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,一般解は,
\[
\begin{eqnarray}
i\left( t \right) &=& i_{\mathrm {s}}+i_{\mathrm {t}} \\[ 5pt ]
&=& \frac {E}{r}+A\mathrm {e}^{-\frac {Rr}{\left( R+r\right) L} t} \\[ 5pt ]
\end{eqnarray}
\]
となり,コイルに流れる電流の初期値\( \ i\left( 0 \right) =0 \ \)であるから,
\[
\begin{eqnarray}
i\left( 0 \right) &=& \frac {E}{r}+A\mathrm {e}^{-\frac {Rr}{\left( R+r\right) L} \times 0} \\[ 5pt ]
0 &=& \frac {E}{r}+A \\[ 5pt ]
A &=& -\frac {E}{r} \\[ 5pt ]
\end{eqnarray}
\]
となり,
\[
\begin{eqnarray}
i\left( t \right) &=& \frac {E}{r}-\frac {E}{r}\mathrm {e}^{-\frac {Rr}{\left( R+r\right) L} t} \\[ 5pt ]
&=& \frac {E}{r}\left\{ 1-\mathrm {e}^{-\frac {Rr}{\left( R+r\right) L} t}\right\} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。以上から,\( \ \displaystyle \tau =\frac {\left( R+r\right) L}{Rr} \ \)と求められる。
※ 試験本番では過渡解を求めた時点で正答を出せるようにしましょう。
(3)解答:チ
(1)及び(2)の解答式より,
\[
\begin{eqnarray}
v\left( t \right) &=& L\frac {\mathrm {d}}{\mathrm {d}t}i\left( t \right) \\[ 5pt ]
&=& L\frac {\mathrm {d}}{\mathrm {d}t}\left\{ \frac {E}{r}\left( 1-\mathrm {e}^{-\frac {Rr}{\left( R+r\right) L} t}\right) \right\} \\[ 5pt ]
&=& \frac {EL}{r}\frac {\mathrm {d}}{\mathrm {d}t} \left( 1-\mathrm {e}^{-\frac {Rr}{\left( R+r\right) L} t}\right) \\[ 5pt ]
&=& \frac {EL}{r}\left[ 0-\left\{ -\frac {Rr}{\left( R+r\right) L}\right\} \mathrm {e}^{-\frac {Rr}{\left( R+r\right) L} t}\right] \\[ 5pt ]
&=& \frac {ER}{R+r} \mathrm {e}^{-\frac {Rr}{\left( R+r\right) L} t} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ \displaystyle v\left( 0 \right) =\frac {ER}{R+r} \ \)と求められる。
※ 試験本番では分圧の法則から正答を導出しても大丈夫です。
(4)解答:リ
(2)解答式より,
\[
\begin{eqnarray}
i\left( \infty \right) &=& \frac {E}{r} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
※ 試験本番では,定常解\( \ i_{\mathrm {s}} \ \)を求めた時点で正答を導き出せるようにしましょう。
(5)解答:ヨ
(2)~(4)より,
\[
\begin{eqnarray}
J_{\mathrm {R}} &=&\frac {1}{R}\left( \frac {ER}{R+r} \right) ^{2}\frac {\displaystyle \frac {\left( R+r\right) L}{Rr}}{2} \\[ 5pt ]
&=&\frac {E^{2}L}{2r\left( R+r \right) } \\[ 5pt ]
J_{\mathrm {L}} &=&\frac {1}{2}L\left( \frac {E}{r} \right) ^{2} \\[ 5pt ]
&=&\frac {E^{2}L}{2r^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
\frac {J_{\mathrm {R}}}{J_{\mathrm {L}}} &=&\frac {\displaystyle \frac {E^{2}L}{2r\left( R+r \right) }}{\displaystyle \frac {E^{2}L}{2r^{2}}} \\[ 5pt ]
&=&\frac {r}{R+r} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん