【問題】
【難易度】★★★☆☆(普通)
次の文章は,三相交流回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
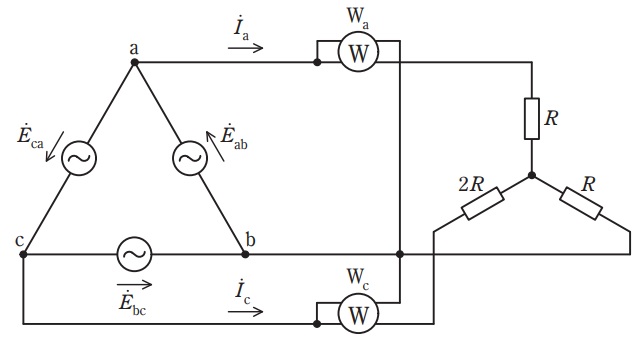
図のように,対称三相交流電源が,\( \ R \ \mathrm {[\Omega ]} \ \)及び\( \ 2R \ \mathrm {[\Omega ]} \ \)の抵抗で構成された\( \ \mathrm {Y} \ \)形負荷に接続されている。線間電圧は\( \ \left| {\dot E}_{\mathrm {ab}} \right| =\left| {\dot E}_{\mathrm {bc}} \right| =\left| {\dot E}_{\mathrm {ca}} \right| = E \ \mathrm {[V]} \ \)であり,\( \ {\dot E}_{\mathrm {ab}} \ \)を基準フェーザとすれば,\( \ {\dot E}_{\mathrm {ab}}=E \ \),\( \ {\dot E}_{\mathrm {bc}}=E\mathrm {e}^{\mathrm {j}\frac {4}{3}\pi } \ \),\( \ {\dot E}_{\mathrm {ca}}=E\mathrm {e}^{\mathrm {j}\frac {2}{3}\pi } \ \)で表される。
一般に,\( \ n \ \)相の多相交流回路の消費電力は,\( \ \left( n-1 \right) \ \)個の単相電力計を用いて測定できる。これは\( \ \fbox { (1) } \ \)の定理と呼ばれる。\( \ \mathrm {W_{a}} \ \)及び\( \ \mathrm {W_{c}} \ \)は,この定理に基づいて三相交流回路の消費電力を求める単相電力計で,内部損失や誤差が無い理想的なものである。なお,\( \ \mathrm {W_{a}} \ \)は電流\( \ {\dot I}_{\mathrm {a}} \ \)が矢印の向きに流れたときに,\( \ \mathrm {W_{c}} \ \)は電流\( \ {\dot I}_{\mathrm {c}} \ \)が矢印の向きに流れたときに正を指示するように接続されている。
まず,\( \ {\dot I}_{\mathrm {a}} \ \)の実効値\( \ \left| {\dot I}_{\mathrm {a}}\right| \ \)を求めると\( \ \fbox { (2) } \ \mathrm {[A]} \ \)が得られる。また,\( \ \mathrm {W_{a}} \ \)の指示値は,\( \ {\dot E}_{\mathrm {ab}} \ \)に\( \ {\dot I}_{\mathrm {a}} \ \)の共役複素数を乗じた複素電力の実部を求めることで得られ,\( \ \fbox { (3) } \ \mathrm {[W]} \ \)となる。
同様に,\( \ {\dot I}_{\mathrm {c}} \ \)の実効値\( \ \left| {\dot I}_{\mathrm {c}}\right| \ \)及び\( \ \mathrm {W_{c}} \ \)の指示値は,それぞれ,\( \ \fbox { (4) } \ \mathrm {[A]} \ \)及び\( \ \fbox { (5) } \ \mathrm {[W]} \ \)となる。
以上から,図の三相交流回路で消費する電力は,\( \ \fbox { (1) } \ \)の定理より,\( \ \fbox { (3) } \ + \ \fbox { (5) } \ \mathrm {[W]} \ \)となる。
〔問5の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {\sqrt {7}E}{5R} &(ロ)& \frac {E^{2}}{2R} &(ハ)& \frac {\sqrt {7}E^{2}}{5R} \\[ 5pt ]
&(ニ)& -\frac {E^{2}}{2R} &(ホ)& プロンデル &(ヘ)& \frac {3E^{2}}{2R} \\[ 5pt ]
&(ト)& \frac {3E^{2}}{10R} &(チ)& \frac {\sqrt {7}E}{2R} &(リ)& \frac {\sqrt {3}E}{2R} \\[ 5pt ]
&(ヌ)& \frac {3E}{10R} &(ル)& \frac {\sqrt {3}E}{5R} &(ヲ)& \frac {\sqrt {3}E^{2}}{5R} \\[ 5pt ]
&(ワ)& ノートン &(カ)& \frac {E}{2R} &(ヨ)& テブナン \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
三相回路における不平衡負荷を接続したときの電流値と消費電力を求める問題で,計算量が多いので丁寧に解いていく必要がある問題です。
\( \ 1 \ \)種の理論科目においては不平衡の\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y}-\Delta \ \)変換は毎年のように出題される問題です。やや式は長いですが,必ず扱えるようにしておきましょう。
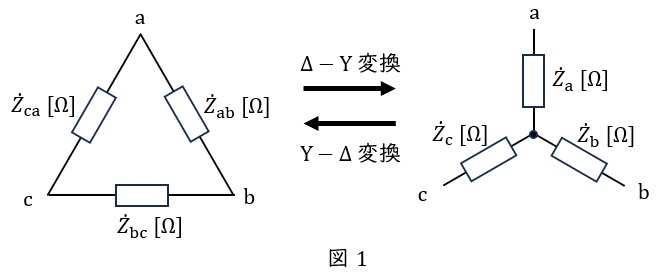
1.\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y}-\Delta \ \)変換
①\( \ \Delta -\mathrm {Y} \ \)変換
図1において,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {a}}&=&\frac {{\dot Z}_{\mathrm {ab}}{\dot Z}_{\mathrm {ca}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
{\dot Z}_{\mathrm {b}}&=&\frac {{\dot Z}_{\mathrm {bc}}{\dot Z}_{\mathrm {ab}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
{\dot Z}_{\mathrm {c}}&=&\frac {{\dot Z}_{\mathrm {ca}}{\dot Z}_{\mathrm {bc}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
\end{eqnarray}
\]
②\( \ \mathrm {Y}-\Delta \ \)変換
図1において,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {c}}} \\[ 5pt ]
{\dot Z}_{\mathrm {bc}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {a}}} \\[ 5pt ]
{\dot Z}_{\mathrm {ca}}&=&\frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {b}}} \\[ 5pt ]
\end{eqnarray}
\]
平衡三相回路においては,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}}={\dot Z}_{\mathrm {bc}}&=&{\dot Z}_{\mathrm {ca}}=3{\dot Z}_{\mathrm {a}}=3{\dot Z}_{\mathrm {b}}=3{\dot Z}_{\mathrm {c}} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.複素電力
送電端電圧を\( \ {\dot V}_{\mathrm {s}} \ \mathrm {[V]} \ \),受電端電圧を\( \ {\dot V}_{\mathrm {r}} \ \mathrm {[V]} \ \),送電線電流を\( \ \dot I \ \mathrm {[A]} \ \)とすると,受電端への送電電力\( \ P+\mathrm {j}Q \ \mathrm {[V\cdot A]} \ \)は遅れ無効電力を正とすると,
\[
\begin{eqnarray}
P+\mathrm {j}Q&=&{\dot V}_{\mathrm {r}}\overline {\dot I} \\[ 5pt ]
\end{eqnarray}
\]
で求められます。ただし,\( \ \overline {\dot I} \ \)は\( \ \dot I \ \)の共役複素数であり,\( \ \dot I =I_{\mathrm {r}}+\mathrm {j}I_{\mathrm {i}} \ \)であるとき,\( \ \overline {\dot I}=I_{\mathrm {r}}-\mathrm {j}I_{\mathrm {i}} \ \)となります。
【解答】
(1)解答:ホ
題意より解答候補は,(ホ)プロンデル,(ワ)ノートン,(ヨ)テブナン,になると思います。
一般に\( \ n \ \)相の多相交流回路の消費電力は,\( \ \left( n-1 \right) \ \)個の単相電力計を用いて測定できるという定理をプロンデルの定理といいます。電験では二電力計法しか出題されないため,二電力計法を知っておけば良いでしょう。
(2)解答:イ
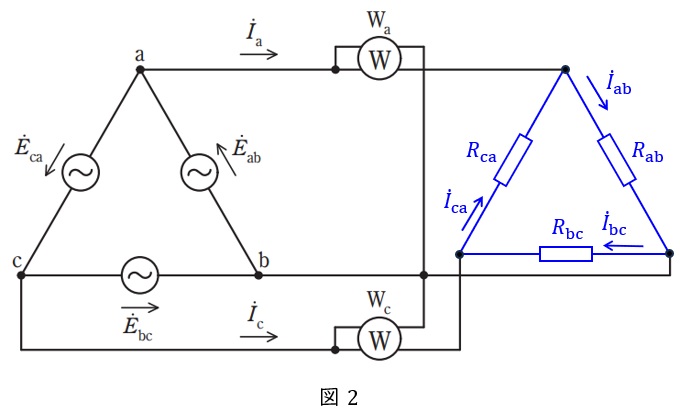
図2のように,不平衡負荷を\( \ \mathrm {Y}-\Delta \ \)変換したときの各電流を\( \ {\dot I}_{\mathrm {ab}} \ \),\( \ {\dot I}_{\mathrm {bc}} \ \),\( \ {\dot I}_{\mathrm {ca}} \ \),各抵抗を\( \ R_{\mathrm {ab}} \ \),\( \ R_{\mathrm {bc}} \ \),\( \ R_{\mathrm {ca}} \ \)とおくと,ワンポイント解説「1.\( \ \Delta -\mathrm {Y} \ \)変換と\( \ \mathrm {Y}-\Delta \ \)変換」の通り,
\[
\begin{eqnarray}
R_{\mathrm {ab}}&=&\frac {R\cdot R+R\cdot 2R +2R\cdot R}{2R} \\[ 5pt ]
&=&\frac {5}{2}R \\[ 5pt ]
R_{\mathrm {bc}}&=&\frac {R\cdot R+R\cdot 2R +2R\cdot R}{R} \\[ 5pt ]
&=&5R \\[ 5pt ]
R_{\mathrm {ca}}&=&\frac {R\cdot R+R\cdot 2R +2R\cdot R}{R} \\[ 5pt ]
&=&5R \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,\( \ {\dot I}_{\mathrm {ab}} \ \),\( \ {\dot I}_{\mathrm {bc}} \ \),\( \ {\dot I}_{\mathrm {ca}} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {ab}}&=&\frac {{\dot E}_{\mathrm {ab}}}{R_{\mathrm {ab}}} \\[ 5pt ]
&=&\frac {E}{\displaystyle \frac {5}{2}R} \\[ 5pt ]
&=&\frac {2E}{5R} \\[ 5pt ]
{\dot I}_{\mathrm {bc}}&=&\frac {{\dot E}_{\mathrm {bc}}}{R_{\mathrm {bc}}} \\[ 5pt ]
&=&\frac {E\mathrm {e}^{\mathrm {j}\frac {4}{3}\pi }}{5R} \\[ 5pt ]
&=&\frac {E}{5R}\mathrm {e}^{\mathrm {j}\frac {4}{3}\pi } \\[ 5pt ]
&=&\frac {E}{5R}\left( \cos \frac {4}{3}\pi +\mathrm {j}\sin \frac {4}{3}\pi \right) \\[ 5pt ]
&=&\frac {E}{5R}\left( -\frac {1}{2} -\mathrm {j}\frac {\sqrt {3}}{2} \right) \\[ 5pt ]
&=&-\frac {E}{10R}-\mathrm {j}\frac {\sqrt {3}E}{10R} \\[ 5pt ]
{\dot I}_{\mathrm {ca}}&=&\frac {{\dot E}_{\mathrm {ca}}}{R_{\mathrm {ca}}} \\[ 5pt ]
&=&\frac {E\mathrm {e}^{\mathrm {j}\frac {2}{3}\pi }}{5R} \\[ 5pt ]
&=&\frac {E}{5R}\mathrm {e}^{\mathrm {j}\frac {2}{3}\pi } \\[ 5pt ]
&=&\frac {E}{5R}\left( \cos \frac {2}{3}\pi +\mathrm {j}\sin \frac {2}{3}\pi \right) \\[ 5pt ]
&=&\frac {E}{5R}\left( -\frac {1}{2} +\mathrm {j}\frac {\sqrt {3}}{2} \right) \\[ 5pt ]
&=&-\frac {E}{10R}+\mathrm {j}\frac {\sqrt {3}E}{10R} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,\( \ {\dot I}_{\mathrm {a}} \ \)は,キルヒホッフの法則より,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}}&=&{\dot I}_{\mathrm {ab}}-{\dot I}_{\mathrm {ca}} \\[ 5pt ]
&=&\frac {2E}{5R}-\left( -\frac {E}{10R}+\mathrm {j}\frac {\sqrt {3}E}{10R}\right) \\[ 5pt ]
&=&\frac {E}{2R}-\mathrm {j}\frac {\sqrt {3}E}{10R} \\[ 5pt ]
\end{eqnarray}
\]
となるので,その実効値\( \ \left| {\dot I}_{\mathrm {a}}\right| \ \)は,
\[
\begin{eqnarray}
\left| {\dot I}_{\mathrm {a}}\right| &=&\sqrt {\left( \frac {E}{2R}\right) ^{2}+\left( \frac {\sqrt {3}E}{10R}\right) ^{2}} \\[ 5pt ]
&=&\sqrt {\frac {E^{2}}{4R^{2}}+\frac {3E^{2}}{100R^{2}}} \\[ 5pt ]
&=&\sqrt {\frac {7E^{2}}{25R^{2}}} \\[ 5pt ]
&=&\frac {\sqrt {7}E}{5R} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ロ
\( \ {\dot E}_{\mathrm {ab}} \ \)に\( \ {\dot I}_{\mathrm {a}} \ \)の共役複素数を乗じた複素電力\( \ P_{\mathrm {a}}+\mathrm {j}Q_{\mathrm {a}} \ \)は,ワンポイント解説「2.複素電力」の通り,
\[
\begin{eqnarray}
P_{\mathrm {a}}+\mathrm {j}Q_{\mathrm {a}} &=&{\dot E}_{\mathrm {ab}}\overline {\dot I}_{\mathrm {a}} \\[ 5pt ]
&=&E \left( \frac {E}{2R}+\mathrm {j}\frac {\sqrt {3}E}{10R}\right) \\[ 5pt ]
&=&\frac {E^{2}}{2R}+\mathrm {j}\frac {\sqrt {3}E^{2}}{10R} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \mathrm {W_{a}} \ \)の指示値は\( \ \displaystyle \frac {E^{2}}{2R} \ \mathrm {[W]} \ \)と求められる。
(4)解答:ル
(2)と同様に\( \ {\dot I}_{\mathrm {c}} \ \)は,キルヒホッフの法則より,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {c}}&=&{\dot I}_{\mathrm {ca}}-{\dot I}_{\mathrm {bc}} \\[ 5pt ]
&=&\left( -\frac {E}{10R}+\mathrm {j}\frac {\sqrt {3}E}{10R}\right)-\left( -\frac {E}{10R}-\mathrm {j}\frac {\sqrt {3}E}{10R} \right) \\[ 5pt ]
&=&\mathrm {j}\frac {\sqrt {3}E}{5R} \\[ 5pt ]
\end{eqnarray}
\]
となるので,その実効値\( \ \left| {\dot I}_{\mathrm {c}}\right| \ \)は,\( \ \displaystyle \left| {\dot I}_{\mathrm {c}}\right| =\frac {\sqrt {3}E}{5R} \ \mathrm {[A]} \ \)と求められる。
(5)解答:ト
\( \ {\dot E}_{\mathrm {cb}} \ \)に\( \ {\dot I}_{\mathrm {c}} \ \)の共役複素数を乗じた複素電力\( \ P_{\mathrm {c}}+\mathrm {j}Q_{\mathrm {c}} \ \)は,ワンポイント解説「2.複素電力」の通り,
\[
\begin{eqnarray}
P_{\mathrm {c}}+\mathrm {j}Q_{\mathrm {c}} &=&{\dot E}_{\mathrm {cb}}\overline {\dot I}_{\mathrm {c}} \\[ 5pt ]
&=&-{\dot E}_{\mathrm {bc}}\overline {\dot I}_{\mathrm {c}} \\[ 5pt ]
&=&-E \left( -\frac {1}{2} -\mathrm {j}\frac {\sqrt {3}}{2} \right) \left( -\mathrm {j}\frac {\sqrt {3}E}{5R}\right) \\[ 5pt ]
&=&\frac {3E^{2}}{10R}-\mathrm {j}\frac {\sqrt {3}E^{2}}{10R} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \mathrm {W_{c}} \ \)の指示値は\( \ \displaystyle \frac {3E^{2}}{10R} \ \mathrm {[W]} \ \)と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん