【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,電界効果トランジスタの原理に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
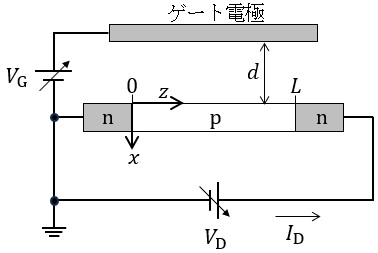
図のように,\( \ \mathrm {n} \ \)形半導体と\( \ \mathrm {p} \ \)形半導体を,左から\( \ \mathrm {n}-\mathrm {p}-\mathrm {n} \ \)の順に接合させた構造に対して,距離\( \ d \ \)を隔てて平行に金属ゲート電極を配置する。\( \ \mathrm {n}-\mathrm {p}-\mathrm {n} \ \)構造及びゲート電極の,紙面の奥行き方向の長さを\( \ W \ \)とする。\( \ \mathrm {p} \ \)形半導体の長さを\( \ L \ \)とし,電極及び\( \ \mathrm {n} \ \)形半導体中の抵抗は無視する。また,ゲート電極と半導体間の誘電率を\( \ \varepsilon \ \)とする。
図の回路において,\( \ V_{\mathrm {D}}=0 \ \)とし,\( \ V_{\mathrm {G}}>0 \ \)を印加した場合を考える。平行平板導体間の静電誘導によって,ゲート電極下面に正の面電荷密度\( \ +\sigma \ \)が,半導体側には負の面電荷密度\( \ -\sigma \ \)が誘起される。ただし,\( \ L≫d \ \),\( \ W≫d \ \)と仮定し,端部効果は無視する。ゲート電極と半導体の間の電界の\( \ x \ \)方向成分を\( \ E_{x} \ \)と定義すると,\( \ \sigma \ \)は\( \ E_{x} \ \)と\( \ \varepsilon \ \)を用いて次のように表される。
\[
\begin{eqnarray}
\sigma &=& \ \fbox { (1) } \ \ ・・・・・・・・・・・・・・・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
半導体側に誘起される負の電荷は電子の流入によって生じるが,\( \ \mathrm {p} \ \)形半導体には多数の正孔が存在するため,流入した電子は正孔との再結合で消滅する。表面における正孔の面電荷密度を\( \ \displaystyle \frac {\varepsilon }{d} V_{\mathrm {th}} \ \)と仮定すると,\( \ \mathrm {p} \ \)形半導体表面に誘起される電子の面電荷密度の大きさ\( \ \sigma _{\mathrm {e}} \ \)は,\( \ \sigma \ \)から正孔の面電荷密度を減じた大きさになる。すなわち,
\[
\begin{eqnarray}
\sigma _{\mathrm {e}} &=& \sigma -\frac {\varepsilon }{d} V_{\mathrm {th}} ・・・・・・・・・・・・・・・・・・・・・・・・ ② \\[ 5pt ]
\end{eqnarray}
\]
ただし,\( \ V_{\mathrm {th}} \ \)は,\( \ \mathrm {p} \ \)形半導体表面の正孔を打ち消すのに必要な\( \ V_{\mathrm {G}} \ \)に相当し,しきい値電圧と呼ばれる。
次に,\( \ V_{\mathrm {G}}>0 \ \),\( \ V_{\mathrm {D}}>0 \ \)の場合を考える。図に示す\( \ z \ \)座標を用いて\( \ \mathrm {p} \ \)形半導体表面の電位を\( \ V_{\mathrm {C}}\left( z\right) \ \)と定義する。位置\( \ z \ \)における\( \ E_{x} \ \)は,\( \ V_{\mathrm {C}}\left( z\right) \ \),\( \ V_{\mathrm {G}} \ \),\( \ d \ \)を用いて次のように表される。
\[
\begin{eqnarray}
E_{x} &=& \ \fbox { (2) } ・・・・・・・・・・・・・・・・・・・・・・・・ ③ \\[ 5pt ]
\end{eqnarray}
\]
②式に,①式,③式を代入すると,\( \ \sigma _{\mathrm {e}} \ \)は次のように表される。
\[
\begin{eqnarray}
\sigma _{\mathrm {e}} &=&\frac {\varepsilon }{d}\left( \ \fbox { (3) } \ \right) \ ・・・・・・・・・・・・・・・・・・・・・ ④ \\[ 5pt ]
\end{eqnarray}
\]
\( \ \mathrm {p} \ \)形半導体表面に電子が誘起されている状況では,\( \ \mathrm {p} \ \)形半導体表面が\( \ \mathrm {n} \ \)形に反転していることから,構造全体として\( \ \mathrm {n}-\mathrm {n}-\mathrm {n} \ \)接合となり,\( \ V_{\mathrm {D}}>0 \ \)の印加により,電流が流れる。面電荷密度\( \ -\sigma _{\mathrm {e}} \ \)の電子が電界により平均速度\( \ v \ \)でドリフト運動する場合の電流\( \ i_{\mathrm {D}} \ \)は,奥行き長さ\( \ W \ \)を考慮し,\( \ +z \ \)方向を正として次のように表される。
\[
\begin{eqnarray}
i _{\mathrm {D}} &=&-\sigma _{\mathrm {e}}Wv ・・・・・・・・・・・・・・・・・・・・・・・・・ ⑤ \\[ 5pt ]
\end{eqnarray}
\]
\( \ v \ \)は,電子の移動度\( \ \mu \ \)と,\( \ z \ \)方向の電界\( \ E_{z} \ \)を用いて次のように表される。ただし,\( \ \mu \ \)は場所によらず一定とする。
\[
\begin{eqnarray}
v &=&-\mu E_{z} \ \ ・・・・・・・・・・・・・・・・・・・・・・・・・・ ⑥ \\[ 5pt ]
\end{eqnarray}
\]
\( \ E_{z} \ \)は\( \ V_{\mathrm {C}}\left( z\right) \ \)を用いて次のように表される。
\[
\begin{eqnarray}
E_{z} &=&-\frac{ \partial V_{\mathrm {C}}\left( z\right) }{ \partial z } \ \ ・・・・・・・・・・・・・・・・・・・・・・・ ⑦ \\[ 5pt ]
\end{eqnarray}
\]
⑤式に,④式,⑥式,⑦式を代入し,\( \ I_{\mathrm {D}}=-i_{\mathrm {D}} \ \)の関係を用いると,\( \ I_{\mathrm {D}} \ \)は次のように表される。
\[
\begin{eqnarray}
I_{\mathrm {D}} &=&\frac {\varepsilon \mu W }{d}\left( \ \fbox { (3) } \ \right) \frac{ \partial V_{\mathrm {C}}\left( z\right) }{ \partial z } \ ・・・・・・・・・・・・・・・ ⑧ \\[ 5pt ]
\end{eqnarray}
\]
定常状態では,電流の連続性から,\( \ I_{\mathrm {D}} \ \)は位置\( \ z \ \)によらない定数となる。また,\( \ V_{\mathrm {th}} \ \)も\( \ z \ \)によらない定数であると仮定して,⑧式の両辺を\( \ z=0 \ \)から\( \ L \ \)まで\( \ z \ \)で積分すると,左辺の積分の値は\( \ \fbox { (4) } \ \)となる。右辺の積分も実行して,\( \ V_{\mathrm {C}}\left( 0\right) =0 \ \)及び\( \ V_{\mathrm {C}}\left( L\right) =V_{\mathrm {D}} \ \)を適用すると,\( \ I_{\mathrm {D}} \ \)は\( \ V_{\mathrm {D}} \ \)の関数として\( \ I_{\mathrm {D}}= \ \fbox { (5) } \ \)のように表される。
〔問6の解答群〕
\[
\begin{eqnarray}
&(イ)& I_{\mathrm {D}}L &(ロ)& \frac {d}{V_{\mathrm {G}}- V_{\mathrm {C}}\left( z\right) } &(ハ)& \varepsilon E_{x} \\[ 5pt ]
&(ニ)& V_{\mathrm {G}}-V_{\mathrm {th}}-V_{\mathrm {C}}\left( z\right) &(ホ)& \frac {I_{\mathrm {D}}}{L} &(ヘ)& \frac {\varepsilon E_{x}}{2} \\[ 5pt ]
&(ト)& 2\varepsilon E_{x} &(チ)& V_{\mathrm {G}}+V_{\mathrm {th}}-V_{\mathrm {C}}\left( z\right) &(リ)& \frac {V_{\mathrm {G}}- V_{\mathrm {C}}\left( z\right) }{d} \\[ 5pt ]
&(ヌ)& \frac {{I_{\mathrm {D}}}^{2}L}{2} &(ル)& \frac {V_{\mathrm {G}}+ V_{\mathrm {C}}\left( z\right) }{d} &(ヲ)& V_{\mathrm {G}}-V_{\mathrm {th}}+V_{\mathrm {C}}\left( z\right) \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
&(ワ)& \frac {\varepsilon \mu WL}{2d}\left[ 2\left( V_{\mathrm {G}}-V_{\mathrm {th}}\right) V_{\mathrm {D}}-{V_{\mathrm {D}}}^{2}\right] &(カ)& \frac {\varepsilon \mu W}{2dL}\left[ 2\left( V_{\mathrm {G}}-V_{\mathrm {th}}\right) V_{\mathrm {D}}-{V_{\mathrm {D}}}^{2}\right] \\[ 5pt ]
&(ヨ)& \frac {\varepsilon \mu W}{2dL}\left[ 2\left( V_{\mathrm {G}}-V_{\mathrm {th}}\right) V_{\mathrm {D}}+{V_{\mathrm {D}}}^{2}\right] && \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
電界効果トランジスタの原理を数式を用いて考える問題です。
\( \ 2 \ \)種まではあまり出題されなかったような内容で,電磁気の知識を応用したような内容です。
問題文が少し長いので読解が大変ですが,じっくり読んで正答できるようにしましょう。
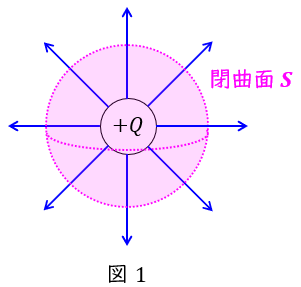
1.ガウスの法則
\( \ Q \ \mathrm {[C]} \ \)から出る電気力線は\( \ \displaystyle \frac {Q}{\varepsilon } \ \)本,電束は\( \ Q \ \)本であり,電界\( \ E \ \mathrm {[V / m]} \ \)及び電束密度\( \ D \ \mathrm {[C / m^{2}]} \ \)との関係は,任意の閉曲面において,
\[
\begin{eqnarray}
\int _{S} \boldsymbol E \cdot \mathrm {d}\boldsymbol S &=& \frac {Q}{\varepsilon } \\[ 5pt ]
\int _{S} \boldsymbol D \cdot \mathrm {d}\boldsymbol S &=& Q \\[ 5pt ]
\end{eqnarray}
\]
となり,これをガウスの法則といいます。
2.平行平板コンデンサの電界\( \ E \ \)と電圧\( \ V \ \)の関係
極板間の距離\( \ d \ \mathrm {[m]} \ \)の平行平板コンデンサに電圧\( \ V \ \mathrm {[V]} \ \)をかけると,極板間の電界\( \ E \ \mathrm {[V / m]} \ \)は,
\[
\begin{eqnarray}
E&=&\frac {V}{d} \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.平行平板コンデンサの電束密度\( \ D \ \)と電界\( \ E \ \)の関係
極板間の誘電率を\( \ \varepsilon \ \mathrm {[F / m]} \ \)とすると,電束密度\( \ D \ \mathrm {[C / m^{2}]} \ \)と電界\( \ E \ \mathrm {[V / m]} \ \)には,
\[
\begin{eqnarray}
D&=&\varepsilon E \\[ 5pt ]
\end{eqnarray}
\]
の関係があります。真空の誘電率を\( \ \varepsilon _{0} \ \mathrm {[F / m]} \ \),誘電体の比誘電率を\( \ \varepsilon _{\mathrm {r}} \ \)とすると,\( \ \varepsilon = \varepsilon _{\mathrm {r}}\varepsilon _{0} \ \)の関係があるので,
\[
\begin{eqnarray}
D&=&\varepsilon _{\mathrm {r}}\varepsilon _{0}E \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)解答:ハ
ワンポイント解説「1.ガウスの法則」より,面電荷密度\( \ \sigma \ \)から出る電束密度は\( \ \sigma \ \)となるので,\( \ \sigma \ \)と\( \ E_{x} \ \)の関係は,ワンポイント解説「3.平行平板コンデンサの電束密度\( \ D \ \)と電界\( \ E \ \)の関係」の通り,
\[
\begin{eqnarray}
\sigma &=&\varepsilon E_{x} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:リ
位置\( \ z \ \)におけるゲート電極下面と\( \ \mathrm {p} \ \)形半導体表面の電位差は\( \ V_{\mathrm {G}}- V_{\mathrm {C}}\left( z\right) \ \)なので,位置\( \ z \ \)における\( \ E_{x} \ \)は,ワンポイント解説「2.平行平板コンデンサの電界\( \ E \ \)と電圧\( \ V \ \)の関係」の通り,
\[
\begin{eqnarray}
E_{x} &=&\frac {V_{\mathrm {G}}- V_{\mathrm {C}}\left( z\right) }{d} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ニ
②式に,(1),(3)解答式を代入すると,\( \ \sigma _{\mathrm {e}} \ \)は,
\[
\begin{eqnarray}
\sigma _{\mathrm {e}} &=& \sigma -\frac {\varepsilon }{d} V_{\mathrm {th}} \\[ 5pt ]
&=& \varepsilon E_{x} -\frac {\varepsilon }{d} V_{\mathrm {th}} \\[ 5pt ]
&=& \varepsilon \frac {V_{\mathrm {G}}- V_{\mathrm {C}}\left( z\right) }{d} -\frac {\varepsilon }{d} V_{\mathrm {th}} \\[ 5pt ]
&=&\frac {\varepsilon }{d}\left\{ V_{\mathrm {G}}-V_{\mathrm {th}}-V_{\mathrm {C}}\left( z\right) \right\} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:イ
\( \ I_{\mathrm {D}} \ \)は位置\( \ z \ \)によらない定数であるので,⑧式の左辺の積分は,
\[
\begin{eqnarray}
\int _{0}^{L}I_{\mathrm {D}} \mathrm {d}z &=& \left[ I_{\mathrm {D}}z\right] _{0}^{L} \\[ 5pt ]
&=& I_{\mathrm {D}}L \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:カ
⑧式の右辺を積分すると,
\[
\begin{eqnarray}
\int _{0}^{L}\frac {\varepsilon \mu W }{d}\left\{ V_{\mathrm {G}}-V_{\mathrm {th}}-V_{\mathrm {C}}\left( z\right) \right\} \frac{ \partial V_{\mathrm {C}}\left( z\right) }{ \partial z } \mathrm {d}z &=&\frac {\varepsilon \mu W }{d}\int _{0}^{L}\left\{ V_{\mathrm {G}}-V_{\mathrm {th}}-V_{\mathrm {C}}\left( z\right) \right\} \frac{ \partial V_{\mathrm {C}}\left( z\right) }{ \partial z } \mathrm {d}z \\[ 5pt ]
&=&\frac {\varepsilon \mu W }{d}\int _{0}^{V_{\mathrm {D}}}\left\{ V_{\mathrm {G}}-V_{\mathrm {th}}-V_{\mathrm {C}}\left( z\right) \right\} \mathrm {d} V_{\mathrm {C}}\left( z\right) \\[ 5pt ]
&=&\frac {\varepsilon \mu W }{d}\left[ \left( V_{\mathrm {G}}-V_{\mathrm {th}}\right) V_{\mathrm {C}}\left( z\right) -\frac {V_{\mathrm {C}}\left( z\right) ^{2}}{2}\right] _{0}^{V_{\mathrm {D}}} \\[ 5pt ]
&=&\frac {\varepsilon \mu W }{d}\left\{ \left( V_{\mathrm {G}}-V_{\mathrm {th}}\right) V_{\mathrm {D}} -\frac {{V_{\mathrm {D}}} ^{2}}{2}\right\} \\[ 5pt ]
\end{eqnarray}
\]
となるので,これと(4)解答式より\( \ I_{\mathrm {D}} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {D}}L&=&\frac {\varepsilon \mu W }{d}\left\{ \left( V_{\mathrm {G}}-V_{\mathrm {th}}\right) V_{\mathrm {D}} -\frac {{V_{\mathrm {D}}} ^{2}}{2}\right\} \\[ 5pt ]
I_{\mathrm {D}}&=&\frac {\varepsilon \mu W }{dL}\left\{ \left( V_{\mathrm {G}}-V_{\mathrm {th}}\right) V_{\mathrm {D}} -\frac {{V_{\mathrm {D}}} ^{2}}{2}\right\} \\[ 5pt ]
&=&\frac {\varepsilon \mu W}{2dL}\left\{ 2\left( V_{\mathrm {G}}-V_{\mathrm {th}}\right) V_{\mathrm {D}}-{V_{\mathrm {D}}}^{2}\right\} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん