《機械・制御》〈誘導機〉[H21:問1]三相誘導電動機の電源側遮断器開放後の動作に関する計算・論説問題

【問題】

【難易度】★★☆☆☆（やや易しい）

三相誘導電動機の電源側遮断器を運転中に開放すると，誘導電動機の一次電圧はすぐに零とならず，いわゆる残留電圧が現れる。この残留電圧に関し，次の問に答えよ。

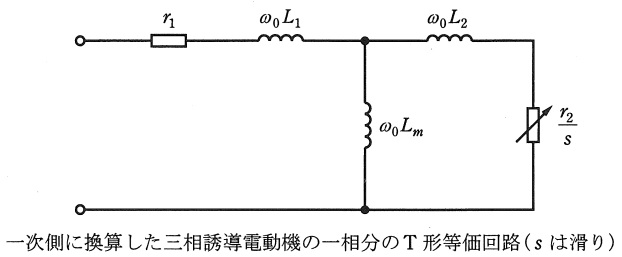
(1)　誘導電動機回転子に鎖交する磁束は二次電流に比例して減衰する。このときの開路時定数\( \ T_{o} \ \mathrm {[s]} \ \)を求めよ。ただし，誘導電動機は定格周波数が\( \ 60 \ \mathrm {[Hz]} \ \)，一次側に換算した\( \ \mathrm {T} \ \)形等価回路の定数は，一次抵抗\( \ r_{1} = 0.0198 \ \mathrm {[\Omega ]} \ \)，一次漏れリアクタンス\( \ \omega _{0}L_{1}= 0.501 \ \mathrm {[\Omega ]} \ \)，二次抵抗\( \ r_{2}=0.0198 \ \mathrm {[\Omega ]} \ \)，二次漏れリアクタンス\( \ \omega _{0}L_{2}= 0.501 \ \mathrm {[\Omega ]} \ \)及び励磁リアクタンス\( \ \omega _{0}L_{m}= 20.4 \ \mathrm {[\Omega ]} \ \)とする。ここでは，\( \ \omega _{0}= 2\pi \times 60=377 \ \mathrm {[rad/s]} \ \)として計算せよ。

(2)　ある相の残留電圧波形が遮断器開放時点からの時刻\( \ t \ \)を用いて近似的に次式で表されるものとする。
\[
\begin{eqnarray}
v_{a}&=&-\sqrt {2}\omega _{m}L_{m}I_{20}\mathrm {e}^{-\frac {t}{T_{o}}}\sin \left( \omega _{m}t+\theta _{0}\right) =-\sqrt {2}V_{a}\left( t\right) \sin \left( \omega _{m}t+\theta _{0}\right) \\[ 5pt ] \end{eqnarray}
\] ここで，\( \ \omega _{m} \ \)は\( \ 2 \ \)極機として考えたときの回転子角速度，\( \ I _{20} \ \)は遮断器開放直後の二次電流の実効値，\( \ \theta _{0} \ \)は遮断器開放直後の電圧位相角である。

時刻\( \ \displaystyle \frac {T_{o}}{2} \ \mathrm {[s]} \ \)において，回転子角速度\( \ \omega _{m} \ \)が遮断器開放直後の\( \ 80 \ \mathrm {[％]} \ \)となった。このときの残留電圧の大きさ\( \ V_{a}\left( t\right) \ \)は遮断器開放直後の電圧の何倍であるかを求めよ。ただし，自然対数の底\( \ \mathrm {e} \ \)の値は\( \ 2.718 \ \)とする。

(3)　力率改善用の進相コンデンサが誘導電動機端子に接続されている場合を考える。誘導電動機と進相コンデンサとが共通の遮断器で電源側から開放された場合の誘導電動機の残留電圧の様相について，この場合に進相コンデンサ容量が過大なときに生じる特有な異常現象名も挙げて説明せよ。

【ワンポイント解説】

三相誘導電動機の電源側遮断器開放後の動作に関する問題です。
(1)のイメージがピンとくるかどうかが勝負の分かれ目かと思います。
また，問題慣れをして，(2)のような読解問題を確実に得点できるように準備することが大事となります。

1.時定数
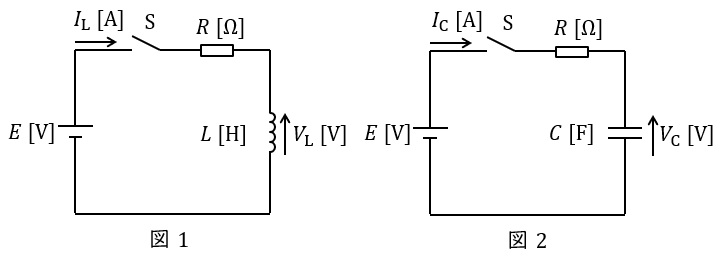
図1や図2のような回路が与えられるとき，図1のリアクトル電圧\( \ V_{\mathrm {L}} \ \mathrm {[V]} \ \)及び回路を流れる電流\( \ I_{\mathrm {L}} \ \mathrm {[A]} \ \)，図2のコンデンサ電圧\( \ V_{\mathrm {C}} \ \mathrm {[V]} \ \)及び回路を流れる電流\( \ I_{\mathrm {C}} \ \mathrm {[A]} \ \)はそれぞれ，
\[
\begin{eqnarray}
V_{\mathrm {L}} &=&E\mathrm {e}^{-\frac {R}{L}t} \\[ 5pt ] I_{\mathrm {L}} &=&\frac {E}{R}\left( 1-\mathrm {e}^{-\frac {R}{L}t}\right) \\[ 5pt ] V_{\mathrm {C}} &=&E\left( 1-\mathrm {e}^{-\frac {t}{CR}}\right) \\[ 5pt ] I_{\mathrm {C}} &=&\frac {E}{R}\mathrm {e}^{-\frac {t}{CR}} \\[ 5pt ] \end{eqnarray}
\] で求められ，上式の\( \ \mathrm {e} \ \)の指数が\( \ -1 \ \)（約\( \ 63.2 \ \mathrm {[％]} \ \)の変化）となる時間を時定数\( \ \tau \ \mathrm {[s]} \ \)と呼び\( \ \displaystyle \tau =\frac {L}{R} \ \)及び\( \ \tau =CR \ \)となります。

2.自己励磁現象
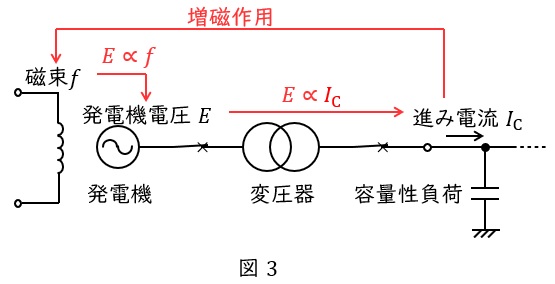
自己励磁現象は図3に示すように，同期発電機に負荷を接続する際に，系統が対地静電容量によって容量性負荷である時に電機子反作用が増磁作用に働くために発生する現象です。メカニズムは以下の通りです。
①　残留磁気の影響で発電機の誘導起電力が上昇する。
②　系統は容量性なので進み電流が流れる。
③　電機子反作用により増磁作用となる。
④　発電機の誘導起電力が上昇する。
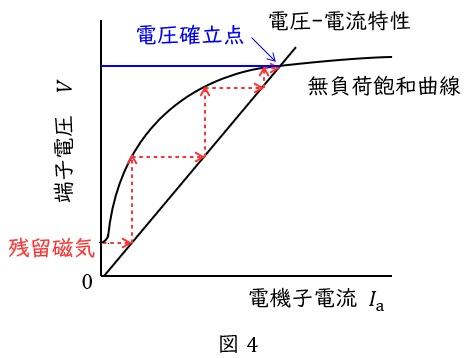
以後②～④を繰り返す。結果的に図4の無負荷飽和曲線との交点（電圧確立点）まで電圧が上昇する。

【解答】

(1)開路時定数\( \ T \ \mathrm {[s]} \ \)
電源側遮断器を開放した後は，二次電流は\( \ r_{2} \ \mathrm {[\Omega ]} \ \)，\( \ \omega _{0}L_{2} \ \mathrm {[\Omega ]} \ \)及び\( \ \omega _{0}L_{m} \ \mathrm {[\Omega ]} \ \)を流れその時定数\( \ T_{o} \ \mathrm {[s]} \ \)は，ワンポイント解説「1.時定数」の通り，
\[
\begin{eqnarray}
T_{o} &=&\frac {L_{2}+L_{m}}{r_{2}} \\[ 5pt ] \end{eqnarray}
\] となる。ここで，
\[
\begin{eqnarray}
L_{2} &=&\frac {0.501}{\omega _{0}} \\[ 5pt ] &=&\frac {0.501}{377} \\[ 5pt ] &≒&0.001 \ 328 \ 9 \ \mathrm {[H]} \\[ 5pt ] L_{m} &=&\frac {20.4}{\omega _{0}} \\[ 5pt ] &=&\frac {20.4}{377} \\[ 5pt ] &≒&0.054 \ 111 \ \mathrm {[H]} \\[ 5pt ] \end{eqnarray}
\] であるので，\( \ T_{o} \ \mathrm {[s]} \ \)の値は，
\[
\begin{eqnarray}
T_{o} &=&\frac {L_{2}+L_{m}}{r_{2}} \\[ 5pt ] &=&\frac {0.001 \ 328 \ 9+0.054 \ 111}{0.019 \ 8} \\[ 5pt ] &≒&2.800 \ 0　→　2.80 \ \mathrm {[s]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)時刻\( \ \displaystyle \frac {T_{o}}{2} \ \mathrm {[s]} \ \)において，残留電圧の大きさ\( \ V_{a}\left( t\right) \ \)は遮断器開放直後の電圧の何倍であるか
与えられている式より，
\[
\begin{eqnarray}
V_{a}\left( t \right) &=&\omega _{m}L_{m}I_{20}\mathrm {e}^{-\frac {t}{T_{o}}} \\[ 5pt ] \end{eqnarray}
\] であるから，遮断器開放直後の電圧\( \ V_{a}\left( 0 \right) \ \mathrm {[V]} \ \)は，
\[
\begin{eqnarray}
V_{a}\left( 0 \right) &=&\omega _{m}L_{m}I_{20}\mathrm {e}^{-\frac {0}{T_{o}}} \\[ 5pt ] &=&\omega _{m}L_{m}I_{20} \\[ 5pt ] \end{eqnarray}
\] となる。また，時刻\( \ \displaystyle \frac {T_{o}}{2} \ \mathrm {[s]} \ \)の電圧\( \ V_{a}\left( \displaystyle \frac {T_{o}}{2} \right) \ \mathrm {[V]} \ \)は，回転角速度が\( \ 80 \ \mathrm {[％]} \ \)になっていることから，
\[
\begin{eqnarray}
V_{a}\left( \frac {T_{o}}{2} \right) &=&0.8\omega _{m}L_{m}I_{20}\mathrm {e}^{\frac {-\frac {T_{o}}{2}}{T_{o}}} \\[ 5pt ] &=&0.8\omega _{m}L_{m}I_{20}\mathrm {e}^{-\frac {1}{2}} \\[ 5pt ] &=&\frac {0.8\omega _{m}L_{m}I_{20}}{\sqrt {\mathrm {e}}} \\[ 5pt ] \end{eqnarray}
\] となるので，その比は，
\[
\begin{eqnarray}
\frac {\displaystyle V_{a}\left( \frac {T_{o}}{2} \right) }{V_{a}\left( 0 \right) }&=&\frac {\displaystyle \frac {0.8\omega _{m}L_{m}I_{20}}{\sqrt {\mathrm {e}}}}{\omega _{m}L_{m}I_{20}} \\[ 5pt ] &=&\frac {0.8}{\sqrt {\mathrm {e}}} \\[ 5pt ] &=&\frac {0.8}{\sqrt {2.718}} \\[ 5pt ] &≒&0.48525　→　0.485 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)導電動機と進相コンデンサとが共通の遮断器で電源側から開放された場合の誘導電動機の残留電圧の様相について，この場合に進相コンデンサ容量が過大なときに生じる特有な異常現象名も挙げて説明
・進相コンデンサが接続されている状態なので，自己励磁現象に関する内容が記載されていれば加点されるかと思います。

(試験センター解答例)
進相コンデンサの静電容量を\( \ C \ \mathrm {[F]} \ \)，残留電圧の大きさと周波数をそれぞれ\( \ V \ \mathrm {[V]} \ \)と\( \ f \ \mathrm {[Hz]} \ \)とすると，
\[
\begin{eqnarray}
I_{C}&=&2\pi fCV \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] の大きさの進相電流が誘導電動機へ供給される。この進相電流は誘導電動機の回転子電流による磁束の増加を生じて電圧を上昇させるので，進相コンデンサがない場合よりも残留電圧は上昇傾向を示し，やがて減衰していく。

進相コンデンサ容量が大きすぎる場合には，異常に高い電圧になる場合があるので注意が必要である。これを自己励磁現象という。一般に，進相コンデンサ電流が誘導電動機の無負荷電流以下となるように進相コンデンサ容量を選定すれば，自己励磁現象の発生は防止できる。