Contents
【問題】
【難易度】★★★★☆(やや難しい)
図1のような\(2\)自由度制御系がある。ここで\( \ G(s) \ \)は制御対象,\( \ C(s) \ \)及び\( \ F(s) \ \)は補償器である。また,\( \ R(s) \ \)は目標値,\( \ D(s) \ \)は外乱,\( \ Y(s) \ \)は制御量,\( \ E(s) \ \)は制御偏差である。この制御系について,次の問に答えよ。
(1) 図1に示すフィードバック補償器\( \ C(s) \ \)の係数\( \ K_{\mathrm {P}} \ \)及び\( \ T_{\mathrm {I}} \ \)の名称を答えよ。
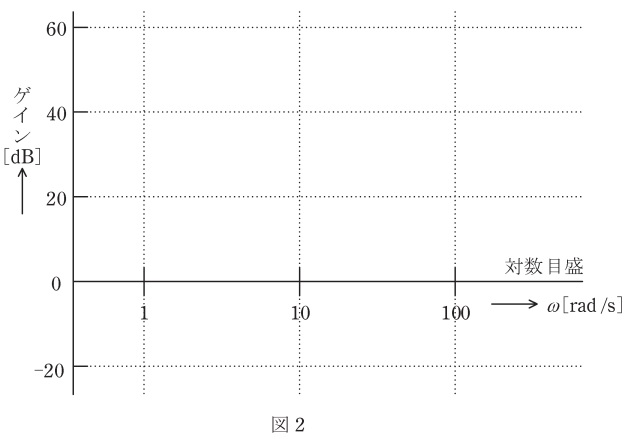
(2) \( \ K_{\mathrm {P}}=10 \ \),\( \ T_{\mathrm {I}}=0.1 \ \)のとき,\( \ C(s) \ \)の角周波数\( \ \omega \ \mathrm {[rad/s]} \ \)に対するゲイン特性の概形を答案用紙に印刷されている図2に折れ線近似で図示せよ。
(3) \( \ R(s)=0 \ \)として,外乱\( \ D(s) \ \)から制御偏差\( \ E(s) \ \)までの閉ループ伝達関数を求めよ。
(4) 上記小問(3)で求めた閉ループ伝達関数において,固有角周波数が\( \ 5 \ \mathrm {rad/s} \ \),減衰係数が\( \ 0.7 \ \)となるように,\( \ K_{\mathrm {P}} \ \)と\( \ T_{\mathrm {I}} \ \)の値を定めよ。
(5) \( \ D(s)=0 \ \)として,目標値\( \ R(s) \ \)から制御量\( \ Y(s) \ \)までの閉ループ伝達関数を\( \ F(s) \ \),\( \ C(s) \ \),\( \ G(s) \ \)を用いて求めよ。
(6) 上記小問(3)で求めた閉ループ伝達関数は\( \ F(s) \ \)に依存しない。また,上記小問(5)で求めた閉ループ伝達関数は\( \ C(s) \ \)に依存しない。これは制御系にどんな特長をもたらすか答えよ。この性質を利用しているのが\(2\)自由度制御系である。
【ワンポイント解説】
本問は(2)が最も難しい問題です。(2)がわからなくても(3)からは全く別の問題になることが分かれば,比較的高得点が望めるのではないかと思います。ただし,(1)や(6)のような問題は自動制御ではあまり出題されたことはなく,近年自動制御は新傾向が続いている気もします。
1.ゲイン\( \ g \ \)
周波数伝達関数\( \ G (\mathrm {j}\omega ) \ \)のゲイン\( \ g \ \)は,
\[
\begin{eqnarray}
g&=&20\log _{10}\left| G (\mathrm {j}\omega )\right| \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.減衰係数\( \ \zeta \ \)と固有振動数\( \ \omega _{\mathrm {n}} \ \)
2次遅れの伝達関数\( \ W(s) \ \)の一般式は,減衰係数\( \ \zeta \ \),固有振動数\( \ \omega _{\mathrm {n}} \ \)とすると,
\[
\begin{eqnarray}
W(s)&=&\frac {\omega _{\mathrm {n}}^{2}}{s^{2}+2\zeta \omega _{\mathrm {n}}s+\omega _{\mathrm {n}}^{2}} \\[ 5pt ]
\end{eqnarray}
\]
で表されます。
【解答】
(1)フィードバック補償器\( \ C(s) \ \)の係数\( \ K_{\mathrm {P}} \ \)及び\( \ T_{\mathrm {I}} \ \)の名称
\( \ K_{\mathrm {P}} \ \):比例ゲイン
\( \ T_{\mathrm {I}} \ \):積分時間
(2)\( \ C(s) \ \)の角周波数\( \ \omega \ \mathrm {[rad/s]} \ \)に対するゲイン特性の概形
\( \ C(s) \ \)に各値を代入すると,
\[
\begin{eqnarray}
C(s)&=&K_{\mathrm {P}}\left( 1+\frac {1}{T_{\mathrm {I}}s}\right) \\[ 5pt ]
&=&10\left( 1+\frac {1}{0.1s}\right) \\[ 5pt ]
&=&10\cdot \frac {0.1s+1}{0.1s} \\[ 5pt ]
\end{eqnarray}
\]
となるので,周波数伝達関数\( \ C(\mathrm {j}\omega ) \ \)は,
\[
\begin{eqnarray}
C(\mathrm {j}\omega )&=&10\cdot \frac {0.1\mathrm {j}\omega +1}{0.1\mathrm {j}\omega } \\[ 5pt ]
\end{eqnarray}
\]
となる。ワンポイント解説「1.ゲイン\( \ g \ \)」よりゲイン\( \ g \ \)は,
\[
\begin{eqnarray}
g&=&20\log _{10}\left| C (\mathrm {j}\omega )\right| \\[ 5pt ]
&=&20\log _{10}\left| 10\cdot \frac {0.1\mathrm {j}\omega +1}{0.1\mathrm {j}\omega } \right| \\[ 5pt ]
&=&20\log _{10}10+20\log _{10}\left| 0.1\mathrm {j}\omega +1\right| -20\log _{10}\left|0.1 \mathrm {j}\omega \right| \\[ 5pt ]
&=&20+20\log _{10}\sqrt {1+\left( 0.1\omega \right) ^{2} } -20\log _{10}0.1\omega \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,ゲイン\( \ g \ \)は,
\[
\begin{eqnarray}
g_{1}&=&20 \\[ 5pt ]
g_{2}&=&20\log _{10}\sqrt {1+\left( 0.1\omega \right) ^{2}} \\[ 5pt ]
g_{3}&=&-20\log _{10}0.1\omega \\[ 5pt ]
\end{eqnarray}
\]
の合成となる。\(g_{1}=20\)については一定の値となるので,図3-1のようになる。
\(g_{2}=20\log _{10}\sqrt {1+\left( 0.1\omega \right) ^{2}} \)については,\(\omega \)が小さい時(\(\omega <10\))は,
\[
\begin{eqnarray}
g_{2}&≒&20\log _{10}1 \\[ 5pt ]
&=&0 \\[ 5pt ]
\end{eqnarray}
\]
となり,\(\omega \)が大きい時(\(\omega >10\))は,
\[
\begin{eqnarray}
g_{2}&≒&20\log _{10} \sqrt {\left( 0.1\omega \right) ^{2} } \\[ 5pt ]
&=&20\log _{10}0.1 \omega \\[ 5pt ]
\end{eqnarray}
\]
となり,ゲインは図3-2に示すような形となる。
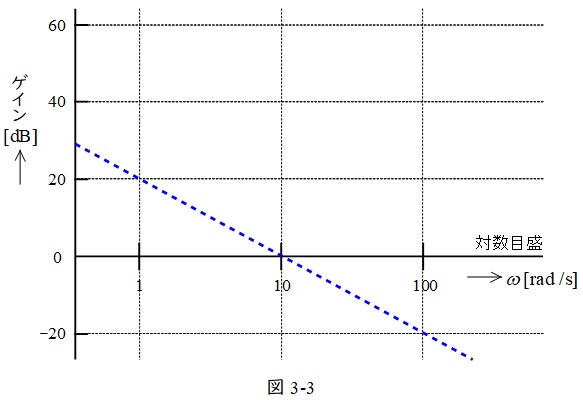
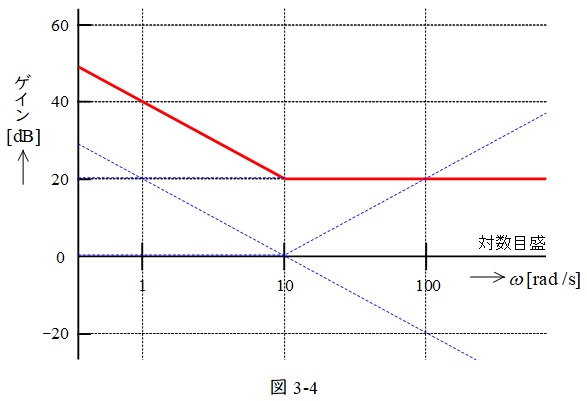
\(g_{3}=-20\log _{10}0.1\omega \)については,ゲインは図3-3に示すような形となる。したがって,図3-1~図3-3を合成すると,図3-4のように求められる。
(3)\( \ R(s)=0 \ \)として,外乱\( \ D(s) \ \)から制御偏差\( \ E(s) \ \)までの閉ループ伝達関数
図1より,各関数に関する関係式は,
\[
\begin{eqnarray}
\left[ D(s)+U(s)\right] G(s)&=&Y(s) &・・・・・・・①& \\[ 5pt ]
E(s)&=&-Y(s) &・・・・・・・②& \\[ 5pt ]
U(s)&=&E(s)C(s) &・・・・・・・③& \\[ 5pt ]
\end{eqnarray}
\]
であるから,③を①に代入すると,
\[
\begin{eqnarray}
\left[ D(s)+E(s)C(s)\right] G(s)&=&Y(s) \\[ 5pt ]
\end{eqnarray}
\]
となり,さらに②を代入すると,
\[
\begin{eqnarray}
D(s)G(s)+E(s)C(s)G(s)&=&-E(s) \\[ 5pt ]
D(s)G(s)&=&-\left( 1+C(s)G(s)\right) E(s) \\[ 5pt ]
\frac {E(s)}{D(s)}&=&-\frac {G(s)}{1+C(s)G(s)} \\[ 5pt ]
\end{eqnarray}
\]
となるので,各値を代入すると,
\[
\begin{eqnarray}
\frac {E(s)}{D(s)}&=&-\frac {\displaystyle \frac {1}{4s+1}}{\displaystyle 1+K_{\mathrm {P}}\left( 1+ \frac {1}{T_{\mathrm {I}}s}\right) \cdot \frac {1}{4s+1}} \\[ 5pt ]
&=&-\frac {1}{\displaystyle 4s+1+K_{\mathrm {P}}\left( 1+ \frac {1}{T_{\mathrm {I}}s}\right) } \\[ 5pt ]
&=&-\frac {T_{\mathrm {I}}s}{\displaystyle 4T_{\mathrm {I}}s^{2}+T_{\mathrm {I}}\left( 1+K_{\mathrm {P}}\right) s+K_{\mathrm {P}} } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)固有角周波数が\( \ 5 \ \mathrm {rad/s} \ \),減衰係数が\( \ 0.7 \ \)となるように,\( \ K_{\mathrm {P}} \ \)と\( \ T_{\mathrm {I}} \ \)の値
(3)の式を整理すると,
\[
\begin{eqnarray}
\frac {E(s)}{D(s)}&=&-\frac {\displaystyle \frac {s}{4}}{\displaystyle s^{2}+\frac {1+K_{\mathrm {P}} }{4} s+\frac {K_{\mathrm {P}}}{4T_{\mathrm {I}}} } \\[ 5pt ]
\end{eqnarray}
\]
となる。減衰係数\( \ \zeta \ \),固有振動数\( \ \omega _{\mathrm {n}} \ \)とすると,
\[
\begin{eqnarray}
2\zeta \omega _{\mathrm {n}}&=&\frac {1+K_{\mathrm {P}} }{4} \\[ 5pt ]
\omega _{\mathrm {n}}^{2}&=&\frac {K_{\mathrm {P}}}{4T_{\mathrm {I}}} \\[ 5pt ]
\end{eqnarray}
\]
となる。減衰係数\( \ \zeta \ \),固有振動数\( \ \omega _{\mathrm {n}} \ \)に値を代入すると,
\[
\begin{eqnarray}
\frac {1+K_{\mathrm {P}} }{4}&=&2\times 0.7\times 5 \\[ 5pt ]
1+K_{\mathrm {P}}&=&28 \\[ 5pt ]
K_{\mathrm {P}}&=&27 \\[ 5pt ]
\frac {K_{\mathrm {P}}}{4T_{\mathrm {I}}}&=&5^{2} \\[ 5pt ]
27&=&100T_{\mathrm {I}} \\[ 5pt ]
T_{\mathrm {I}}&=&0.27 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)\( \ D(s)=0 \ \)として,目標値\( \ R(s) \ \)から制御量\( \ Y(s) \ \)までの閉ループ伝達関数
図1より,\( \ D(s)=0 \ \)の時の各関数に関する関係式は,
\[
\begin{eqnarray}
R(s)\frac {F(s)}{G(s)}+E(s) C(s) &=&U(s) &・・・・・・・④& \\[ 5pt ]
R(s)F(s)-Y(s)&=&E(s) &・・・・・・・⑤& \\[ 5pt ]
U(s)G(s)&=&Y(s) &・・・・・・・⑥& \\[ 5pt ]
\end{eqnarray}
\]
となるので,⑤,⑥を④に代入すると,
\[
\begin{eqnarray}
R(s)\frac {F(s)}{G(s)}+\left[ R(s)F(s)-Y(s)\right] C(s) &=&\frac {Y(s)}{G(s)} \\[ 5pt ]
R(s)F(s)+\left[ R(s)F(s)-Y(s)\right] C(s)G(s) &=&Y(s) \\[ 5pt ]
R(s)F(s)+R(s)F(s)C(s)G(s)-Y(s)C(s)G(s) &=&Y(s) \\[ 5pt ]
R(s)F(s)+R(s)F(s)C(s)G(s) &=&Y(s)+Y(s)C(s)G(s) \\[ 5pt ]
R(s)F(s)\left\{ 1+C(s)G(s) \right\} &=&Y(s)\left\{ 1+C(s)G(s) \right\} \\[ 5pt ]
R(s)F(s)&=&Y(s) \\[ 5pt ]
\frac {Y(s)}{R(s)}&=&F(s) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(6)小問(3)で求めた閉ループ伝達関数は\( \ F(s) \ \)に依存せず,小問(5)で求めた閉ループ伝達関数は\( \ C(s) \ \)に依存しない。これは制御系にどんな特長をもたらすか
目標値応答特性は\(F(s)\)で指定し,外乱に対するフィードバック制御特性は\(C(s)\)で指定できるので,それぞれの特性を独立して指定できる。例えば,外乱に対する応答は早くし,目標値に対する応答はゆっくりにする等個別に制御することが可能となる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは