Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,抵抗回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる式又は数値を解答群の中から選び,その記号をマークシートに記入しなさい。
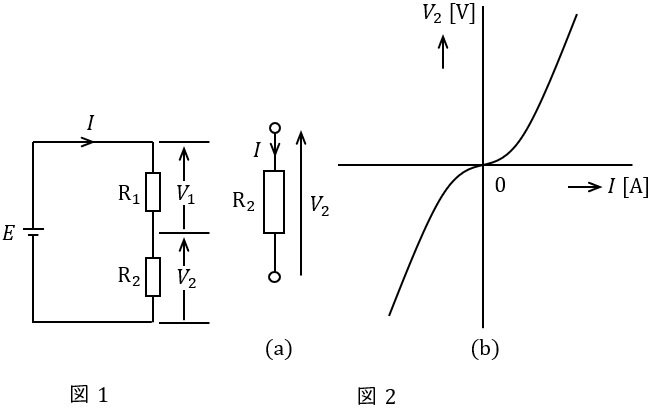
図1の回路は\( \ V_{1}=R_{1}I \ \)なる電圧・電流特性をもつ線形抵抗\( \ \mathrm {R_{1}} \ \)と\( \ V_{2}=\alpha I+\beta I\left| I\right| \ \)なる電圧・電流特性をもつ図2のような非線形抵抗\( \ \mathrm {R_{2}} \ \)の直列接続に直流電圧源\( \ E \ \)を接続した回路である。ただし,\( \ E=6 \ \mathrm {[V]} \ \),\( \ R_{1}=0.8 \ \mathrm {[\Omega ]} \ \),\( \ \alpha =2.2 \ \mathrm {[\Omega ]} \ \),\( \ \displaystyle \beta =\frac {2}{3} \ \mathrm {[V / A^{2}]} \ \)とする。
キルヒホッフの電圧則により図1の\( \ V_{1} \ \)と\( \ V_{2} \ \)の和は\( \ E \ \)に等しいという条件から回路方程式が得られる。ここにおいて,\( \ I > 0 \ \)とすれば,この方程式は\( \ \fbox { (1) } \ \)となる。\( \ R_{1} \ \),\( \ \alpha \ \),\( \ \beta \ \)及び\( \ E \ \)に与えられた数値を代入して\( \ I \ \)を求めると\( \ I= \ \fbox { (2) } \ \mathrm {[A]} \ \)となる。したがって,線形抵抗\( \ \mathrm {R_{1}} \ \)の両端の電圧は\( \ V_{1}= \ \fbox { (3) } \ \mathrm {[V]} \ \),非線形抵抗\( \ \mathrm {R_{2}} \ \)の両端の電圧は\( \ V_{2}= \ \fbox { (4) } \ \mathrm {[V]} \ \)となる。また,二つの抵抗で消費される電力の合計値は\( \ \fbox { (5) } \ \mathrm {[W]} \ \)となる。
また,\( \ I≦0 \ \)とすれば物理的に意味のある実数値としての電流\( \ I \ \)は得られないことがわかる。
〔問3の解答群〕
\[
\begin{eqnarray}
&(イ)& \left( R_{1}+\alpha \right) I=E &(ロ)& 6 &(ハ)& 4.8 \\[ 5pt ]
&(ニ)& \left( R_{1}+\alpha \right) I+\beta I^{2}=E &(ホ)& 36 &(ヘ)& 9 \\[ 5pt ]
&(ト)& 1.6 &(チ)& -10.8 &(リ)& 7.07 \\[ 5pt ]
&(ヌ)& 17.3 &(ル)& \left( R_{1}+\alpha \right) I-\beta I^{2}=E &(ヲ)& 1.2 \\[ 5pt ]
&(ワ)& 1.5 &(カ)& 2 &(ヨ)& 5 \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
非線形抵抗を含む直流回路の計算を行う問題です。
非線形抵抗自体の電験での出題は少ないので戸惑うかもしれませんが,しっかりと問題文を読んでいけば解ける問題です。
計算量もさほど多くないため,完答を目指すようにして下さい。
1.キルヒホッフの法則
キルヒホッフの法則には第1法則と第2法則がありますが,法則を説明できる必要はなく,計算で使いこなせることが重要です。
①第1法則(電流則)
回路の接続点に流入する電流の和と流出する電流の和が等しい。
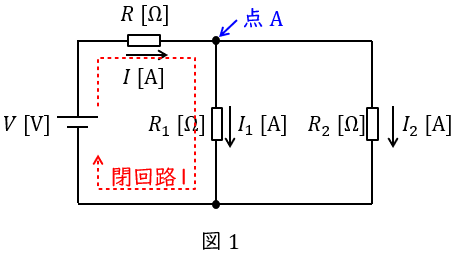
図1で言えば,例えば接続点\( \ \mathrm {A} \ \)において,
\[
\begin{eqnarray}
I &=&I_{1}+I_{2} \\[ 5pt ]
\end{eqnarray}
\]
となります。
②第2法則(電圧則)
任意の閉回路において,起電力の総和と抵抗の電圧降下の和は等しい。
図1で言えば,例えば閉回路\( \ 1 \ \)において,
\[
\begin{eqnarray}
V &=&RI+R_{1}I_{1} \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)解答:ニ
\( \ I > 0 \ \)のとき,
\[
\begin{eqnarray}
V_{2} &=&\alpha I+\beta I^{2} \\[ 5pt ]
\end{eqnarray}
\]
となるので,キルヒホッフの電圧則を適用し回路方程式を立てると,ワンポイント解説「1.キルヒホッフの法則」の通り,
\[
\begin{eqnarray}
V_{1}+V_{2} &=&E \\[ 5pt ]
R_{1} I+\alpha I+\beta I^{2} &=&E \\[ 5pt ]
\left( R_{1}+\alpha \right) I+\beta I^{2} &=&E \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ワ
(1)解答式に各値を代入すると,
\[
\begin{eqnarray}
\left( 0.8+2.2 \right) I+\frac {2}{3} I^{2} &=&6 \\[ 5pt ]
3 I+\frac {2}{3} I^{2} &=&6 \\[ 5pt ]
9 I+2 I^{2} &=&18 \\[ 5pt ]
2 I^{2}+9 I-18 &=&0 \\[ 5pt ]
\left( 2 I-3 \right) \left( I +6 \right) &=&0 \\[ 5pt ]
I&=&\frac {3}{2},-6 → 1.5 \ \mathrm {[A]} \left( ∵ I > 0 \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ヲ
\( \ I=1.5 \ \mathrm {[A]} \ \)より,\( \ \mathrm {R_{1}} \ \)の両端の電圧\( \ V_{1} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V_{1} &=&R_{1} I \\[ 5pt ]
&=&0.8\times 1.5 \\[ 5pt ]
&=&1.2 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ハ
キルヒホッフの電圧則より\( \ \mathrm {R_{2}} \ \)の両端の電圧\( \ V_{2} \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
V_{2} &=&E-V_{1} \\[ 5pt ]
&=&6-1.2 \\[ 5pt ]
&=&4.8 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ヘ
二つの抵抗で消費される電力の合計は,電源の供給する電力と等しいのでその大きさ\( \ P \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P &=&EI \\[ 5pt ]
&=&6\times 1.5 \\[ 5pt ]
&=&9 \ \mathrm {[W]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは