Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
三相回路において\( \ 2 \ \)台の変圧器(それぞれ変圧器\( \ \mathrm {a} \ \),変圧器\( \ \mathrm {b} \ \)とする。)を並行して運転するものとした場合,次の問に答えよ。
(1) 一次電圧を\( \ {\dot V}_{1} \ \),\( \ 2 \ \)台の変圧器の巻数比(一次側巻数/二次側巻数)をそれぞれ\( \ n_{a} \ \),\( \ n_{b} \ \),短絡インピーダンス(二次側換算値)をそれぞれ\( \ {\dot Z}_{a} \ \),\( \ {\dot Z}_{b} \ \),二次側合計負荷電流を\( \ {\dot I}_{L} \ \)とした場合,各変圧器の二次側を流れる電流\( \ {\dot I}_{a} \ \),\( \ {\dot I}_{b} \ \)の式を求めよ。ただし,短絡インピーダンスの抵抗分は無視できるものとする。
(2) 上記(1)で求めた結果に基づき,各変圧器が,その容量に比例した電流を分担するための条件と両変圧器に循環電流が流れないための条件をそれぞれ説明せよ。
【ワンポイント解説】
変圧器の並行運転に関する問題です。
どちらかというと機械科目に出題されやすい並行運転の問題ですが,本問のように電力科目や電力管理科目でも出題される可能性があります。
分担電流と循環電流を分けて考えることがポイントです。
1.変圧器の巻数比と変圧比,変流比の関係
変圧器の一次側の巻数\( \ N_{1} \ \),電圧\( \ V_{1} \ \mathrm {[V]} \ \),電流\( \ I_{1} \ \mathrm {[A]} \ \),二次側の巻数\( \ N_{2} \ \),電圧\( \ V_{2} \ \mathrm {[V]} \ \),電流\( \ I_{2} \ \mathrm {[A]} \ \)とすると,巻数比\( \ \displaystyle a=\frac {N_{1}}{N_{2}} \ \)は,
\[
\begin{eqnarray}
a&=&\frac {N_{1}}{N_{2}} =\frac {V_{1}}{V_{2}}=\frac {I_{2}}{I_{1}} \\[ 5pt ]
\end{eqnarray}
\]
となります。インピーダンスは電圧を電流で割ったものであるため,一次側換算のインピーダンス\( \ Z_{1} \ \mathrm {[\Omega ]} \ \),二次側換算のインピーダンス\( \ Z_{2} \ \mathrm {[\Omega ]} \ \)とすると,
\[
\begin{eqnarray}
\frac {Z_{1}}{Z_{2}} &=&\frac {\displaystyle \frac {V_{1}}{I_{1}}}{\displaystyle \frac {V_{2}}{I_{2}}} \\[ 5pt ]
&=&\frac {V_{1}}{I_{1}}\times \frac {I_{2}}{V_{2}} \\[ 5pt ]
&=&\frac {V_{1}}{V_{2}}\times \frac {I_{2}}{I_{1}} \\[ 5pt ]
&=&\left( \frac {N_{1}}{N_{2}} \right) ^{2} \\[ 5pt ]
&=&a^{2} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.変圧器の並行運転の条件
変圧器の並行運転の条件は以下の通りとなります。
①極性が一致している
極性が一致していないと誘導起電力の位相が\( \ 180° \ \)ずれるため,各変圧器間に大きな循環電流が流れ,変圧器が過熱し焼損してしまう可能性があります。
②変圧比(≒巻数比)が一致している
巻数比が一致していないと各変圧器間に循環電流が流れ,変圧器が過熱したり,負荷に十分な電力を供給できない可能性があります。
③角変位が一致している
三相変圧器では\( \ \Delta −\mathrm {Y} \ \)結線や\( \ \mathrm {Y}−\Delta \ \)結線で一次側及び二次側にて位相が\( \ 30° \ \)ずれるので,角変位が一致していないと大きな循環電流が流れることになります。
④百分率インピーダンスが等しい
百分率インピーダンスが等しくないと,各変圧器が定格容量に応じた負荷を分担することができなくなります。
⑤変圧器本体の抵抗とリアクタンスの比が等しい
変圧器の二次側に流れる電流に位相差が生じ,取り出せる電力は各変圧器の出力の和より小さくなり,出力に対する銅損の割合が大きくなって利用率が悪くなります。
【解答】
(1)各変圧器の二次側を流れる電流\( \ {\dot I}_{a} \ \),\( \ {\dot I}_{b} \ \)の式
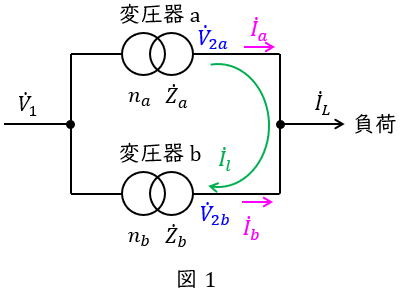
本問における変圧器の並行運転の状態を図に示すと図1のようになる。
変圧器\( \ \mathrm {a} \ \),\( \ \mathrm {b} \ \)の二次電圧\( \ {\dot V}_{2a} \ \)及び\( \ {\dot V}_{2b} \ \)は,巻数比がそれぞれ\( \ n_{a} \ \),\( \ n_{b} \ \)であることから,ワンポイント解説「1.変圧器の巻数比と変圧比,変流比の関係」の通り,
\[
\begin{eqnarray}
{\dot V}_{2a}&=&\frac {{\dot V}_{1}}{n_{a}} \\[ 5pt ]
{\dot V}_{2b}&=&\frac {{\dot V}_{1}}{n_{b}} \\[ 5pt ]
\end{eqnarray}
\]
となり,循環電流を\( \ {\dot I}_{l} \ \)とすると,
\[
\begin{eqnarray}
{\dot I}_{l}&=&\frac {\displaystyle {\dot V}_{2a}-{\dot V}_{2b}}{{\dot Z}_{a}+{\dot Z}_{b}} \\[ 5pt ]
&=&\frac {\displaystyle \frac {{\dot V}_{1}}{n_{a}}-\frac {{\dot V}_{1}}{n_{b}}}{{\dot Z}_{a}+{\dot Z}_{b}} \\[ 5pt ]
\end{eqnarray}
\]
となる。また,各変圧器の負荷電流\( \ {\dot I}_{L} \ \)の分担電流\( \ {\dot I}_{La} \ \)及び\( \ {\dot I}_{Lb} \ \)は,分流の法則より,
\[
\begin{eqnarray}
{\dot I}_{La}&=&\frac {{\dot Z}_{b}}{{\dot Z}_{a}+{\dot Z}_{b}}{\dot I}_{L} \\[ 5pt ]
{\dot I}_{Lb}&=&\frac {{\dot Z}_{a}}{{\dot Z}_{a}+{\dot Z}_{b}}{\dot I}_{L} \\[ 5pt ]
\end{eqnarray}
\]
となるので,各変圧器の二次側を流れる電流\( \ {\dot I}_{a} \ \),\( \ {\dot I}_{b} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{a}&=&{\dot I}_{La}+{\dot I}_{l} \\[ 5pt ]
&=&\frac {{\dot Z}_{b}}{{\dot Z}_{a}+{\dot Z}_{b}}{\dot I}_{L}+\frac {\displaystyle \frac {{\dot V}_{1}}{n_{a}}-\frac {{\dot V}_{1}}{n_{b}}}{{\dot Z}_{a}+{\dot Z}_{b}} \\[ 5pt ]
{\dot I}_{b}&=&{\dot I}_{Lb}-{\dot I}_{l} \\[ 5pt ]
&=&\frac {{\dot Z}_{a}}{{\dot Z}_{a}+{\dot Z}_{b}}{\dot I}_{L}-\frac {\displaystyle \frac {{\dot V}_{1}}{n_{a}}-\frac {{\dot V}_{1}}{n_{b}}}{{\dot Z}_{a}+{\dot Z}_{b}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)各変圧器が,その容量に比例した電流を分担するための条件と両変圧器に循環電流が流れないための条件
(ポイント)
・容量に比例した電流を分担するための条件は,負荷電流\( \ {\dot I}_{L} \ \)の分担電流\( \ {\dot I}_{La} \ \)及び\( \ {\dot I}_{Lb} \ \)から考えていきます。
・循環電流が流れないための条件は,ワンポイント解説「2.変圧器の並行運転の条件」の知識と循環電流\( \ {\dot I}_{l} \ \)の式を組み合わせて考えていきます。
(試験センター解答例)
(1)解答の右辺第1項は各変圧器によって分担される負荷電流,右辺第2項は両変圧器間を流れる循環電流を表す。
題意より,各変圧器で分担される負荷電流\( \ \left| {\dot I}_{aL}\right| \ \),\( \ \left| {\dot I}_{bL}\right| \ \)とすると
\[
\begin{eqnarray}
\left| {\dot I}_{aL}\right| : \left| {\dot I}_{bL}\right| &=& \left| \frac {{\dot Z}_{b}}{{\dot Z}_{a}+{\dot Z}_{b}}{\dot I}_{L}\right| : \left| \frac {{\dot Z}_{a}}{{\dot Z}_{a}+{\dot Z}_{b}}{\dot I}_{L}\right| = \left| {\dot Z}_{b}\right| : \left| {\dot Z}_{a}\right|= \left| \frac {1}{{\dot Z}_{a}}\right| : \left| \frac {1}{{\dot Z}_{b}}\right| \\[ 5pt ]
\end{eqnarray}
\]
となることから,各変圧器の容量に比例した電流を負担するためには,短絡インピーダンスが容量に逆比例することが条件であり,また,循環電流が流れないためには右辺第2項より\( \ n_{a}=n_{b} \ \),すなわち巻数比が等しいことが条件である。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは