《機械・制御》〈パワーエレクトロニクス〉[R07:問3]単相ダイオードブリッジ整流回路に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

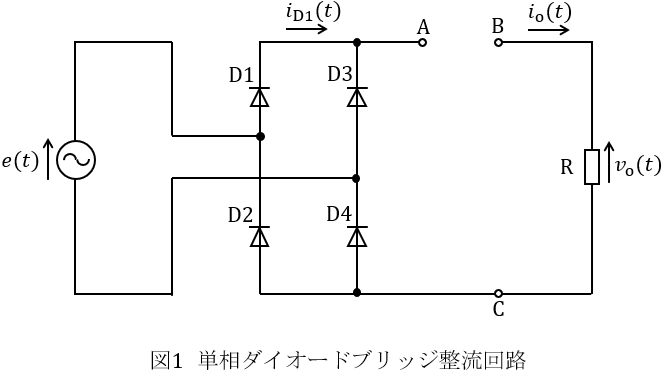
図1に単相ダイオードブリッジ整流回路を示す。電源は，実効値\( \ 100 \ \mathrm {V} \ \)，周波数\( \ 50 \ \mathrm {Hz} \ \)の単相交流電圧源である。負荷抵抗\( \ \mathrm {R}=10 \ \Omega \ \)として，次の問に答えよ。ただし，すべての回路素子は理想的で，回路は周期定常状態にあるものとする。

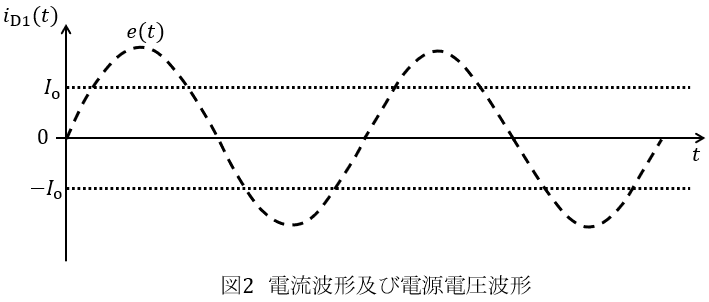
(1)　図1に示す回路の端子\( \ \mathrm {A} \ \)と端子\( \ \mathrm {B} \ \)の間にリアクトル\( \ \mathrm {L} \ \)を接続した場合を考える。このリアクトル\( \ \mathrm {L} \ \)のインダクタンスは十分に大きく，リアクトル\( \ \mathrm {L} \ \)を流れる電流\( \ i_{\mathrm {o}}\left( t \right) = I_{\mathrm {o}} \ \)は一定とする。答案用紙に図2と同じ図が描かれているので，ダイオード\( \ \mathrm {D1} \ \)に流れる電流\( \ i_{\mathrm {D1}}\left( t \right) \ \)を図示せよ。答案用紙には太い線で明確に描け。なお，同図には電源電圧\( \ e\left( t \right) \ \)が破線で，\( \ I_{\mathrm {o}} \ \)と\( \ -I_{\mathrm {o}} \ \)が点線で示してある。

(2)　小問(1)において，リアクトル\( \ \mathrm {L} \ \)の両端電圧の平均値\( \ V_{\mathrm {L}} \ \)を求めよ。

(3)　小問(2)の結果を考慮して，負荷抵抗\( \ \mathrm {R} \ \)の両端電圧\( \ v_{\mathrm {o}}\left( t \right) \ \)の平均値\( \ V_{\mathrm {o}} \ \)を求めよ。

(4)　図1に示す回路の端子\( \ \mathrm {A} \ \)と端子\( \ \mathrm {B} \ \)を短絡し，端子\( \ \mathrm {B} \ \)と端子\( \ \mathrm {C} \ \)の間にコンデンサ\( \ \mathrm {C} \ \)を接続した場合を考える。このとき，コンデンサに流れる電流の平均値\( \ I_{\mathrm {c}} \ \)を求めよ。

(5)　小問(4)のコンデンサの静電容量は十分に大きく，両端電圧の変動は無視できるとして，負荷抵抗\( \ \mathrm {R} \ \)に流れる電流\( \ i_{\mathrm {o}}\left( t \right) \ \)の平均値\( \ I_{\mathrm {o}} \ \)を求めよ。

(6)　小問(5)の負荷抵抗\( \ \mathrm {R} \ \)の平均消費電力\( \ P_{\mathrm {OC}} \ \)は，小問(1)で用いた回路での負荷抵抗\( \ \mathrm {R} \ \)の平均消費電力\( \ P_{\mathrm {OL}} \ \)の何倍か。

【ワンポイント解説】

単相ダイオードブリッジ整流回路に関する計算問題です。
動作原理とコンデンサとリアクトルの特性を理解している場合には，計算量も多くないため積極的に選択したい問題です。
これまで難易度が高いとして受験生から敬遠されてきたパワーエレクトロニクスですが，近年は比較的取り組みやすい問題が増えてきています。

1.単相ダイオードブリッジ整流回路の動作
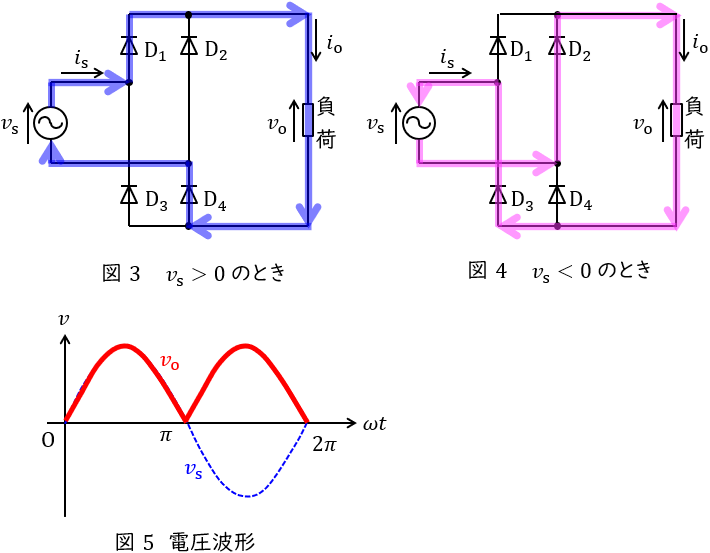
図3，図4に示す単相ダイオードブリッジ整流回路は以下のように動作します。

①\( \ v_{\mathrm {s}}＞0 \ \)のとき
図3のように，電流は交流電源→\( \ \mathrm {D}_{1} \ \)→負荷→\( \ \mathrm {D}_{4} \ \)→交流電源と流れます。出力電圧\( \ v_{\mathrm {o}} \ \)は素子の電圧降下が無視できるとすると，入力電圧\( \ v_{\mathrm {s}} \ \)と等しくなります。

②\( \ v_{\mathrm {s}}＜0 \ \)のとき
図4のように，電流は交流電源→\( \ \mathrm {D}_{2} \ \)→負荷→\( \ \mathrm {D}_{3} \ \)→交流電源と流れます。出力電圧\( \ v_{\mathrm {o}} \ \)は素子の電圧降下が無視できるとすると，\( \ -v_{\mathrm {s}} \ \)となります。

したがって，出力電圧の波形は図5のようになります。
図5より平均出力電圧\( \ V_{\mathrm {o}} \ \mathrm {[V]} \ \)は，交流入力\( \ v=\sqrt {2}V \sin \omega t \ \mathrm {[V]} \ \)とすると，
\[
\begin{eqnarray}
V_{\mathrm {o}} &=& \frac {1}{\pi }\int _{0}^{\pi }\sqrt {2}V\sin \omega t \mathrm {d}\omega t \\[ 5pt ] &=& \frac {\sqrt {2}}{\pi }V\left[ -\cos \omega t\right] _{0}^{\pi } \\[ 5pt ] &=& \frac {\sqrt {2}}{\pi }V\left( -\cos \pi +\cos 0 \right) \\[ 5pt ] &=& \frac {\sqrt {2}}{\pi }V\left\{ -\left( -1 \right) +1 \right\} \\[ 5pt ] &=& \frac {2\sqrt {2}}{\pi }V \\[ 5pt ] &≃& 0.90V \\[ 5pt ] \end{eqnarray}
\] となります。

2.コンデンサとリアクトルの平滑作用
整流回路の出力電圧や電流は波形の脈動が多いため，コンデンサやリアクトルを挿入し平滑させることがあります。

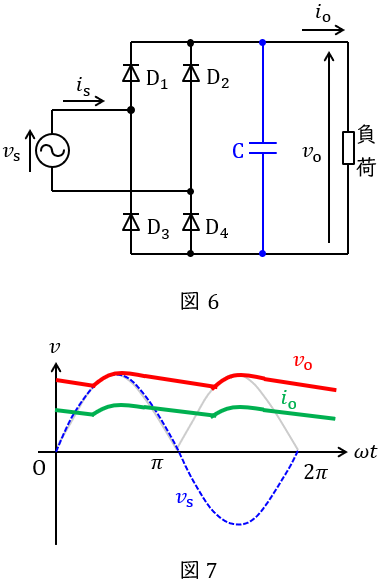
①コンデンサ
図6の示すように，負荷に並列にコンデンサを挿入することで，コンデンサの充放電により電圧波形の脈動が平滑されます。これにより，図7に示すような波形の出力が得られることになります。

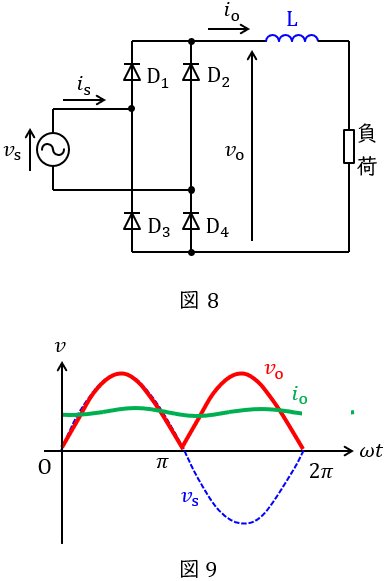
②リアクトル
図8に示すように，負荷に直列にリアクトルを挿入することで，リアクトルの作用により電流波形の脈動が平滑されます。これにより，図9に示すような波形の出力が得られることになります。

【解答】

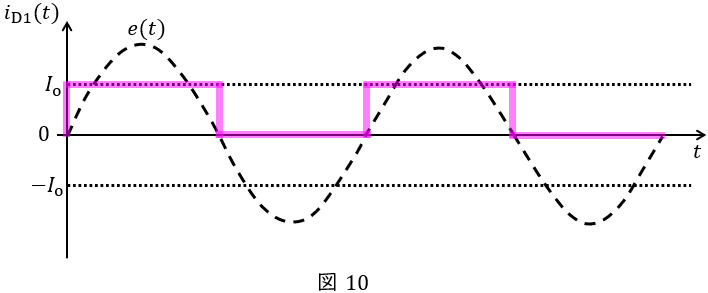
(1)ダイオード\( \ \mathrm {D1} \ \)に流れる電流\( \ i_{\mathrm {D1}}\left( t \right) \ \)を図示
ワンポイント解説「2.コンデンサとリアクトルの平滑作用」の通り，インダクタンスが十分に大きいリアクトル\( \ \mathrm {L} \ \)を接続した場合，出力電流\( \ i_{\mathrm {o}}\left( t \right) = I_{\mathrm {o}} \ \)で一定となる。また，ワンポイント解説「1.単相ダイオードブリッジ整流回路の動作」の通り，ダイオード\( \ \mathrm {D1} \ \)には\( \ e(t)\gt 0 \ \)のとき電流が流れるので，\( \ i_{\mathrm {D1}}\left( t \right) \ \)の波形は図10に示すような波形となる。

(2)リアクトル\( \ \mathrm {L} \ \)の両端電圧の平均値\( \ V_{\mathrm {L}} \ \)
リアクトル\( \ \mathrm {L} \ \)ではエネルギーの授受が行われるが，定常的には蓄えるエネルギーと放出するエネルギーが等しいので平均値は\( \ V_{\mathrm {L}}=0 \ \mathrm {[V]} \ \)となる。

(3)負荷抵抗\( \ \mathrm {R} \ \)の両端電圧\( \ v_{\mathrm {o}}\left( t \right) \ \)の平均値\( \ V_{\mathrm {o}} \ \)
平均出力電圧\( \ V_{\mathrm {o}} \ \mathrm {[V]} \ \)は，交流入力\( \ e\left( t \right) =100 \sqrt {2} \sin \omega t \ \mathrm {[V]} \ \)とすると，ワンポイント解説「1.単相ダイオードブリッジ整流回路の動作」の通り，
\[
\begin{eqnarray}
V_{\mathrm {o}} &=& \frac {1}{\pi }\int _{0}^{\pi }100 \sqrt {2}\sin \omega t \mathrm {d}\omega t \\[ 5pt ] &=& \frac {100 \sqrt {2}}{\pi }\left[ -\cos \omega t\right] _{0}^{\pi } \\[ 5pt ] &=& \frac {100 \sqrt {2}}{\pi }\left( -\cos \pi +\cos 0 \right) \\[ 5pt ] &=& \frac {100 \sqrt {2}}{\pi }\left\{ -\left( -1 \right) +1 \right\} \\[ 5pt ] &=& \frac {200\sqrt {2}}{\pi } \\[ 5pt ] &≃& 90.031　→　90.0 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)コンデンサに流れる電流の平均値\( \ I_{\mathrm {c}} \ \)
コンデンサにおいては，電荷の充放電を繰り返すが定常的には蓄えられる電荷量と放出される電荷量は等しい。したがって，電流の平均値は\( \ I_{\mathrm {c}}=0 \ \mathrm {[A]} \ \)となる。

(5)負荷抵抗\( \ \mathrm {R} \ \)に流れる電流\( \ i_{\mathrm {o}}\left( t \right) \ \)の平均値\( \ I_{\mathrm {o}} \ \)
静電容量の十分に大きいコンデンサを接続したとき，出力電圧\( \ v_{\mathrm {o}}\left( t \right) \ \)の平均値\( \ V_{\mathrm {o}} \ \mathrm {[V]} \ \)は，ワンポイント解説「2.コンデンサとリアクトルの平滑作用」の通り，
\[
\begin{eqnarray}
V_{\mathrm {o}} &=& 100\sqrt {2} \\[ 5pt ] &≒& 141.42 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となるので，負荷抵抗\( \ \mathrm {R}=10 \ [\Omega ] \ \)に流れる電流\( \ i_{\mathrm {o}}\left( t \right) \ \)の平均値\( \ I_{\mathrm {o}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {o}} &=& \frac {V_{\mathrm {o}}}{\mathrm {R}} \\[ 5pt ] &=& \frac {141.42}{10} \\[ 5pt ] &=& 14.142　→　14.1 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(6)平均消費電力\( \ P_{\mathrm {OC}} \ \)は\( \ P_{\mathrm {OL}} \ \)の何倍か
(3)解答より，リアクトル\( \ \mathrm {L} \ \)を接続したときの電流\( \ i_{\mathrm {o}}\left( t \right) \ \)の平均値\( \ I_{\mathrm {oL}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {oL}} &=& \frac {V_{\mathrm {oL}}}{\mathrm {R}} \\[ 5pt ] &=& \frac {90.031}{10} \\[ 5pt ] &=& 9.003 \ 1 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるので，平均消費電力\( \ P_{\mathrm {OC}} \ \)と\( \ P_{\mathrm {OL}} \ \)の比は，
\[
\begin{eqnarray}
\frac {P_{\mathrm {OC}}}{P_{\mathrm {OL}}} &=& \frac {\mathrm {R}{I_{\mathrm {oC}}}^{2}}{\mathrm {R}{I_{\mathrm {oL}}}^{2}} \\[ 5pt ] &=& \frac {{I_{\mathrm {oC}}}^{2}}{{I_{\mathrm {oL}}}^{2}} \\[ 5pt ] &=& \frac {14.142^{2}}{9.003 \ 1^{2}} \\[ 5pt ] &≒& 2.47 \\[ 5pt ] \end{eqnarray}
\] と求められる。