《機械・制御》〈自動制御〉[H27:問4]フィードバック制御系に関する計算問題

【問題】

【難易度】★☆☆☆☆（易しい）

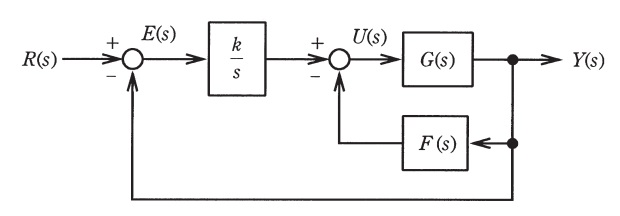
図に示すフィードバック制御系において，\(R(s)\)，\(E(s)\)，\(U(s)\)，\(Y(s)\)はそれぞれ，目標値\(r(t)\)，制御偏差\(e(t)\)，操作入力\(u(t)\)，制御量\(y(t)\)のラプラス変換を表している。また，\(G(s)\)は制御対象の伝達関数，\(\displaystyle \frac {k}{s}\)は積分動作の直列補償要素，\(F(s)\)はフィードバック補償要素を表している。

以下において，\(\displaystyle \frac {k}{s}\)と\(F(s)\)とに含まれる制御定数を調整することで，フィードバック制御系の目標値\(R(s)\)から制御量\(Y(s)\)までの伝達関数を，望ましい動特性を実現する参照モデルの伝達関数に一致させることを考える。次の問に答えよ。

(1)　制御対象は零点をもたない遅れ系であって，多項式\(h(s)\)を用いて次のように表されている。
\[
G(s)=\frac {1}{h(s)}
\] フィードバック制御系の目標値\(R(s)\)から制御量\(Y(s)\)までの伝達関数\(W(s)\)を\(s\)，\(k\)，\(F(s)\)，\(h(s)\)を用いて表せ。

(2)　制御対象は2次遅れ系
\[
G(s)=\frac {1}{h(s)}=\frac {1}{h_{0}+h_{1}s+h_{2}s^{2}}
\] であるとする。また，フィードバック補償要素\(f(s)\)は定数であるとし，
\[
F(s)=f_{0}
\] とおく。

次の参照モデルを導入する。
\[
W_{\mathrm {d}}(s)=\frac {1}{1+\sigma s+\alpha _{2}\sigma ^{2}s^{2}+\alpha _{3}\sigma ^{3}s^{3}}
\] ここで，\(\alpha _{2}\)及び\(\alpha _{3}\)は時間応答の形を規定する係数であり，\(\sigma \)は，その次数を\(s\)の次数と合わせているので，時間スケールのパラメータである。しかも，1次のモーメントに一致するので，立ち上がりの一つの特性値でもある。この\(\sigma \)も設計時の計算において決定する。

フィードバック制御系の目標値から制御量までの伝達関数\(W(s)\)と参照モデル\(W_{\mathrm {d}}(s)\)を一致させるために，パラメータ\(\sigma \)と制御定数\(k\)，\(f_{0}\)が満たさなくてはならない連立方程式を求めよ。

(3)　連立方程式を解いてパラメータ\(\sigma \)を\(\alpha _{2}\)，\(\alpha _{3}\)，\(h_{1}\)，\(h_{2}\)を用いて表せ。

(4)　制御定数\(k\)を求める式を\(\alpha _{2}\)，\(h_{1}\)，\(\sigma \)を用いて表せ。

(5)　制御定数\(f_{0}\)を求める式を\(k\)，\(h_{0}\)，\(\sigma \)を用いて表せ。

【ワンポイント解説】

近年の制御の問題の中でも非常に易しい問題です。伝達関数を正確に求めることができれば，後はそれほど難しい数式を使用しません。平成２７年の機械制御は問題毎の難易度差が大きいため，問1と本問を選択した方が大きく合格に近づいたのではないかと思います。

【解答】

(1)目標値\(R(s)\)から制御量\(Y(s)\)までの伝達関数\(W(s)\)
問題図より，伝達関数に関する連立方程式を立てると，
\[
\begin{eqnarray}
R(s)-Y(s) &=&E(s) &　・・・・・　①& \\[ 5pt ] E(s)\cdot \frac {k}{s}-Y(s)F(s)&=&U(s) &　・・・・・　②& \\[ 5pt ] U(s)G(s)&=& Y(s) ⇔ U(s)=h(s)Y(s) &　・・・・・　③&\\[ 5pt ] \end{eqnarray}
\] となるので，①，③を②に代入すると，
\[
\begin{eqnarray}
\left[ R(s)-Y(s)\right] \frac {k}{s}-Y(s)F(s)&=&h(s)Y(s) \\[ 5pt ] \frac {k}{s}R(s)-\frac {k}{s}Y(s) -Y(s)F(s)&=&h(s)Y(s) \\[ 5pt ] \frac {k}{s}R(s)&=&\frac {k}{s}Y(s) +Y(s)F(s)+h(s)Y(s) \\[ 5pt ] \frac {k}{s}R(s)&=&\left( \frac {k}{s} +F(s)+h(s)\right) Y(s) \\[ 5pt ] \frac {Y(s)}{R(s)}&=&\frac {\displaystyle \frac {k}{s}}{\displaystyle \frac {k}{s} +F(s)+h(s)} \\[ 5pt ] W(s)&=&\frac {1}{\displaystyle 1 +\frac {s}{k}\left[ F(s)+h(s)\right] } \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)パラメータ\(\sigma \)と制御定数\(k\)，\(f_{0}\)が満たさなくてはならない連立方程式
(1)の解答式に\(h(s)=h_{0}+h_{1}s+h_{2}s^{2}\)，\(F(s)=f_{0}\)を代入すると，
\[
\begin{eqnarray}
W(s)&=&\frac {1}{\displaystyle 1 +\frac {s}{k}\left( f_{0}+h_{0}+h_{1}s+h_{2}s^{2}\right) } \\[ 5pt ] &=&\frac {1}{\displaystyle 1 +\frac {f_{0}+h_{0}}{k}s+\frac {h_{1}}{k}s^{2}+\frac {h_{2}}{k}s^{3} } \\[ 5pt ] \end{eqnarray}
\] となるので，\(\displaystyle W_{\mathrm {d}}(s)=\frac {1}{1+\sigma s+\alpha _{2}\sigma ^{2}s^{2}+\alpha _{3}\sigma ^{3}s^{3}}\)と係数比較すると，
\[
\begin{eqnarray}
\frac {f_{0}+h_{0}}{k} &=&\sigma &　・・・・・　④& \\[ 5pt ] \frac {h_{1}}{k}&=&\alpha _{2}\sigma ^{2} &　・・・・・　⑤& \\[ 5pt ] \frac {h_{2}}{k}&=& \alpha _{3}\sigma ^{3} &　・・・・・　⑥&\\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)\(\sigma \)を\(\alpha _{2}\)，\(\alpha _{3}\)，\(h_{1}\)，\(h_{2}\)を用いて表す
\(⑥÷⑤\)より，
\[
\begin{eqnarray}
\frac {\displaystyle \frac {h_{2}}{k}}{\displaystyle \frac {h_{1}}{k}} &=&\frac {\alpha _{3}\sigma ^{3}}{\alpha _{2}\sigma ^{2}} \\[ 5pt ] \frac {h_{2}}{h_{1}} &=&\frac {\alpha _{3}\sigma }{\alpha _{2}} \\[ 5pt ] \sigma &=& \frac {\alpha _{2}h_{2}}{\alpha _{3}h_{1}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)制御定数\(k\)を求める式を\(\alpha _{2}\)，\(h_{1}\)，\(\sigma \)を用いて表す
⑤より，
\[
k=\frac {h_{1}}{\alpha _{2}\sigma ^{2}}
\] と求められる。

(5)制御定数\(f_{0}\)を求める式を\(k\)，\(h_{0}\)，\(\sigma \)を用いて表す
④より，
\[
\begin{eqnarray}
\frac {f_{0}+h_{0}}{k} &=&\sigma \\[ 5pt ] f_{0}+h_{0}&=&k\sigma \\[ 5pt ] f_{0}&=&k\sigma -h_{0} \\[ 5pt ] \end{eqnarray}
\] と求められる。