《理論》〈電子回路〉[H30:問7]バイポーラトランジスタを用いた増幅回路に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，バイポーラトランジスタを用いた増幅回路に関する記述である。文中の\(\fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$}\)に当てはまる最も適切なものを解答群の中から選べ。

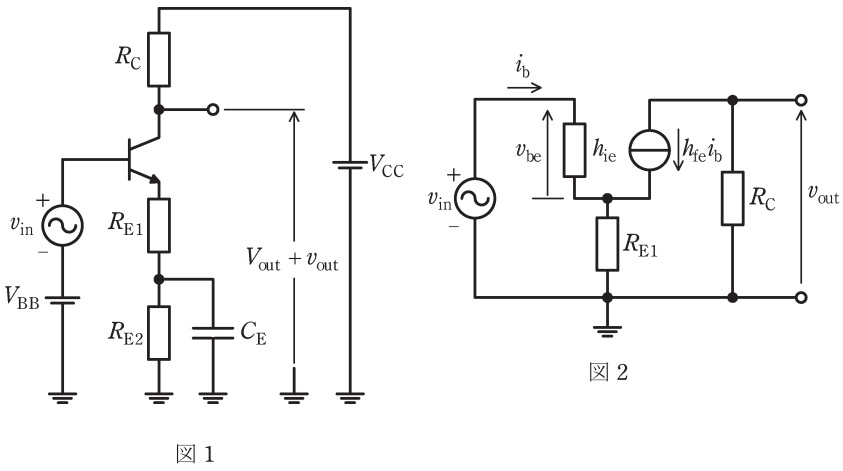
図1の増幅回路は，使用する周波数帯域において容量\( \ C_{\mathrm {E}} \ \)のインピーダンスが十分に小さく短絡とみなせるとき，図2の小信号等価回路で表される。ここで\( \ h_{\mathrm {ie}} \ \)及び\( \ h_{\mathrm {fe}} \ \)はそれぞれエミッタ接地されたバイポーラトランジスタの入力インピーダンスと電流増幅率である。

図2においてトランジスタのベース－エミッタ間電圧\( \ v_{\mathrm {be}} \ \)及び\( \ R_{\mathrm {E1}} \ \)の両端の電圧は，電流\( \ i_{\mathrm {b}} \ \)を用いてそれぞれ\(\fbox {　 （１） 　}\)及び\(\fbox {　 （２） 　}\)と表される。これらの電圧の和は入力電圧\( \ v_{\mathrm {in}} \ \)となることから，電流\( \ i_{\mathrm {b}} \ \)は入力電圧を用いて\(\fbox {　 （３） 　}\)と表される。電流\( \ i_{\mathrm {b}} \ \)は増幅回路の入力電流であるから，増幅回路の入力インピーダンス\( \ \displaystyle \frac {v_{\mathrm {in}}}{i_{\mathrm {b}}} \ \)は\(\fbox {　 （４） 　}\)となる。一方，出力電圧\( \ v_{\mathrm {out}} \ \)は\( \ v_{\mathrm {out}}=-R_{\mathrm {C}}h_{\mathrm {fe}}i_{\mathrm {b}} \ \)であるから，\( \ i_{\mathrm {b}}=\fbox {　 （３） 　}\)を代入することにより，増幅回路の電圧利得\( \ \displaystyle \frac {v_{\mathrm {out}}}{v_{\mathrm {in}}} \ \)は\(\fbox {　 （５） 　}\)となる。

〔問7の解答群〕
\[
\begin{eqnarray}
&（イ）&　h_{\mathrm {ie}}+R_{\mathrm {E1}}\left( 1+h_{\mathrm {fe}}\right)　　　&（ロ）&　\frac {h_{\mathrm {fe}}R_{\mathrm {C}}}{h_{\mathrm {ie}}+R_{\mathrm {E1}}\left( 1+h_{\mathrm {fe}}\right) }　　　&（ハ）&　h_{\mathrm {ie}}i_{\mathrm {b}} \\[ 5pt ] &（ニ）&　\frac {-h_{\mathrm {fe}}R_{\mathrm {C}}}{h_{\mathrm {ie}}+R_{\mathrm {E1}}\left( 1+h_{\mathrm {fe}}\right) }　　　&（ホ）&　\frac {v_{\mathrm {in}}}{h_{\mathrm {ie}}+R_{\mathrm {E1}}\left( 1+h_{\mathrm {fe}}\right) }　　　&（ヘ）&　\left[ h_{\mathrm {ie}}+R_{\mathrm {E1}}\left( 1+h_{\mathrm {fe}}\right) \right] v_{\mathrm {in}} \\[ 5pt ] &（ト）&　h_{\mathrm {ie}}　　　&（チ）&　R_{\mathrm {E1}}\left( 1+h_{\mathrm {fe}}\right) i_{\mathrm {b}}　　　　&（リ）&　\frac {v_{\mathrm {in}}}{h_{\mathrm {ie}}} \\[ 5pt ] &（ヌ）&　h_{\mathrm {ie}}+R_{\mathrm {E1}}　　　　&（ル）&　v_{\mathrm {in}}　　　&（ヲ）&　\frac {-h_{\mathrm {fe}}R_{\mathrm {C}}}{h_{\mathrm {ie}}} \\[ 5pt ] &（ワ）&　\frac {i_{\mathrm {b}}}{h_{\mathrm {ie}}}　　　&（カ）&　R_{\mathrm {E1}}i_{\mathrm {b}}　　　&（ヨ）&　\frac {i_{\mathrm {b}}}{R_{\mathrm {E1}}\left( 1+h_{\mathrm {fe}}\right) } \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

バイポーラトランジスタの小信号等価回路からの出題です。三種ではあまり出題されない分野であり，参考書等で\(h\)パラメータや等価回路について詳しく記載されているものがありますが，ほとんどが回路の数値計算で解けてしまうものが多いので，慣れてしまえば比較的容易に解けるようになると思います。

【解答】

(1)解答：ハ
\( \ h_{\mathrm {ie}} \ \)に流れる電流は\( \ i_{\mathrm {b}} \ \)であるから，ベース－エミッタ間電圧\( \ v_{\mathrm {be}} \ \)は，
\[
\begin{eqnarray}
v_{\mathrm {be}}&=&h_{\mathrm {ie}}i_{\mathrm {b}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：チ
\( \ R_{\mathrm {E1}} \ \)に流れる電流\( \ i_{\mathrm {R}} \ \)は，
\[
\begin{eqnarray}
i_{\mathrm {R}}&=&i_{\mathrm {b}}+h_{\mathrm {fe}}i_{\mathrm {b}} \\[ 5pt ] &=&\left( 1+h_{\mathrm {fe}}\right) i_{\mathrm {b}} \\[ 5pt ] \end{eqnarray}
\] であるから，\( \ R_{\mathrm {E1}} \ \)の両端の電圧\( \ v_{\mathrm {R}} \ \)は，
\[
\begin{eqnarray}
v_{\mathrm {R}}&=&R_{\mathrm {E}}i_{\mathrm {R}} \\[ 5pt ] &=&R_{\mathrm {E1}}\left( 1+h_{\mathrm {fe}}\right) i_{\mathrm {b}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ホ
ベース－エミッタ間電圧\( \ v_{\mathrm {be}} \ \)と\( \ R_{\mathrm {E1}} \ \)の両端の電圧\( \ v_{\mathrm {R}} \ \)の合計が入力電圧\( \ v_{\mathrm {in}} \ \)であるから，
\[
\begin{eqnarray}
v_{\mathrm {in}}&=&v_{\mathrm {be}}+v_{\mathrm {R}} \\[ 5pt ] &=&h_{\mathrm {ie}}i_{\mathrm {b}}+R_{\mathrm {E1}}\left( 1+h_{\mathrm {fe}}\right) i_{\mathrm {b}} \\[ 5pt ] &=&\left[ h_{\mathrm {ie}}+R_{\mathrm {E1}}\left( 1+h_{\mathrm {fe}}\right) \right] i_{\mathrm {b}} \\[ 5pt ] i_{\mathrm {b}}&=&\frac {v_{\mathrm {in}}}{h_{\mathrm {ie}}+R_{\mathrm {E1}}\left( 1+h_{\mathrm {fe}}\right) } \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：イ
(3)より，
\[
\begin{eqnarray}
i_{\mathrm {b}}&=&\frac {v_{\mathrm {in}}}{h_{\mathrm {ie}}+R_{\mathrm {E1}}\left( 1+h_{\mathrm {fe}}\right) } \\[ 5pt ] \frac {v_{\mathrm {in}}}{i_{\mathrm {b}}}&=&h_{\mathrm {ie}}+R_{\mathrm {E1}}\left( 1+h_{\mathrm {fe}}\right) \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ニ
出力電圧\( \ v_{\mathrm {out}} \ \)の導出式から，
\[
\begin{eqnarray}
v_{\mathrm {out}}&=&-R_{\mathrm {C}}h_{\mathrm {fe}}i_{\mathrm {b}} \\[ 5pt ] &=&-R_{\mathrm {C}}h_{\mathrm {fe}}\cdot \frac {v_{\mathrm {in}}}{h_{\mathrm {ie}}+R_{\mathrm {E1}}\left( 1+h_{\mathrm {fe}}\right) } \\[ 5pt ] \frac {v_{\mathrm {out}}}{v_{\mathrm {in}}}&=&\frac {-h_{\mathrm {fe}}R_{\mathrm {C}}}{h_{\mathrm {ie}}+R_{\mathrm {E1}}\left( 1+h_{\mathrm {fe}}\right) } \\[ 5pt ] \end{eqnarray}
\] と求められる。