《理論》〈電子理論〉[R02:問7]n形半導体内の電子による電気伝導に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，半導体内の電気伝導に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。なお，電子の電荷量の大きさを$ \ e \ $とする。

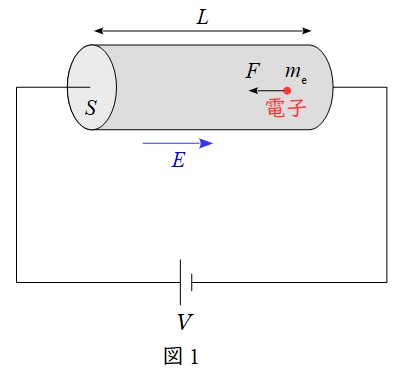
断面積が$ \ S \ $，長さが$ \ L \ $の円柱の$ \ \mathrm {n} \ $形半導体の両端に，大きさが$ \ V \ $の直流電圧を加えた。電圧によって半導体中に一様な電界が形成されるとすると，その電界$ \ E \ $の大きさは$ \ E= \ \fbox {　（１）　} \ $であり，電子は，力の大きさ$ \ F= \ \fbox {　（２）　} \ $で加速される。電子の有効質量を$ \ m_{\mathrm {e}} \ $とすると，加速度の大きさは$ \ \ \fbox {　（３）　} \ $となる。半導体中で加速された電子は散乱を受けて加速が弱まり，最終的に一定の速度$ \ v \ $で運動する定常状態となる。散乱により減速する向きに働く力の大きさは$ \ v \ $に比例し，その比例定数を$ \ \displaystyle \frac {m_{\mathrm {e}}}{\tau } \ $と仮定すると，力の釣り合いの関係式から，$ \ v \ $と電圧$ \ V \ $の関係が，$ \ e \ $，$ \ m_{\mathrm {e}} \ $，$ \ \tau \ $及び$ \ L \ $を用いて，$ \ v= \ \fbox {　（４）　} \ V \ $と表される。なお，$ \ \tau \ $は電子が散乱を受けるまでの時間の目安となる。

半導体中の電子濃度を$ \ n \ $とすると，この半導体を流れる電流$ \ I \ $は，電圧$ \ V \ $と，$ \ e \ $，$ \ m_{\mathrm {e}} \ $，$ \ \tau \ $，$ \ S \ $，$ \ L \ $等を用いて，$ \ I= \ \fbox {　（５）　} \ $と表すことができる。

〔問7の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {e}{m_{\mathrm {e}}\tau L}　　　　　　&（ロ）&　\frac {V}{L}　　　　　　&（ハ）&　\frac {nm_{\mathrm {e}}S}{\tau L}V \\[ 5pt ] &（ニ）&　\frac {eV}{2m_{\mathrm {e}}L}　　　　　　&（ホ）&　\frac {eV}{L}　　　　　　&（ヘ）&　\frac {e\tau }{m_{\mathrm {e}}L} \\[ 5pt ] &（ト）&　\frac {V}{2L}　　　　　　&（チ）&　\frac {e^{2}n\tau S}{m_{\mathrm {e}}L}V　　　　　　&（リ）&　\frac {eL}{m_{\mathrm {e}}V} \\[ 5pt ] &（ヌ）&　\frac {L}{V}　　　　　　&（ル）&　\frac {en\tau S}{m_{\mathrm {e}}L}V　　　　　　&（ヲ）&　\frac {eV}{L^{2}} \\[ 5pt ] &（ワ）&　\frac {eV}{m_{\mathrm {e}}L}　　　　　　&（カ）&　\frac {L}{eV}　　　　　　&（ヨ）&　\frac {m_{\mathrm {e}}}{e\tau L} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

半導体内の電子の運動に関する問題です。電磁気の知識があれば，比較的容易に解けると思います。
電界中の電子の運動に関する内容は$ \ 3 \ $種のテキストにも記載がある内容であると思いますが，なぜか$ \ 3 \ $種での出題が少なく$ \ 2 \ $種では出題されやすい傾向があります。
平成28年問4にも半導体内の電気伝導に関する問題が出題されているので，合わせて確認しておきましょう。

1.静電界中の働く力$ \ F \ $と電界$ \ E \ $の関係
静電界中の電荷$ \ q \ \mathrm {[C]} \ $に電界$ \ E \ \mathrm {[V/m]} \ $がかかっているとき，電荷に働く力$ \ F \ \mathrm {[N]} \ $の大きさは，
\[
\begin{eqnarray}
F &=&qE \\[ 5pt ] \end{eqnarray}
\] で求められます。

2.平行平板コンデンサ内の電界$ \ E \ $
極板間の距離$ \ d \ \mathrm {[m]} \ $の平行平板コンデンサに電圧$ \ V \ \mathrm {[V]} \ $をかけた時，平行平板コンデンサ内の電界$ \ E \ \mathrm {[V/m]} \ $は，
\[
\begin{eqnarray}
E &=&\frac {V}{d} \\[ 5pt ] \end{eqnarray}
\] となります。

3.運動方程式
質量$ \ m \ \mathrm {[kg]} \ $の物体に力$ \ F \ \mathrm {[N]} \ $がかかっている時，この物体にかかる加速度$ \ a \ \mathrm {[m/s^{2}]} \ $との間には，
\[
\begin{eqnarray}
F &=&ma \\[ 5pt ] \end{eqnarray}
\] の関係があります。

4.半導体中の電流$ \ I \ $と電流密度$ \ J \ $
断面積$ \ S \ \mathrm {[m^{2}]} \ $の半導体に一様に電流が流れるとします。
半導体中の電子の電荷を$ \ e \ \mathrm {[C]} \ $，電子濃度を$ \ n \ \mathrm {[m^{-3}]} \ $，平均速度を$ \ v \ \mathrm {[m/s]} \ $とすると，電流密度$ \ J \ \mathrm {[A/m^{2}]} \ $は，
\[
\begin{eqnarray}
J&=&evn \\[ 5pt ] \end{eqnarray}
\] となり，電流$ \ I \ \mathrm {[A]} \ $は，
\[
\begin{eqnarray}
I &=& JS \\[ 5pt ] &=& evnS \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：ロ
円柱の$ \ \mathrm {n} \ $形半導体に電圧をかけたときのイメージを図1に示す。
ワンポイント解説「2.平行平板コンデンサ内の電界$ \ E \ $」の通り，長さ$ \ L \ $に直流電圧$ \ V \ $をかけたときの電界$ \ E \ $の大きさは，
\[
\begin{eqnarray}
E &=&\frac {V}{L} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ホ
ワンポイント解説「1.静電界中の働く力$ \ F \ $と電界$ \ E \ $の関係」の通り，電子にかかる力の大きさ$ \ F \ $は，
\[
\begin{eqnarray}
F &=&eE \\[ 5pt ] &=&\frac {eV}{L} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ワ
ワンポイント解説「3.運動方程式」の通り，電子の有効質量を$ \ m_{\mathrm {e}} \ $とすると，加速度の大きさ$ \ a \ $は，
\[
\begin{eqnarray}
a &=&\frac {F}{m_{\mathrm {e}}} \\[ 5pt ] &=&\frac {eV}{m_{\mathrm {e}}L} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ヘ
題意の通り，散乱により減速する向きに働く力の大きさは速度$ \ v \ $に比例し，その比例定数は$ \ \displaystyle \frac {m_{\mathrm {e}}}{\tau } \ $であるから，
\[
\begin{eqnarray}
F =\frac {eV}{L}&=&\frac {m_{\mathrm {e}}}{\tau }v \\[ 5pt ] v&=&\frac {eV}{L}\cdot \frac {\tau }{m_{\mathrm {e}}} \\[ 5pt ] &=&\frac {e\tau }{m_{\mathrm {e}}L}V \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：チ
ワンポイント解説「4.半導体中の電流$ \ I \ $と電流密度$ \ J \ $」の通り，電流$ \ I \ $は，
\[
\begin{eqnarray}
I &=& evnS \\[ 5pt ] &=& e\cdot \frac {e\tau }{m_{\mathrm {e}}L}V \cdot nS \\[ 5pt ] &=& \frac {e^{2}n\tau S}{m_{\mathrm {e}}L}V \\[ 5pt ] \end{eqnarray}
\] と求められる。