《電力・管理》〈配電〉[H26:問4]高圧配電系統の電圧降下に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

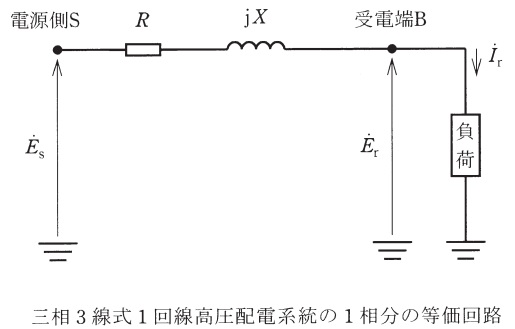
図に示す等価回路の三相3線式1回線の高圧配電系統がある。電源側\(\mathrm {S}\)点の線間電圧\(6.93 \ \mathrm {kV}\)，1線当たりの抵抗\(5 \ \Omega \)，リアクタンス\(7 \ \Omega \)であるとき，次の問に答えよ。ただし，負荷は三相抵抗負荷とする。

(1)　電源側の相電圧\({\dot E}_{\mathrm {s}}\)，受電端の相電圧\({\dot E}_{\mathrm {r}}\)，負荷電流\({\dot I}_{\mathrm {r}}\)のベクトルを図示せよ。

(2)　負荷電流が\(50 \ \mathrm {A}\)流れた際の受電端の線間電圧\(\sqrt {3} \left| {\dot E}_{\mathrm {r}}\right| \left[ \mathrm {kV}\right] \)を上記(1)で表したベクトル図の関係式から求めよ。ただし，当該線路に他の負荷はなく，漏れ電流等は無視できるものとする。

(3)　受電端\(\mathrm {B}\)点において線路の電圧降下率が\(10 \ ％\)となる三相抵抗負荷電力\(\left[ \mathrm {kW}\right] \)及びそのときの負荷電流\(\left[ \mathrm {A}\right] \)を求めよ。

【ワンポイント解説】

本問の場合は電圧降下の簡略式を使用して良いと書いていないので，(3)では電圧降下率の定義から正確に求める必要があります。計算がやや複雑になってしまいますが，考え方はそれほど難しい問題ではないため，よく理解するようにしましょう。

1.電圧降下率\(\varepsilon \)
送電側の相電圧を相電圧\({\dot E}_{\mathrm {s}}\)，受電端の相電圧\({\dot E}_{\mathrm {r}}\)とした時，電圧降下率\(\varepsilon \)は，
\[
\begin{eqnarray}
\varepsilon &=&\frac {\left| {\dot E}_{\mathrm {s}}\right| -\left| {\dot E}_{\mathrm {r}}\right| }{\left| {\dot E}_{\mathrm {r}}\right| }\times 100 \ [％] \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)電源側の相電圧\({\dot E}_{\mathrm {s}}\)，受電端の相電圧\({\dot E}_{\mathrm {r}}\)，負荷電流\({\dot I}_{\mathrm {r}}\)のベクトル
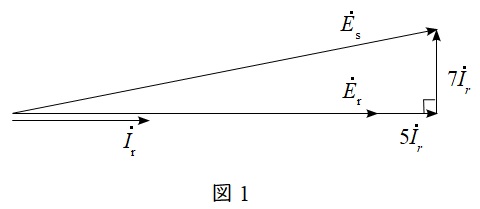
題意より，負荷は三相抵抗負荷であるから，受電端の相電圧\({\dot E}_{\mathrm {r}}\)と負荷電流\({\dot I}_{\mathrm {r}}\)の位相は等しくなる。したがって，\({\dot E}_{\mathrm {r}}\)を基準としてベクトル図を描くと図1のようになる。

(2)負荷電流が\(50 \ \mathrm {A}\)流れた際の受電端の線間電圧\(\sqrt {3} \left| {\dot E}_{\mathrm {r}}\right| \left[ \mathrm {kV}\right] \)
題意より，電源側\(\mathrm {S}\)点の線間電圧\(6.93 \ \mathrm {kV}\)であるから，相電圧\({\dot E}_{\mathrm {s}}\)の大きさは，
\[
\begin{eqnarray}
\left| {\dot E}_{\mathrm {s}}\right| &=&\frac {6.93}{\sqrt {3}} \\[ 5pt ] &≒&4.0010 \ [ \mathrm {kV} ] \\[ 5pt ] \end{eqnarray}
\] となる。また，\({\dot I}_{\mathrm {r}}=50 \ \mathrm {A}\)であるから，線路の抵抗及びリアクタンス降下の大きさはそれぞれ
\[
\begin{eqnarray}
5\left| {\dot I}_{\mathrm {r}}\right| &=&5\times 50 \\[ 5pt ] &=&250 \ [ \mathrm {V} ] \\[ 5pt ] 7\left| {\dot I}_{\mathrm {r}}\right| &=&7\times 50 \\[ 5pt ] &=&350 \ [ \mathrm {V} ] \\[ 5pt ] \end{eqnarray}
\] となる。よって，これらを図1のベクトル図に当てはめると図2のようになる。三平方の定理より\({\dot E}_{\mathrm {r}}\)の大きさを求めると，
\[
\begin{eqnarray}
\left( 4.0010\times 10^{3}\right) ^{2} &=&\left( \left| {\dot E}_{\mathrm {r}}\right| +250 \right) ^{2} +350^{2} \\[ 5pt ] 16008001 &=&\left| {\dot E}_{\mathrm {r}}\right| ^{2} +500\left| {\dot E}_{\mathrm {r}}\right| +62500 +122500 \\[ 5pt ] \left| {\dot E}_{\mathrm {r}}\right| ^{2} +500\left| {\dot E}_{\mathrm {r}}\right| -15823001 &=&0 \\[ 5pt ] \left| {\dot E}_{\mathrm {r}}\right| &=&-250±\sqrt {250^{2}+15823001} \\[ 5pt ] &≒&3735.7，-4235.7（不適）　→　3.7357 \ \mathrm {[kV]} \\[ 5pt ] \end{eqnarray}
\] となるので，受電端の線間電圧の大きさは，
\[
\begin{eqnarray}
\sqrt {3}\left| {\dot E}_{\mathrm {r}}\right| &=&\sqrt {3}\times 3.7357 \\[ 5pt ] &≒&6.4704　→　6.47 \ \mathrm {[kV]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)受電端\(\mathrm {B}\)点において線路の電圧降下率が\(10 \ ％\)となる三相抵抗負荷電力\(\left[ \mathrm {kW}\right] \)及びそのときの負荷電流\(\left[ \mathrm {A}\right] \)
ワンポイント解説「1.電圧降下率\(\varepsilon \)」より，
\[
\begin{eqnarray}
0.1 &=&\frac {\left| {\dot E}_{\mathrm {s}}\right| -\left| {\dot E}_{\mathrm {r}}\right| }{\left| {\dot E}_{\mathrm {r}}\right| } \\[ 5pt ] 0.1 &=&\frac {4.0010 -\left| {\dot E}_{\mathrm {r}}\right| }{\left| {\dot E}_{\mathrm {r}}\right| } \\[ 5pt ] \left| {\dot E}_{\mathrm {r}}\right| &=&\frac {4.0010}{1.1} \\[ 5pt ] &≒&3.6373 \ \mathrm {[kV]} \\[ 5pt ] \end{eqnarray}
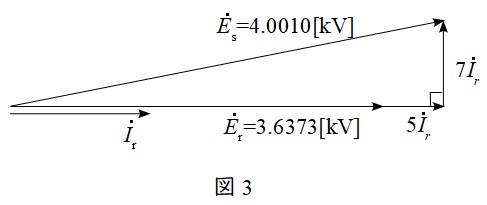
\] であるから，ベクトル図は図3のようになる。三平方の定理により負荷電流の大きさ\(\left| {\dot I}_{\mathrm {r}}\right| \)を求めると，
\[
\begin{eqnarray}
\left( 5\left| {\dot I}_{\mathrm {r}}\right| +3637.3\right) ^{2}+\left( 7\left| {\dot I}_{\mathrm {r}}\right| \right) ^{2}&=&4001.0^{2} \\[ 5pt ] 74\left| {\dot I}_{\mathrm {r}}\right| ^{2} +36373\left| {\dot I}_{\mathrm {r}}\right| -2778050&=&0 \\[ 5pt ] \left| {\dot I}_{\mathrm {r}}\right| &=& \frac {-36373±\sqrt {36373^{2}+4\times 74\times 2778050}}{2\times 74} \\[ 5pt ] &≒& 67.189，-558.72（不適）　→　67.2 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。また，三相抵抗負荷電力\(P\)は，
\[
\begin{eqnarray}
P &=&3\left| {\dot E}_{\mathrm {r}}\right| \left| {\dot I}_{\mathrm {r}}\right| \\[ 5pt ] &=&3\times 3.6373\times 67.189 \\[ 5pt ] &≒&733.16　→　733 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。