《電力・管理》〈配電〉[H27:問3]配電線の負荷による電圧降下に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

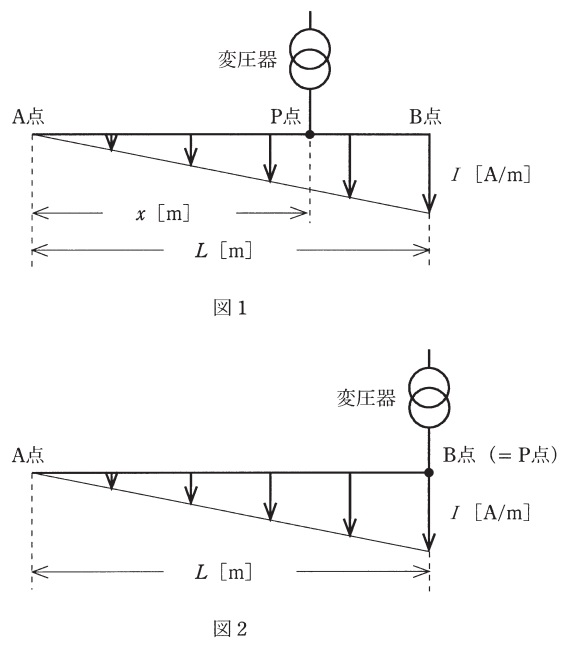
図1に示すように，\(\mathrm {A}\)点から\(\mathrm {B}\)点に行くほど直線的に負荷密度が大きくなる低圧負荷が分布している配電線路(全長\(L \ \mathrm {[m]}\))の途中に，変圧器を設置し給電するとき，次の問に答えよ。

ただし，配電線路の線路特性は均一として，給電点(\(\mathrm {P}\)点)電圧は一定であり，負荷は抵抗負荷とする。また，線路の電圧降下は抵抗分(単位長さ当たりの等価抵抗を\(R \ \mathrm {[\Omega /m]}\)とする。)のみを考慮することとし，図中の\(I \ \mathrm {[A/m]}\)は，\(\mathrm {B}\)点における負荷密度とする。

(1)　変圧器の設置地点\(\mathrm {P}\)から，\(\mathrm {A}\)点及び\(\mathrm {B}\)点までのそれぞれの電圧降下が等しくなるようにしたい。\(\mathrm {P}\)点は，\(\mathrm {A}\)点から何メートルの場所にすればよいかを考える。次の各問に答えよ。

a.\(\mathrm {A}\)点と\(\mathrm {P}\)点の間の距離を\(x \ \mathrm {[m]}\)として，\(\mathrm {P}\)点から\(\mathrm {A}\)点の間の電圧降下\(V_{\mathrm {A}} \ \mathrm {[V]}\)を求めよ。

b.\(\mathrm {P}\)点から\(\mathrm {B}\)点の間の電圧降下\(V_{\mathrm {B}} \ \mathrm {[V]}\)を求めよ。

c.\(V_{\mathrm {A}}=V_{\mathrm {B}}\)となる場合の\(\mathrm {A}\)点と\(\mathrm {P}\)点の間の距離\(x \ \mathrm {[m]}\)を求めよ。

(2)　上記(1)で求めた地点に変圧器を設置する場合の\(\mathrm {P}\)点から\(\mathrm {A}\)点までの電圧降下の値は，図2に示すように\(\mathrm {B}\)点に変圧器を設置した場合の\(\mathrm {P}\)点(\( =\mathrm {B}\)点)から\(\mathrm {A}\)点までの電圧降下の値の何\([％]\)になるのか計算せよ。

【ワンポイント解説】

計算がやや複雑ですが，過去に類題も出題されており，積分計算に慣れてしまえば，比較的容易に解けると思います。計算問題は過去問の類題が出題されることが多いです。

【解答】

(1)a.\(\mathrm {P}\)点から\(\mathrm {A}\)点の間の電圧降下\(V_{\mathrm {A}} \ \mathrm {[V]}\)
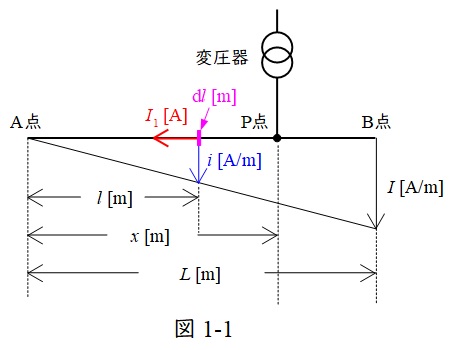
図1-1のように\(\mathrm {A}\)点から距離\(l\)(\(l ＜ x\))の地点の負荷密度\(i\)とすると，その大きさは，
\[
\begin{eqnarray}
i&=& \frac {l}{L}I \\[ 5pt ] &=& \frac {I}{L}l \\[ 5pt ] \end{eqnarray}
\] となる。また，\(\mathrm {A}\)点から距離\(l\)の地点の線路電流の大きさ\(I_{1}\)は，\(\mathrm {A}\)点からの負荷密度の大きさの合計値であるから，
\[
\begin{eqnarray}
I_{1}&=& \int ^{l}_{0}i \mathrm {d}l \\[ 5pt ] &=& \int ^{l}_{0}\frac {I}{L}l \mathrm {d}l \\[ 5pt ] &=& \frac {I}{L}\left[ \frac {l^{2}}{2}\right] ^{l}_{0} \\[ 5pt ] &=& \frac {I}{2L}l^{2} \\[ 5pt ] \end{eqnarray}
\] となる。\(\mathrm {A}\)点から距離\(l\)の地点の微小区間における電圧降下\(\mathrm {d}V_{\mathrm {A}}\)は，
\[
\begin{eqnarray}
\mathrm {d}V_{\mathrm {A}}&=& R\mathrm {d}l\cdot I_{1} \\[ 5pt ] &=& \frac {RI}{2L}l^{2}\mathrm {d}l \\[ 5pt ] \end{eqnarray}
\] となるので，\(\mathrm {P}\)点から\(\mathrm {A}\)点の間の電圧降下\(V_{\mathrm {A}}\)は，
\[
\begin{eqnarray}
V_{\mathrm {A}}&=& \int \mathrm {d}V_{\mathrm {A}} \\[ 5pt ] &=& \int ^{x}_{0}\frac {RI}{2L}l^{2}\mathrm {d}l \\[ 5pt ] &=& \frac {RI}{2L}\left[ \frac {l^{3}}{3}\right] ^{x}_{0} \\[ 5pt ] &=& \frac {RI}{6L}x^{3} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(1)b.\(\mathrm {P}\)点から\(\mathrm {B}\)点の間の電圧降下\(V_{\mathrm {B}} \ \mathrm {[V]}\)
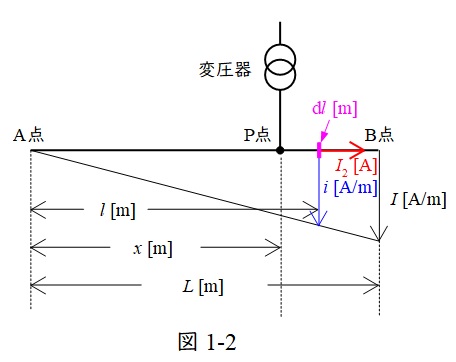
図1-2のように\(\mathrm {A}\)点から距離\(l\)(\(x ＜ l ＜ L\))の地点の負荷密度\(i\)とすると，その大きさは，
\[
\begin{eqnarray}
i&=& \frac {l}{L}I \\[ 5pt ] &=& \frac {I}{L}l \\[ 5pt ] \end{eqnarray}
\] となるので，\(\mathrm {A}\)点から距離\(l\)の地点の線路電流の大きさ\(I_{2}\)は，\(\mathrm {B}\)点からの負荷密度の大きさの合計値であるから，
\[
\begin{eqnarray}
I_{2}&=& \int ^{L}_{l}i \mathrm {d}l \\[ 5pt ] &=& \int ^{L}_{l}\frac {I}{L}l \mathrm {d}l \\[ 5pt ] &=& \frac {I}{L}\left[ \frac {l^{2}}{2}\right] ^{L}_{l} \\[ 5pt ] &=& \frac {I}{2L}\left( L^{2}-l^{2}\right) \\[ 5pt ] \end{eqnarray}
\] となるので，\(\mathrm {A}\)点から距離\(l\)の地点の微小区間における電圧降下\(\mathrm {d}V_{\mathrm {B}}\)は，
\[
\begin{eqnarray}
\mathrm {d}V_{\mathrm {B}}&=& R\mathrm {d}l\cdot I_{2} \\[ 5pt ] &=& \frac {RI}{2L}\left( L^{2}-l^{2}\right) \mathrm {d}l \\[ 5pt ] \end{eqnarray}
\] となり，\(\mathrm {P}\)点から\(\mathrm {B}\)点の間の電圧降下\(V_{\mathrm {B}}\)は，
\[
\begin{eqnarray}
V_{\mathrm {B}}&=& \int \mathrm {d}V_{\mathrm {B}} \\[ 5pt ] &=& \int ^{L}_{x}\frac {RI}{2L}\left( L^{2}-l^{2}\right) \mathrm {d}l \\[ 5pt ] &=& \frac {RI}{2L}\left[ L^{2}l -\frac {l^{3}}{3}\right] ^{L}_{x} \\[ 5pt ] &=& \frac {RI}{2L}\left( L^{3} -\frac {L^{3}}{3} -L^{2}x +\frac {x^{3}}{3}\right) \\[ 5pt ] &=& \frac {RI}{6L}\left( 2L^{3} -3L^{2}x +x^{3}\right) \\[ 5pt ] \end{eqnarray}
\] と求められる。

(1)c.\(V_{\mathrm {A}}=V_{\mathrm {B}}\)となる場合の\(\mathrm {A}\)点と\(\mathrm {P}\)点の間の距離\(x \ \mathrm {[m]}\)
(1)a.及び(1)b.より，
\[
\begin{eqnarray}
V_{\mathrm {A}}&=& V_{\mathrm {B}} \\[ 5pt ] \frac {RI}{6L}x^{3}&=& \frac {RI}{6L}\left( 2L^{3} -3L^{2}x +x^{3}\right) \\[ 5pt ] x^{3}&=&2L^{3} -3L^{2}x +x^{3} \\[ 5pt ] 0&=&2L^{3} -3L^{2}x \\[ 5pt ] x&=&\frac {2}{3}L
\end{eqnarray}
\] と求められる。

(2)(1)は\(\mathrm {B}\)点に変圧器を設置した場合の\(\mathrm {P}\)点\(( =\mathrm {B}\)点)から\(\mathrm {A}\)点までの電圧降下の値の何\([％]\)になるか
(1)a.より，\(\displaystyle V_{\mathrm {A}}=\frac {RI}{6L}x^{3}\)であるから，\(\displaystyle x=\frac {2}{3}L\)の時の電圧降下と\(x=L\)の時の電圧降下の比は，
\[
\begin{eqnarray}
\frac {\displaystyle \frac {RI}{6L}\left( \frac {2}{3}L\right) ^{3}}{\displaystyle \frac {RI}{6L}L^{3}}&=& \left( \frac {2}{3}\right) ^{3} \\[ 5pt ] &=& \frac {8}{27} \\[ 5pt ] &≒&0.296　→　29.6 \ [％] \\[ 5pt ] \end{eqnarray}
\] と求められる。