【問題】
【難易度】★★★★★(難しい)
電力円線図と無効電力損失に関して,次の問に答えよ。ただし,計算には全て単位法を用いること。
(1) 短距離の高圧送電線は,対地容量と線路抵抗を無視すると図のような等価回路で表現できる。送受電端の電圧の大きさがともに\( \ 1.0 \ \mathrm {p.u.} \ \)に保たれるとして,送電電力\( \ P\),送電端無効電力\( \ Q_{\mathrm {s}}\),受電端無効電力\( \ Q_{\mathrm {r}} \ \)はそれぞれどのように表されるか。送受電端電圧間の位相差\( \ \delta \ \)(受電端を基準とする)と送電端リアクタンス\( \ X \ \)を用いて表せ。ただし,無効電力は遅れを正とする。
(2) 上記の場合に,送電端複素電力\( \ {\dot S}_{\mathrm {s}}=P+\mathrm {j}Q_{\mathrm {s}} \ \)及び受電端複素電力\( \ {\dot S}_{\mathrm {r}}=P+\mathrm {j}Q_{\mathrm {r}} \ \)が複素平面上で円を描くことを示せ。
(3) 上で求めた二円はそれぞれ送電円,受電円と呼ばれており,一般に複素平面上に表された複素送電電力の線図を電力円線図と呼ぶ。送電線の亘長が\(2\)倍になり,\(X \ \)が\(2\)倍になっても引き続き同一の有効電力を送電する場合,\(\delta \ \)が大きく開くことを送電円を用いて説明せよ。
(4) (3)で記したように\( \ X \ \)を\(2\)倍にした送電線でも同一の有効電力を送電するとき,無効電力損失が\( \ X \ \)を\(2\)倍にする前と比べてどうなるかを送電円,受電円を用いて説明せよ。
(5) 周波数\( \ 50 \ \mathrm {Hz}\),作用インダクタンス\( \ 1.3 \ \mathrm {mH/km} \ \)をもつ\( \ 10 \ \mathrm {km} \ \)一回線の送電線で\( \ 300 \ \mathrm {MW} \ \)を送電する場合について送電円,受電円を描き,\( \ \sin \delta \ \)と無効電力損失\( \ Q_{\mathrm {s}}-Q_{\mathrm {r}} \ \)を算出せよ。単位法は基準電圧\( \ 66 \ \mathrm {kV}\),基準容量\( \ 1000 \ \mathrm {MV\cdot A} \ \)とし,\( \ \pi =3.1416 \ \)とする。

【ワンポイント解説】
この問題自体は電験一種でよく見かけるような問題です。計算量も一種の問題並みと考えてよく,解くのに時間がかかり難易度が高い問題です。しかし,電力円線図の式の導出の方法はほぼ毎回同じような解き方をしますので,解き方を暗記しておけば怖くなくなる問題でもあります。
1.送電線の送電電力\( \ P \ \)
送電端電圧\( \ V_{\mathrm {s}} \),受電端電圧\( \ V_{\mathrm {r}} \),線路のリアクタンス\( \ X \),送受電端の電圧の位相差を\( \ \delta \ \)とした時,送電線の送電電力\( \ P \ \)は,
\[
\begin{eqnarray}
P&=&\frac {V_{\mathrm {s}}V_{\mathrm {r}}}{X}\sin \delta \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
※ 本問でどのように導出されるかマスターして下さい。
2.複素電力\( \ \dot S=P+\mathrm {j}Q \ \)
電圧\( \ V \),電流\( \ I \ \)とした時,送電線の送電電力\( \ \dot S=P+\mathrm {j}Q \ \)は,
遅れ無効電力を正とすると,
\[
\begin{eqnarray}
\dot S=P+\mathrm {j}Q&=&\dot V \overline {\dot I} \\[ 5pt ]
\end{eqnarray}
\]
進み無効電力を正とすると,
\[
\begin{eqnarray}
\dot S=P+\mathrm {j}Q&=&\overline {\dot V}\dot I \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
3.単位法
基準容量を\(P_{\mathrm {B}}\),基準電圧を\(V_{\mathrm {B}}\)とすると,
\[
\begin{eqnarray}
P \ \mathrm {[p.u.]}&=&\frac {P \ \mathrm {[W]}}{P_{\mathrm {B}}} \\[ 5pt ]
V \ \mathrm {[p.u.]}&=&\frac {V \ \mathrm {[V]}}{V_{\mathrm {B}}} \\[ 5pt ]
I \ \mathrm {[p.u.]}&=&\frac {I \ \mathrm {[A]}}{I_{\mathrm {B}}} \\[ 5pt ]
&=&\frac {I \ \mathrm {[A]}}{\displaystyle \frac {P_{\mathrm {B}}}{\sqrt {3}V_{\mathrm {B}}}} \\[ 5pt ]
&=&\frac {\sqrt {3}V_{\mathrm {B}}}{P_{\mathrm {B}}}\cdot I \ \mathrm {[A]} \\[ 5pt ]
Z \ \mathrm {[p.u.]}&=&\frac {Z \ \mathrm {[\Omega ]}}{Z_{\mathrm {B}}} \\[ 5pt ]
&=&\frac {Z \ \mathrm {[\Omega ]}}{\displaystyle \frac {V_{\mathrm {B}}}{\sqrt {3}I_{\mathrm {B}}}} \\[ 5pt ]
&=&\frac {\sqrt {3}}{V_{\mathrm {B}}}I_{\mathrm {B}}\cdot Z \ \mathrm {[\Omega ]} \\[ 5pt ]
&=&\frac {\sqrt {3}}{V_{\mathrm {B}}} \frac {P_{\mathrm {B}}}{\sqrt {3}V_{\mathrm {B}}}\cdot Z \ \mathrm {[\Omega ]} \\[ 5pt ]
&=&\frac {P_{\mathrm {B}}}{V_{\mathrm {B}}^{2}}\cdot Z \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となります。インピーダンスの式は公式として暗記しておきましょう。
【関連する「電気の神髄」記事】
【解答】
(1)送受電端の電圧の大きさがともに\( \ 1.0 \ \mathrm {p.u.} \ \)に保たれるとした時の,送電電力\( \ P\),送電端無効電力\( \ Q_{\mathrm {s}}\),受電端無効電力\( \ Q_{\mathrm {r}} \ \)の値
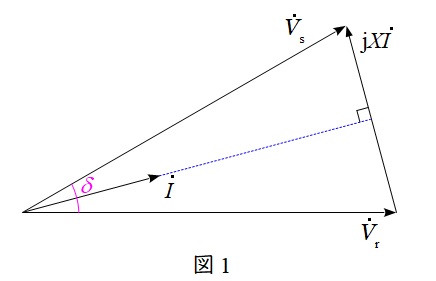
題意に沿ってベクトル図を描くと図1のようになる。図1において,受電電圧\( \ {\dot V}_{\mathrm {r}}=1.0 \ \mathrm {[p.u.]} \)を基準とすると,送電電圧\( \ {\dot V}_{\mathrm {s}} \)は,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {s}}&=&1.0\left( \cos \delta +\mathrm {j}\sin \delta \right) \\[ 5pt ]
&=&\cos \delta +\mathrm {j}\sin \delta \\[ 5pt ]
\end{eqnarray}
\]
となる。送電線を流れる電流\( \ \dot I \ \)は,
\[
\begin{eqnarray}
\dot I&=&\frac {{\dot V}_{\mathrm {s}}-{\dot V}_{\mathrm {r}}}{\mathrm {j}X} \\[ 5pt ]
&=&\frac {\cos \delta +\mathrm {j}\sin \delta -1}{\mathrm {j}X} \\[ 5pt ]
&=&\frac {\mathrm {j}\sin \delta }{\mathrm {j}X}+\frac {\cos \delta -1}{\mathrm {j}X} \\[ 5pt ]
&=&\frac {\sin \delta }{X}+\mathrm {j}\frac {1-\cos \delta }{X} \\[ 5pt ]
\end{eqnarray}
\]
となるので,ワンポイント解説「2.複素電力\( \ \dot S=P+\mathrm {j}Q \ \)」の通り,送電端複素電力\( \ {\dot S}_{\mathrm {s}}=P+\mathrm {j}Q_{\mathrm {s}} \ \)は,
\[
\begin{eqnarray}
P+\mathrm {j}Q_{\mathrm {s}}&=&{\dot V}_{\mathrm {s}}\overline {\dot I} \\[ 5pt ]
&=&\left( \cos \delta +\mathrm {j}\sin \delta \right) \left( \frac {\sin \delta }{X}-\mathrm {j}\frac {1-\cos \delta }{X}\right) \\[ 5pt ]
&=&\left( \frac {\sin \delta \cos \delta }{X}+\frac {\sin \delta }{X}-\frac {\sin \delta \cos \delta }{X}\right) +\mathrm {j}\left( \frac {\sin ^{2}\delta }{X}-\frac {\cos \delta -\cos ^{2}\delta }{X}\right) \\[ 5pt ]
&=&\frac {\sin \delta }{X}+\mathrm {j}\frac {\sin ^{2}\delta +\cos ^{2}\delta -\cos \delta }{X} \\[ 5pt ]
&=&\frac {\sin \delta }{X}+\mathrm {j}\frac {1-\cos \delta }{X} \\[ 5pt ]
\end{eqnarray}
\]
となり,受電端複素電力\( \ {\dot S}_{\mathrm {r}}=P+\mathrm {j}Q_{\mathrm {r}} \ \)は,
\[
\begin{eqnarray}
P+\mathrm {j}Q_{\mathrm {r}}&=&{\dot V}_{\mathrm {r}}\overline {\dot I} \\[ 5pt ]
&=&1.0 \left( \frac {\sin \delta }{X}-\mathrm {j}\frac {1-\cos \delta }{X}\right) \\[ 5pt ]
&=&\frac {\sin \delta }{X}+\mathrm {j}\frac {\cos \delta -1}{X} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
P&=&\frac {\sin \delta }{X} \\[ 5pt ]
Q_{\mathrm {s}}&=&\frac {1-\cos \delta }{X} \\[ 5pt ]
Q_{\mathrm {r}}&=&\frac {\cos \delta -1}{X} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)送電端複素電力\( \ {\dot S}_{\mathrm {s}}=P+\mathrm {j}Q_{\mathrm {s}} \ \)及び受電端複素電力\( \ {\dot S}_{\mathrm {r}}=P+\mathrm {j}Q_{\mathrm {r}} \ \)が複素平面上で円を描くことを示す
(1)の解答より,
\[
\begin{eqnarray}
\sin \delta &=&XP \\[ 5pt ]
\cos \delta &=&1-XQ_{\mathrm {s}} \\[ 5pt ]
\cos \delta &=&1+XQ_{\mathrm {r}} \\[ 5pt ]
\end{eqnarray}
\]
となり,\(\sin ^{2}\delta +\cos ^{2}\delta=1\)であるから,送電端に関して,
\[
\begin{eqnarray}
\sin ^{2}\delta +\cos ^{2}\delta &=&1 \\[ 5pt ]
\left( XP\right) ^{2} +\left( 1-XQ_{\mathrm {s}}\right) ^{2} &=&1 \\[ 5pt ]
\left( XP\right) ^{2} +\left( XQ_{\mathrm {s}}-1\right) ^{2} &=&1 \\[ 5pt ]
P^{2} +\left( Q_{\mathrm {s}}-\frac {1}{X}\right) ^{2} &=&\left( \frac {1}{X}\right) ^{2} \\[ 5pt ]
\end{eqnarray}
\]
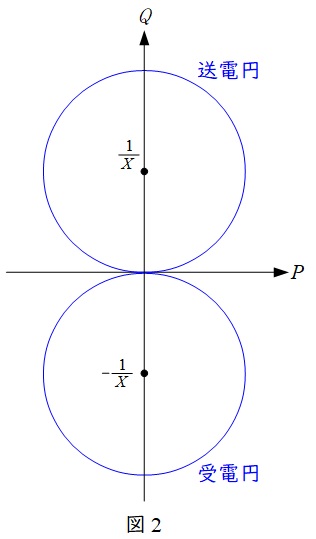
となり,中心が\(\displaystyle \left( 0,\frac {1}{X}\right) \),半径が\(\displaystyle \frac {1}{X}\)の円を描くことになる。
同様に受電端に関して,
\[
\begin{eqnarray}
\sin ^{2}\delta +\cos ^{2}\delta &=&1 \\[ 5pt ]
\left( XP\right) ^{2} +\left( 1+XQ_{\mathrm {r}}\right) ^{2} &=&1 \\[ 5pt ]
\left( XP\right) ^{2} +\left( XQ_{\mathrm {r}}+1\right) ^{2} &=&1 \\[ 5pt ]
P^{2} +\left( Q_{\mathrm {r}}+\frac {1}{X}\right) ^{2} &=&\left( \frac {1}{X}\right) ^{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,中心が\(\displaystyle \left( 0,-\frac {1}{X}\right) \),半径が\(\displaystyle \frac {1}{X}\)の円を描くことになる。
(3)\(X \ \)が\(2\)倍になっても引き続き同一の有効電力を送電する場合,\(\delta \ \)が大きく開くことの説明
\(X \ \)が\(2\)倍になった時,送電端の式は
\[
\begin{eqnarray}
P^{2} +\left( Q_{\mathrm {s}}-\frac {1}{2X}\right) ^{2} &=&\left( \frac {1}{2X}\right) ^{2} \\[ 5pt ]
\end{eqnarray}
\]
となるので,中心が\(\displaystyle \left( 0,\frac {1}{2X}\right) \),半径が\(\displaystyle \frac {1}{2X}\)の円を描くことになる。
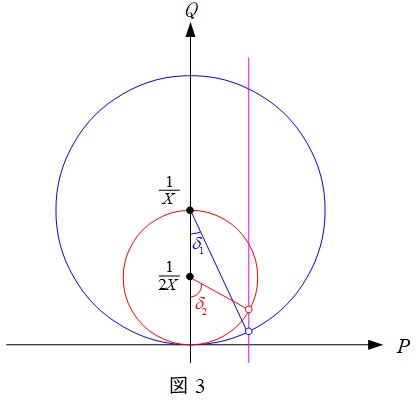
これより,電力円線図は図3のようになる。
相差角が\(0°\)の時,(1)より,\(P=0\),\(Q_{\mathrm {s}}=0\)となり,そこから相差角が増大すると,運転点が円周を左回りに動くことになる。同一の有効電力を送電する場合,\(X \ \)の時の相差角を\( \ \delta _{1} \),\(2X \ \)の時の相差角を\( \ \delta _{2} \ \)とすると,それぞれ図3に示した角度となる。
よって,\( \ \delta _{1}<\delta _{2} \ \)となることが分かる。
(4)\( \ X \ \)を\(2\)倍にした送電線でも同一の有効電力を送電するとき,無効電力損失が\( \ X \ \)を\(2\)倍にする前と比べてどうなるか
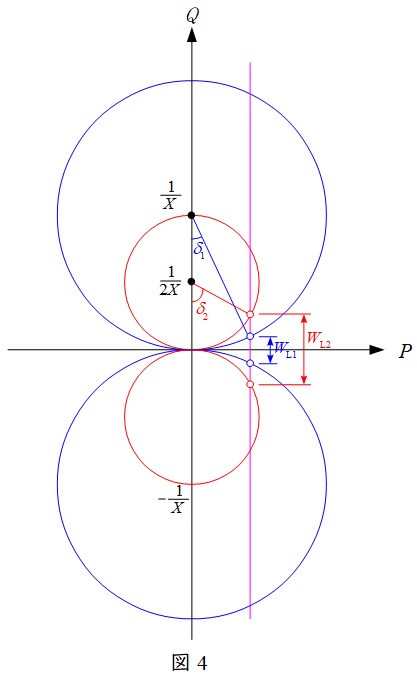
受電円も含めた電力円線図を図4に示す。
無効電力損失は\( \ Q_{\mathrm {s}}-Q_{\mathrm {r}} \ \)であるから,送電線のリアクタンスが\(X\)の時の無効電力損失は図4の\( \ W_{\mathrm {L1}} \ \),リアクタンスが\(2X\)の時の無効電力損失は図4の\( \ W_{\mathrm {L2}} \ \)となり,\( \ X \ \)を\(2\)倍にした送電線の方が無効電力損失は大きくなる。
(5)送電円,受電円を描き,\( \ \sin \delta \ \)と無効電力損失\( \ Q_{\mathrm {s}}-Q_{\mathrm {r}} \ \)を導出
ワンポイント解説「3.単位法」により与えられた電力及びリアクタンスを単位法で表すと,
\[
\begin{eqnarray}
P &=&\frac {P \ \mathrm {[W]}}{P_{\mathrm {B}}} \\[ 5pt ]
&=&\frac {300\times 10^{6}}{1000\times 10^{6}} \\[ 5pt ]
&=&0.3 \ \mathrm {[p.u.]} \\[ 5pt ]
X&=&\frac {P_{\mathrm {B}}}{V_{\mathrm {B}}^{2}}\cdot X \ \mathrm {[\Omega ]} \\[ 5pt ]
&=&\frac {1000\times 10^{6}}{\left( 66\times 10^{3}\right) ^{2}}\times \left[ 2\pi \times 50\times \left( 1.3\times 10^{-3}\right) \times 10\right] \\[ 5pt ]
&≒&0.93758 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となる。
(1)より,\(\sin \delta \)は,
\[
\begin{eqnarray}
\sin \delta &=&XP \\[ 5pt ]
&=&0.93758\times 0.3 \\[ 5pt ]
&≒&0.28127 → 0.281 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となり,無効電力損失\( \ Q_{\mathrm {s}}-Q_{\mathrm {r}} \ \)は,
\[
\begin{eqnarray}
Q_{\mathrm {s}}-Q_{\mathrm {r}} &=&\frac {1-\cos \delta }{X}-\frac {\cos \delta -1}{X} \\[ 5pt ]
&=&\frac {2\left( 1-\cos \delta \right) }{X} \\[ 5pt ]
&=&\frac {2\left( 1-\sqrt {1-\sin ^{2}\delta } \right) }{X} \\[ 5pt ]
&=&\frac {2\times \left( 1-\sqrt {1-0.28127^{2} } \right) }{0.93758} \\[ 5pt ]
&≒&0.086118 → 0.0861 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
求められる。送電円の中心\(\displaystyle \frac {1}{X}\)は,
\[
\begin{eqnarray}
\frac {1}{X} &=&\frac {1}{0.93758} \\[ 5pt ]
&≒&1.0666 → 1.07 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
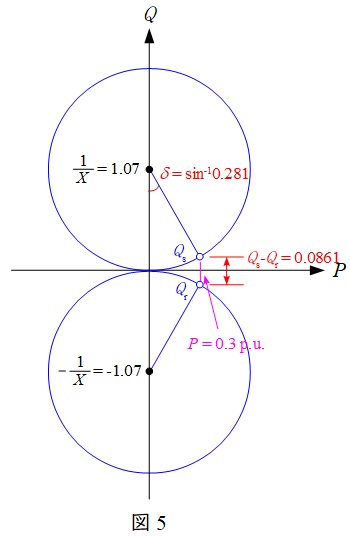
となるので,電力円線図は図5のようになる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは