Contents
【問題】
【難易度】★★★★☆(やや難しい)
配電系統の電力損失を低減することはエネルギー資源の効率的な活用に有用である。次の問に答えよ。
(1) 柱上変圧器を重負荷地点近傍に設置することは,電力損失を低減する方策の一つである。これ以外の配電系統の電力損失低減策を三つ述べよ。
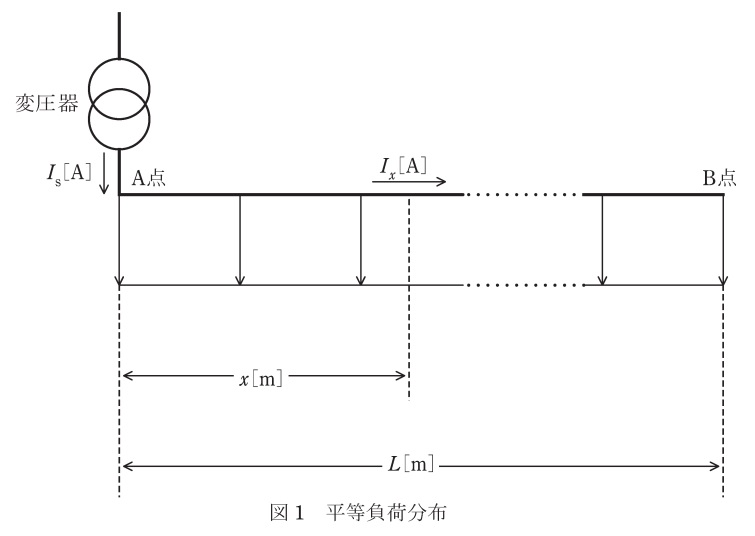
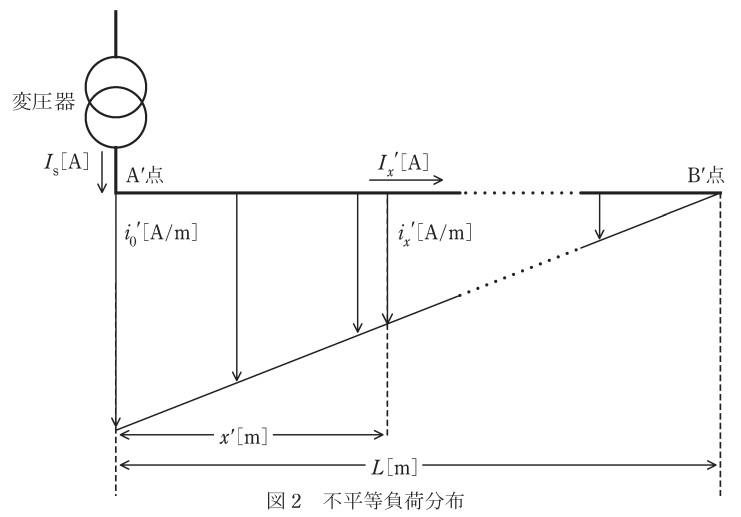
(2) 柱上変圧器を重負荷地点近傍に設置することによる電力損失低減効果について,a)平等負荷分布(各地点での負荷電流が同じ)及びb)不平等負荷分布における電力損失を求めることにより,b)がa)より小さくなることを示したい。
a) 図1に示すように,平等負荷分布である単相\( \ 2 \ \)線式の低圧配電系統において,電線こう長\( \ L \ \mathrm {[m]} \ \),\( \ \mathrm {A} \ \)点から\( \ x \ \mathrm {[m]} \ \)だけ離れた地点の線路電流\( \ I_{\mathrm {x}} \ \mathrm {[A]} \ \)を求めたうえで,低圧配電線の全区間の電力損失を\( \ I_{\mathrm {s}} \ \),\( \ L \ \),\( \ r \ \)を用いて求めよ。ただし,変圧器二次側の送電線電流\( \ I_{\mathrm {s}} \ \mathrm {[A]} \ \),電線単位長抵抗\( \ r \ \mathrm {[\Omega / m ]} \ \)とし,配電線路の線路特性は均一として,電源電圧は一定であるものとする。
b) 図2に示すように,末端に行くほど直線的に減少する不平等負荷分布である単相\( \ 2 \ \)線式の低圧配電系統において,\( \ \mathrm {A}^{\prime } \ \)点から\( \ x^{\prime } \ \mathrm {[m]} \ \)だけ離れた地点の負荷電流密度\( \ i_{\mathrm {x}}^{\prime } \ \mathrm {[A / m]} \ \)及び線路電流\( \ I_{\mathrm {x}}^{\prime } \ \mathrm {[A]} \ \)を,\( \ \mathrm {A}^{\prime } \ \)点の負荷電流密度\( \ i_{0}^{\prime } \ \mathrm {[A / m]} \ \)を用いて求めたうえで,低圧配電線の全区間の電力損失を\( \ I_{\mathrm {s}} \ \),\( \ L \ \),\( \ r \ \)を用いて求めよ。ただし,電流分布以外の条件はa)と同様とする。
【ワンポイント解説】
電力損失に関する問題です。単相\( \ 2 \ \)線式というのが少し嫌らしい問題だなという印象があります。近年は本問のように論述問題と計算問題を組み合わせたような問題が1種2種ともに増えてきています。計算だけに偏らず総合的な能力を上げて行くことが重要となります。
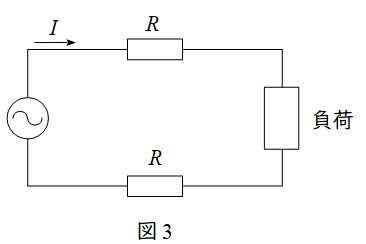
1.単相\( \ 2 \ \)線式系統の電力損失
単相\( \ 2 \ \)線式系統における電力損失\( \ P_{\mathrm {l}} \ \)は,線路の抵抗を\( \ R \ \),線路を流れる電流を\( \ I \ \)とすると,図3より,
\[
\begin{eqnarray}
P_{\mathrm {l}}&=&2RI^{2} \\[ 5pt ]
\end{eqnarray}
\]
となります。受電電力を\( \ P \ \),受電電圧を\( \ V_{\mathrm {r}} \ \),力率を\( \ \cos \theta \ \)とすると,
\[
\begin{eqnarray}
P&=&V_{\mathrm {r}}I\cos \theta \\[ 5pt ]
I&=&\frac {P}{V_{\mathrm {r}}\cos \theta } \\[ 5pt ]
\end{eqnarray}
\]
となるので,電力損失は,
\[
\begin{eqnarray}
P_{\mathrm {l}}&=&2RI^{2} \\[ 5pt ]
&=&2R\left( \frac {P}{V_{\mathrm {r}}\cos \theta }\right) ^{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められ,電圧を大きくする,力率を改善することで電力損失を低減することができることが分かります。
【解答】
(1)配電系統の電力損失低減策を三つ述べよ。
(ポイント)
・電力損失の低減≒電圧を大きくする,力率を改善する方法であり,その方策を検討する。
・単純に損失を低減する方法を考える。アモルファス変圧器の採用や電線の太線化等がある。
(試験センター解答)
以下の項目から\( \ 3 \ \)項目記載されていればよい。
・配電電圧を格上げする(昇圧)。
・力率改善用コンデンサを設置する。
・負荷電流の不平衡を是正する。
・電線の太線化
・回線数を増加する。(複線化,ネットワーク化,単相 3 線方式の採用など)
・低損失の柱上変圧器を適用
など
(2)a) 平等負荷分布における\( \ \mathrm {A} \ \)点から\( \ x \ \mathrm {[m]} \ \)だけ離れた地点の線路電流\( \ I_{\mathrm {x}} \ \mathrm {[A]} \ \)と低圧配電線の全区間の電力損失
図1において,単位長さ当たりの電流密度\( \ i_{\mathrm {x}} \ \)は,
\[
\begin{eqnarray}
i_{\mathrm {x}}&=&\frac {I_{\mathrm {s}}}{L} \\[ 5pt ]
\end{eqnarray}
\]
であるから,\( \ \mathrm {A} \ \)点から\( \ x \ \)だけ離れた地点の線路電流\( \ I_{\mathrm {x}} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {x}}&=&I_{\mathrm {s}}-i_{\mathrm {x}}x \\[ 5pt ]
&=&I_{\mathrm {s}}-\frac {I_{\mathrm {s}}}{L}\cdot x \\[ 5pt ]
&=&I_{\mathrm {s}}\cdot \frac {L-x}{L} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。微小区間\( \ \mathrm {d}x \ \)における電力損失\( \ \mathrm {d}P_{\mathrm {l}} \ \)は,微小区間の抵抗が\( \ r\mathrm {d}x \ \)であるので,
\[
\begin{eqnarray}
\mathrm {d}P_{\mathrm {l}}&=&2I_{\mathrm {x}}^{2}r\mathrm {d}x \\[ 5pt ]
&=&2\left( I_{\mathrm {s}}\cdot \frac {L-x}{L}\right) ^{2}r\mathrm {d}x \\[ 5pt ]
&=&\frac {2I_{\mathrm {s}}^{2}r}{L^{2}}\left( L-x\right) ^{2}\mathrm {d}x \\[ 5pt ]
&=&\frac {2I_{\mathrm {s}}^{2}r}{L^{2}}\left( x^{2}-2Lx +L^{2}\right) \mathrm {d}x \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,線路全体の電力損失\( \ P_{\mathrm {l}} \ \)は上式の両辺を積分すると,
\[
\begin{eqnarray}
P_{\mathrm {l}}&=&\int _{0}^{L}\frac {2I_{\mathrm {s}}^{2}r}{L^{2}}\left( x^{2}-2Lx +L^{2}\right) \mathrm {d}x \\[ 5pt ]
&=&\frac {2I_{\mathrm {s}}^{2}r}{L^{2}}\int _{0}^{L} \left( x^{2}-2Lx +L^{2} \right) \mathrm {d}x \\[ 5pt ]
&=&\frac {2I_{\mathrm {s}}^{2}r}{L^{2}}\left[ \frac {x^{3}}{3}-Lx^{2} +L^{2}x \right] _{0}^{L} \\[ 5pt ]
&=&\frac {2I_{\mathrm {s}}^{2}r}{L^{2}}\cdot \frac {L^{3}}{3} \\[ 5pt ]
&=&\frac {2I_{\mathrm {s}}^{2}Lr}{3} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)b) 不平等負荷分布における\( \ \mathrm {A}^{\prime } \ \)点から\( \ x^{\prime } \ \mathrm {[m]} \ \)だけ離れた地点の負荷電流密度\( \ i_{\mathrm {x}}^{\prime } \ \mathrm {[A / m]} \ \)及び線路電流\( \ I_{\mathrm {x}}^{\prime } \ \mathrm {[A]} \ \)と低圧配電線の全区間の電力損失
a)の線路電流\( \ I_{\mathrm {x}} \ \)の導出式と同様に,\( \ \mathrm {A}^{\prime } \ \)点から\( \ x^{\prime } \ \)離れた地点の負荷電流密度\( \ i_{\mathrm {x}}^{\prime } \ \)は,
\[
\begin{eqnarray}
i_{\mathrm {x}}^{\prime }&=&i_{\mathrm {0}}^{\prime }\cdot \frac {L-x^{\prime }}{L} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。\( \ x^{\prime } \ \)離れた地点の線路電流\( \ I_{\mathrm {x}}^{\prime } \ \)は,\( \ x^{\prime } \ \)から\( \ L \ \)までの負荷電流密度を合算したものであるから,
\[
\begin{eqnarray}
I_{\mathrm {x}}^{\prime }&=&\int _{x^{\prime }}^{L}i_{\mathrm {x}}^{\prime }\mathrm {d}x^{\prime } \\[ 5pt ]
&=&\int _{x^{\prime }}^{L}i_{\mathrm {0}}^{\prime }\cdot \frac {L-x^{\prime }}{L}\mathrm {d}x^{\prime } \\[ 5pt ]
&=&\frac {i_{\mathrm {0}}^{\prime }}{L}\int _{x^{\prime }}^{L}\left( L-x^{\prime }\right) \mathrm {d}x^{\prime } \\[ 5pt ]
&=&\frac {i_{\mathrm {0}}^{\prime }}{L}\left[ Lx^{\prime }-\frac {{x^{\prime }}^{2}}{2} \right] _{x^{\prime }}^{L} \\[ 5pt ]
&=&\frac {i_{\mathrm {0}}^{\prime }}{L}\left[ L^{2}-\frac {L^{2}}{2}-Lx^{\prime }+\frac {{x^{\prime }}^{2}}{2} \right] \\[ 5pt ]
&=&\frac {i_{\mathrm {0}}^{\prime }}{2L}\left[ L^{2}-2Lx^{\prime }+{x^{\prime }}^{2} \right] \\[ 5pt ]
&=&\frac {i_{\mathrm {0}}^{\prime }}{2L}\left( L-x^{\prime } \right) ^{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。よって,a)と同様に微小区間\( \ \mathrm {d}x^{\prime } \ \)における電力損失\( \ \mathrm {d}P_{\mathrm {l}}^{\prime } \ \)は,微小区間の抵抗が\( \ r\mathrm {d}x^{\prime } \ \)であるので,
\[
\begin{eqnarray}
\mathrm {d}P_{\mathrm {l}}^{\prime }&=&2{I_{\mathrm {x}}^{\prime }}^{2}r\mathrm {d}x^{\prime } \\[ 5pt ]
&=&2\left\{ \frac {i_{\mathrm {0}}^{\prime }}{2L}\left( L-x^{\prime } \right) ^{2}\right\} ^{2}r\mathrm {d}x^{\prime } \\[ 5pt ]
&=&\frac {{i_{\mathrm {0}}^{\prime }}^{2}r}{2L^{2}}\left( L-x^{\prime }\right) ^{4}\mathrm {d}x^{\prime } \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,線路全体の電力損失\( \ P_{\mathrm {l}}^{\prime } \ \)は上式の両辺を積分すると,
\[
\begin{eqnarray}
P_{\mathrm {l}}^{\prime }&=&\int _{0}^{L} \frac {{i_{\mathrm {0}}^{\prime }}^{2}r}{2L^{2}}\left( L-x^{\prime }\right) ^{4}\mathrm {d}x^{\prime } \\[ 5pt ]
&=&\frac {{i_{\mathrm {0}}^{\prime }}^{2}r}{2L^{2}}\int _{0}^{L} \left( L-x^{\prime }\right) ^{4}\mathrm {d}x^{\prime } \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,\( \ X=L-x^{\prime } \ \)とすれば\( \ x^{\prime } \ \)が\( \ 0 \ \)から\( \ L \ \)に変化するとき,\( \ X \ \)が\( \ L \ \)から\( \ 0 \ \)に変化し,\( \ \mathrm {d}X=-\mathrm {d}x^{\prime } \ \)であるので,
\[
\begin{eqnarray}
P_{\mathrm {l}}^{\prime }&=&\int _{0}^{L} \frac {{i_{\mathrm {0}}^{\prime }}^{2}r}{2L^{2}}\left( L-x^{\prime }\right) ^{4}\mathrm {d}x^{\prime } \\[ 5pt ]
&=&\frac {{i_{\mathrm {0}}^{\prime }}^{2}r}{2L^{2}}\int _{L}^{0} X ^{4}\cdot -\mathrm {d}X \\[ 5pt ]
&=&-\frac {{i_{\mathrm {0}}^{\prime }}^{2}r}{2L^{2}}\int _{L}^{0} X ^{4}\mathrm {d}X \\[ 5pt ]
&=&-\frac {{i_{\mathrm {0}}^{\prime }}^{2}r}{2L^{2}}\left[ \frac {X^{5}}{5}\right] _{L}^{0} \\[ 5pt ]
&=&-\frac {{i_{\mathrm {0}}^{\prime }}^{2}r}{2L^{2}}\left[ -\frac {L^{5}}{5}\right] \\[ 5pt ]
&=&\frac {{i_{\mathrm {0}}^{\prime }}^{2}L^{3}r}{10} \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,
\[
\begin{eqnarray}
I_{\mathrm {s}}&=&I_{\mathrm {x}}^{\prime }(0) \\[ 5pt ]
&=&\frac {i_{\mathrm {0}}^{\prime }L}{2} \\[ 5pt ]
\end{eqnarray}
\]
であるので,
\[
\begin{eqnarray}
P_{\mathrm {l}}^{\prime }&=&\frac {2{I_{\mathrm {s}}}^{2}Lr}{5} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは