《法規》〈電気施設管理〉[R07:問4]電力系統の周波数変動に関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，電力系統の周波数変動に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

$ \ \mathrm {a)} \ $電力系統の周波数は，電力系統の需要と供給のバランスで決まり，周波数変動（系統事故によるものや気象変化に伴う再生可能エネルギー電源の出力変動によるものを除く。）の原因となる負荷変動は，変動周期によって次の三つに大別することができる。

①　日間周期変化を持つもので，工場の始業・終業・昼休み，事務所・デパートなどの冷暖房，夕方からの照明器具の点灯などによって生じる負荷変動

②　数分～十数分程度の比較的短時間内の間に頻繁に起きるもので，圧延機，電気炉，その他一般負荷の不規則な負荷変動

③　予期しえない原因から生じる数分以下の偶発的短時間の負荷変動

これらによる周波数変動対策として，①の変動に対しては，中央給電指令所などで，前日までに託送供給契約者から提出された需要計画等を基に$ \ \fbox {　（１）　} \ $を作成し，発電契約者等から提出された発電計画等に基づいた各発電所の運転計画スケジュールにより対処する。②の負荷変動に対しては，主に周波数計を用いて周波数偏差$ \ \mathit {\Delta }f \ $を検出し，中央給電指令所の計算機システムにより変動分に応じた発電出力調整指令を送信することで，周波数の安定化制御を行う。③の変動に対しては，電力系統内の火力・水力発電所の発電機のうち，周波数の変化に応じて短時間の間に周波数が下がった場合に出力を上昇させ，周波数が上がった場合に出力を低下させる機能である$ \ \fbox {　（２）　} \ $運転機能をもつ発電機により，周波数調整を行う。

$ \ \mathrm {b)} \ $電力系統の需要と供給の不均衡が生ずると，これに応じ周波数も変化する。この需要・供給と周波数の変化の関係を電力系統の周波数特性と呼ぶ。需給不均衡量$ \ \mathit {\Delta } P \ \mathrm {[MW]} \ $（$ \ \mathit {\Delta } P \ $の符号は負荷の増加側，発電電力の減少側で正），周波数変化量$ \ \mathit {\Delta } f \ \mathrm {[Hz]} \ $であるとき，$ \ K ＝- \mathit {\Delta }P / \mathit {\Delta } f \ \mathrm {[MW / Hz]} \ $を系統周波数特性定数と呼び，$ \ \mathrm {[MW / 0.1Hz]} \ $若しくは総需要の百分率で表した$ \ \mathrm {[％MW / 0.1Hz]} \ $などの単位が用いられる。

例えば，負荷容量$ \ 10 \ 000 \ \mathrm {MW} \ $，系統周波数特性定数$ \ 1.0 \ \mathrm {[％MW / 0.1Hz]} \ $の系統で$ \ 100 \ \mathrm {MW} \ $の発電電力が減少したとき，周波数は$ \ \fbox {　（３）　} \ \mathrm {Hz} \ \fbox {　（４）　} \ $する。

$ \ \mathrm {c)} \ $電力系統の周波数変動に伴い，電圧や消費電力も変動する。周波数が上昇した場合，電動機では回転速度が上昇し，負荷の消費電力が増加する。周波数が低下した場合は，これらの逆の現象となり，結果的には周波数の変動を抑制しようとする作用がある。このような作用を負荷の$ \ \fbox {　（５）　} \ $という。

〔問4の解答群〕
\[
\begin{eqnarray}
&（イ）&　ガバナフリー　　　　　&（ロ）&　上昇 \\[ 5pt ] &（ハ）&　負荷周波数　　　　　&（ニ）&　自己制御性 \\[ 5pt ] &（ホ）&　経済負荷配分制御　　　　　　　　　&（ヘ）&　0.1 \\[ 5pt ] &（ト）&　自己安定性　　　　　&（チ）&　増加 \\[ 5pt ] &（リ）&　0.01　　　　　&（ヌ）&　低下 \\[ 5pt ] &（ル）&　予想日負荷曲線　　　　　&（ヲ）&　供給計画 \\[ 5pt ] &（ワ）&　自立制御性　　　　　&（カ）&　年間需給計画 \\[ 5pt ] &（ヨ）&　1.0 && \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

電力系統の周波数変動に関する出題です。
近年出題が少ない問題でしたが，電力管理科目の令和5年問6で類題が出題されたため，二次試験に向けて過去問学習をされていた方が有利な問題であったかなと思います。

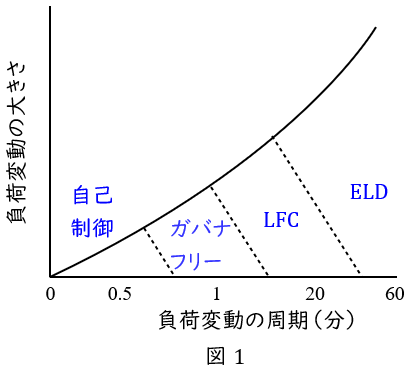
1.電力系統における周波数調整方法
①微小変動(数秒～数十秒の変動)
負荷の自己制御性を利用して調整します。一般的な回転機負荷は周波数が上がると消費電力が増え，周波数が下がると消費電力が減少します。この特性を利用し周波数を制御します。

②短周期変動(数秒～数分程度の変動)
発電系統のガバナフリー運転で調整します。発電機の調速機によって周波数変化量から出力変化量を約$ \ 1.0 \ \mathrm {[％MW／0.1Hz]} \ $程度で調整します。例えば火力発電所であったら，タービン入口のガバナ開度を周波数が低い場合は増加し，周波数が高い場合は減少させて蒸気流入量を調整します。

③長周期変動(数分～数十分の変動)
系統の周波数と基準周波数の偏差を検出して中央給電指令所からの制御信号に伴い，負荷周波数制御$ \ \left( \mathrm {LFC}\right) \ $で調整します。火力発電所であれば，中央給電指令所からの信号に合わせ出力をコントロールさせます。

④日負荷変動(数十分～数時間の変動)
天候，気温，湿度等のデータを元に需要予測を決定し，出力配分を各発電所の信号へ送ります。経済負荷配分制御$ \ \left( \mathrm {ELD}\right) \ $により最も経済的な配分を行い，各発電機の出力調整，起動停止等を行います。

2.系統周波数特性係数
一般に$ \ K \ \mathrm {[MW / Hz]} \ $もしくは$ \ K^{\prime } \ \mathrm {[MW / 0.1Hz]} \ $で表され，電源の容量が変化した際に系統周波数がどれだけ変化するかを示す指標となります。定量的に示すと，電源が$ \ \Delta P \ \mathrm {[MW]} \ $変化したときの系統周波数の変化$ \ \Delta f \ \mathrm {[Hz]} \ $は，
\[
\begin{eqnarray}
\Delta f &=&\frac {\Delta P}{K} \\[ 5pt ] &=&\frac {\Delta P}{10K^{\prime }} \\[ 5pt ] \end{eqnarray}
\] となります。

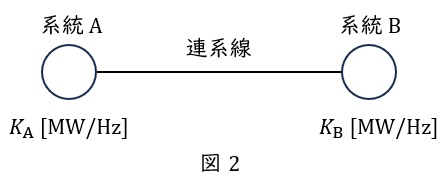
また，図2のように$ \ 2 \ $系統以上の系統周波数特性係数が与えられている場合について，系統周波数特性係数$ \ K_{\mathrm {A}} \ \mathrm {[MW / Hz]} \ $の系統$ \ \mathrm {A} \ $と系統周波数特性係数$ \ K_{\mathrm {B}} \ \mathrm {[MW / Hz]} \ $の系統$ \ \mathrm {B} \ $があった場合，全体の系統周波数特性係数$ \ K \ \mathrm {[MW / Hz]} \ $は，
\[
\begin{eqnarray}
K&=&K_{\mathrm {A}}+K_{\mathrm {B}} \\[ 5pt ] \end{eqnarray}
\] となり，例えば，系統$ \ \mathrm {A} \ $で$ \ \Delta P_{\mathrm {A}} \ \mathrm {[MW]} \ $変化があったときの系統全体の周波数変化量$ \ \Delta f \ \mathrm {[Hz]} \ $は，
\[
\begin{eqnarray}
\Delta f &=&\frac {\Delta P_{\mathrm {A}}}{K} \\[ 5pt ] &=&\frac {\Delta P_{\mathrm {A}}}{K_{\mathrm {A}}+K_{\mathrm {B}}} \\[ 5pt ] \end{eqnarray}
\] であり，このときの連系線$ \ \mathrm {A-B} \ $の潮流変化$ \ \Delta P_{\mathrm {T}} \ \mathrm {[MW]} \ $は，
\[
\begin{eqnarray}
\Delta P_{\mathrm {T}} &=&\Delta f K_{\mathrm {B}} \\[ 5pt ] &=&\frac {K_{\mathrm {B}} }{K_{\mathrm {A}}+K_{\mathrm {B}}}\Delta P_{\mathrm {A}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：ル
題意より解答候補は，（ル）予想日負荷曲線，（ヲ）供給計画，（カ）年間需給計画，になると思います。
ワンポイント解説「1.電力系統における周波数調整方法」の通り，日間周期変化に対しては，託送供給契約者から提出された需要計画等を基に需要予測を決定します。一日の需要予測の変化を表す線を予想日負荷曲線といいます。供給計画というと，年単位等の長期的な供給計画を指すのが一般的です。

(2)解答：イ
題意より解答候補は，（イ）ガバナフリー，（ホ）経済負荷配分制御，等になると思います。
ワンポイント解説「1.電力系統における周波数調整方法」の通り，電力系統内の火力・水力発電所の発電機のうち，周波数の変化に応じて短時間の間に周波数が下がった場合に出力を上昇させ，周波数が上がった場合に出力を低下させる機能をガバナフリーといいます。

(3)解答：ヘ
負荷容量$ \ 10 \ 000 \ \mathrm {MW} \ $，系統周波数特性定数$ \ 1.0 \ \mathrm {[％MW / 0.1Hz]} \ $なので，$ \ \mathrm {MW} \ $に換算した系統周波数特性定数$ \ K \ \mathrm {[MW / Hz]} \ $は，
\[
\begin{eqnarray}
K&=&10 \ 000\times \frac {1.0}{100} \times 10 \\[ 5pt ] &=&1 \ 000 \ \mathrm {[MW / Hz]} \\[ 5pt ] \end{eqnarray}
\] となるので，$ \ \mathit {\Delta } P=100 \ \mathrm {[MW]} \ $の発電電力が減少したときの周波数変化量$ \ \mathit {\Delta }f \ \mathrm {[Hz]} \ $は，ワンポイント解説「2.系統周波数特性係数」の通り，
\[
\begin{eqnarray}
\Delta f &=&\frac {100}{1 \ 000} \\[ 5pt ] &=&0.1 \ \mathrm {[Hz]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ヌ
題意より解答候補は，（ロ）上昇，（チ）増加，（ヌ）低下，になると思います。
発電電力が減少した際は$ \ \mathit {\Delta } P \ $の符号は正となり，$ \ K ＝- \mathit {\Delta }P / \mathit {\Delta } f \ $より$ \ \mathit {\Delta } f \ $は負となるので，周波数は低下することになります。概念として「発電電力が低下する→駆動力が弱くなる→回転速度が遅くなる→周波数が低下する」というイメージを持つとわかりやすいかと思います。

(5)解答：ニ
題意より解答候補は，（ニ）自己制御性，（ト）自己安定性，（ワ）自立制御性，になると思います。
ワンポイント解説「1.電力系統における周波数調整方法」の通り，負荷の特性により周波数の変動を抑制しようとする作用を自己制御性といいます。