Contents
【問題】
【難易度】★★★☆☆(普通)
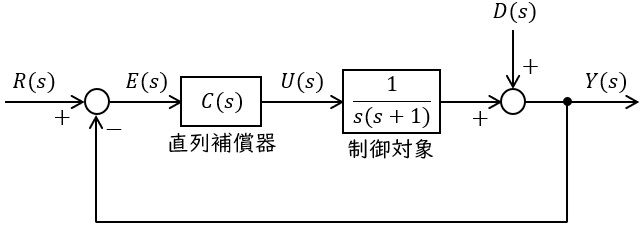
図のようなフィードバック制御系について,次の問に答えよ。ただし,\( \ R \left( s \right) \ \)は目標値,\( \ D \left( s \right) \ \)は外乱,\( \ Y \left( s \right) \ \)は制御量,\( \ E \left( s \right) \ \)は偏差とする。また,数値で答える場合には,小数点以下\( \ 3 \ \)けた目を四捨五入した\( \ 2 \ \)けたとする。
(1) \( \ R(s) = 0 \ \),\( \ C(s) = K \ \)のとき,外乱\( \ D \left( s \right) \ \)の時間関数がランプ関数\( \ d \left( t \right) =2t \ \)で与えられる場合の定常速度偏差を求めよ。
(2) \( \ C(s) = K \ \)のとき,閉ループ系の安定性の指標の一つである減衰定数\( \ \zeta \ \)を\( \ 0.8 \ \)に設定するための\( \ K \ \)の値を求めよ。
(3) \( \ \displaystyle C(s)=A\cdot \frac {s+1}{0.1s+1} \ \)の場合について,\( \ R \left( s \right) \ \)から\( \ Y \left( s \right) \ \)までの閉ループ伝達関数を求めよ。
(4) 上記(3)を\( \ C \left( s \right) \ \)を用いた閉ループ系の減衰定数\( \ \zeta \ \)が\( \ 0.8 \ \)になるような\( \ A \ \)の値を求めよ。このとき,上記(2)の場合と比較して閉ループ系の固有角周波数を求めることにより速応性はどのくらい変化したかを説明せよ。
【ワンポイント解説】
フィードバック制御系の伝達関数の導出及び減衰係数と固有角周波数に関する問題です。
いずれも\( \ 2 \ \)種二次試験の自動制御では重要となる内容ばかりですので,各設問を解けるようにしておきましょう。
(2)以降「外乱\( \ D \left( s \right) =0 \ \)とする。」という条件が抜けているのが気になりますが,設計上の考えなので外乱は考えないという意味かもしれません。
1.基本的なラプラス変換
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると以下のような関係があります。
\[
\begin{array}{|c|c|}
\hline
f(t) & F(s) \\
\hline
{\displaystyle \delta (t) }\atop{単位インパルス関数} & 1 \\[ 5pt ]
{\displaystyle u (t) }\atop{単位ステップ関数} & \displaystyle \frac {1}{s} \\[ 5pt ]
K & \displaystyle \frac {K}{s} \\[ 5pt ]
t & \displaystyle \frac {1}{s^{2}} \\[ 5pt ]
\mathrm {e}^{at} & \displaystyle \frac {1}{s-a} \\[ 5pt ]
\sin \omega t & \displaystyle \frac {\omega }{s^{2}+\omega ^{2}} \\[ 5pt ]
\cos \omega t & \displaystyle \frac {s}{s^{2}+\omega ^{2}} \\[ 5pt ]
\displaystyle \frac {\mathrm {d}f\left( t \right) }{\mathrm {d}t} & sF\left( s \right) -f\left( 0 \right) \\[ 5pt ]
\displaystyle \int f\left( t \right) \mathrm {d}t & \displaystyle \frac {F\left( s \right) }{s}+\frac {1}{s}\int _{-\infty }^{0}f\left( \tau \right) \mathrm {d}\tau \\[ 5pt ]
\hline
\end{array}
\]
2.ブロック線図の考え方
①直列
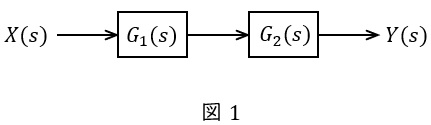
図1のような伝達関数\( \ G_{1}(s) \ \),\( \ G_{2}(s) \ \)が与えられているとき,全体の伝達関数\( \ G(s) \ \)は,
\[
\begin{eqnarray}
G(s)&=&\frac {Y(s)}{X(s)}=G_{1}(s)G_{2}(s) \\[ 5pt ]
\end{eqnarray}
\]
となります。
②並列
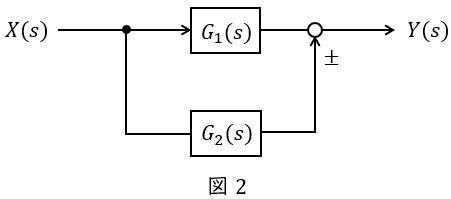
図2のような伝達関数\( \ G_{1}(s) \ \),\( \ G_{2}(s) \ \)が与えられているとき,全体の伝達関数\( \ G(s) \ \)は,
\[
\begin{eqnarray}
G(s)&=&\frac {Y(s)}{X(s)}=G_{1}(s)±G_{2}(s) \\[ 5pt ]
\end{eqnarray}
\]
となります。
③フィードバック
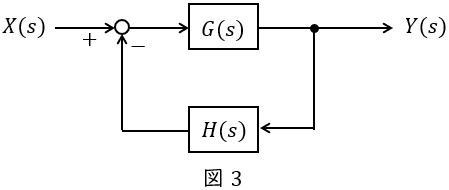
図3のような\( \ G(s) \ \),\( \ H(s) \ \)が与えられているとき,全体の伝達関数\( \ W(s) \ \)は,
\[
\begin{eqnarray}
Y(s)&=&\left\{ X(s) -H(s)Y(s) \right\} G(s) \\[ 5pt ]
Y(s)&=&G(s)X(s) -G(s)H(s)Y(s) \\[ 5pt ]
Y(s)+G(s)H(s)Y(s) &=&G(s)X(s) \\[ 5pt ]
\left\{ 1+G(s)H(s)\right\} Y(s) &=&G(s)X(s) \\[ 5pt ]
\frac {Y(s)}{X(s)}&=&\frac {G(s)}{1+G(s)H(s)} \\[ 5pt ]
W(s)&=&\frac {G(s)}{1+G(s)H(s)} \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.減衰係数\( \ \zeta \ \)と固有角周波数\( \ \omega _{\mathrm {n}} \ \)
\( \ 2 \ \)次遅れの伝達関数\( \ W(s) \ \)の一般式は,減衰係数\( \ \zeta \ \),固有角周波数\( \ \omega _{\mathrm {n}} \ \mathrm {[rad / s]} \ \)とすると,
\[
\begin{eqnarray}
W(s)&=&\frac {\omega _{\mathrm {n}}^{2}}{s^{2}+2\zeta \omega _{\mathrm {n}}s+\omega _{\mathrm {n}}^{2}} \\[ 5pt ]
\end{eqnarray}
\]
で表されます。
4.最終値の定理
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると,\( \ f(t) \ \)の定常値は,
\[
\begin{eqnarray}
\displaystyle \lim _{ t \to \infty } f(t)&=&\displaystyle \lim _{ s \to 0 } sF(s) \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
【解答】
(1)\( \ R(s) = 0 \ \),\( \ C(s) = K \ \)のとき,\( \ D \left( s \right) \ \)の時間関数が\( \ d \left( t \right) =2t \ \)で与えられる場合の定常速度偏差
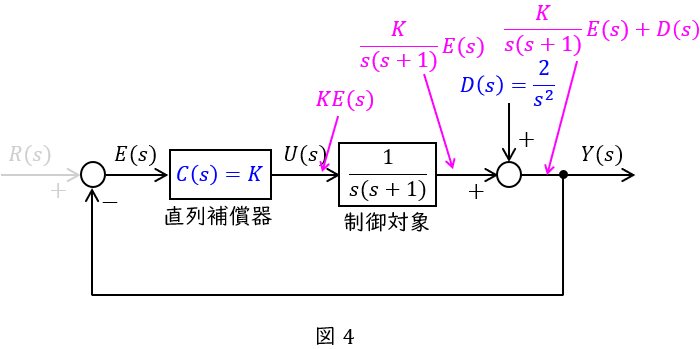
\( \ d \left( t \right) =2t \ \)のラプラス変換は\( \ \displaystyle D \left( s \right) = \frac {2}{s^{2}} \ \)となり,図4に示すように,
\[
\begin{eqnarray}
U \left( s \right) &=&C \left( s \right) E \left( s \right) \\[ 5pt ]
&=&KE \left( s \right) \\[ 5pt ]
Y \left( s \right) &=&\frac {1}{s\left( s+1 \right) }U \left( s \right) +D \left( s \right) \\[ 5pt ]
&=&\frac {K}{s\left( s+1 \right) }E \left( s \right) +D \left( s \right) \\[ 5pt ]
E \left( s \right) &=&-Y \left( s \right) \\[ 5pt ]
&=&-\frac {K}{s\left( s+1 \right) }E \left( s \right) -D \left( s \right) \\[ 5pt ]
\end{eqnarray}
\]
の関係があるので,これを整理すると,
\[
\begin{eqnarray}
E \left( s \right) +\frac {K}{s\left( s+1 \right) }E \left( s \right) &=& -D \left( s \right) \\[ 5pt ]
\left\{ 1 +\frac {K}{s\left( s+1 \right) } \right\} E \left( s \right) &=& -D \left( s \right) \\[ 5pt ]
\left\{ \frac {s\left( s+1 \right) +K}{s\left( s+1 \right) } \right\} E \left( s \right) &=&-\frac {2}{s^{2}} \\[ 5pt ]
E \left( s \right) &=&-\frac {s\left( s+1 \right) }{s\left( s+1 \right) +K} \cdot \frac {2}{s^{2}} \\[ 5pt ]
&=&-\frac {s+1 }{s\left( s+1 \right) +K} \cdot \frac {2}{s} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,定常速度偏差は,ワンポイント解説「4.最終値の定理」の通り,
\[
\begin{eqnarray}
\displaystyle \lim _{ t \to \infty } e(t)&=&\displaystyle \lim _{ s \to 0 } sE(s) \\[ 5pt ]
&=&\displaystyle \lim _{ s \to 0 } \left[ s\cdot \left\{ – \frac {s+1 }{s\left( s+1 \right) +K}\right\} \cdot \frac {2}{s} \right] \\[ 5pt ]
&=&\displaystyle \lim _{ s \to 0 } \left\{ – \frac {s+1 }{s\left( s+1 \right) +K} \cdot 2 \right\} \\[ 5pt ]
&=&-\frac {0+1 }{0\times \left( 0+1 \right) +K} \times 2 \\[ 5pt ]
&=&-\frac {2}{K} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)\( \ C(s) = K \ \)のとき,\( \ \zeta \ \)を\( \ 0.8 \ \)に設定するための\( \ K \ \)
\( \ R \left( s \right) \ \)から\( \ Y \left( s \right) \ \)までの伝達関数\( \ W \left( s \right) \ \)は,ワンポイント解説「2.ブロック線図の考え方」の通り,
\[
\begin{eqnarray}
W \left( s \right) &=&\frac {\displaystyle \frac {C \left( s \right) }{s\left( s+1\right) }}{\displaystyle 1+\frac {C \left( s \right) }{s\left( s+1\right) }} \\[ 5pt ]
&=&\frac {\displaystyle \frac {C \left( s \right) }{s\left( s+1\right) }}{\displaystyle \frac {s\left( s+1\right) +C \left( s \right) }{s\left( s+1\right) }} \\[ 5pt ]
&=&\frac {C \left( s \right) }{s\left( s+1\right) +C \left( s \right) } \\[ 5pt ]
&=&\frac {K }{s^{2}+s+K } \\[ 5pt ]
\end{eqnarray}
\]
であり,ワンポイント解説「3.減衰係数\( \ \zeta \ \)と固有角周波数\( \ \omega _{\mathrm {n}} \ \)」の通り,
\[
\begin{eqnarray}
{\omega _{n}}^{2} &=&K ⇔ \omega _{n}=\sqrt {K} \\[ 5pt ]
2\zeta \omega _{n} &=&1 \\[ 5pt ]
2\times 0.8\times \sqrt {K} &=&1 \\[ 5pt ]
\sqrt {K}&=&0.625 \\[ 5pt ]
K&≒&0.390 \ 63 → 0.39 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ \displaystyle C(s)=A\cdot \frac {s+1}{0.1s+1} \ \)の場合の\( \ R \left( s \right) \ \)から\( \ Y \left( s \right) \ \)までの閉ループ伝達関数
(2)と同様に,\( \ R \left( s \right) \ \)から\( \ Y \left( s \right) \ \)までの閉ループ伝達関数\( \ W \left( s \right) \ \)は,
\[
\begin{eqnarray}
W \left( s \right) &=&\frac {C \left( s \right) }{s\left( s+1\right) +C \left( s \right) } \\[ 5pt ]
&=&\frac {\displaystyle A\cdot \frac {s+1}{0.1s+1} }{\displaystyle s\left( s+1\right) +A\cdot \frac {s+1}{0.1s+1}} \\[ 5pt ]
&=&\frac {\displaystyle \frac {A\left( s+1\right) }{0.1s+1} }{\displaystyle \frac {s\left( s+1\right) \left( 0.1s+1\right) +A\left( s+1\right) }{0.1s+1}} \\[ 5pt ]
&=&\frac {A\left( s+1\right) }{s\left( s+1\right) \left( 0.1s+1\right) +A\left( s+1\right) } \\[ 5pt ]
&=&\frac {A }{s \left( 0.1s+1\right) +A } \\[ 5pt ]
&=&\frac {10A }{s \left( s+10\right) +10A } \\[ 5pt ]
&=&\frac {10A}{s^{2}+10s +10A} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)\( \ \zeta \ \)が\( \ 0.8 \ \)になるような\( \ A \ \)と速応性の変化
(3)解答式において,ワンポイント解説「3.減衰係数\( \ \zeta \ \)と固有角周波数\( \ \omega _{\mathrm {n}} \ \)」より,
\[
\begin{eqnarray}
{\omega _{n}}^{2} &=&10A ⇔ \omega _{n}=\sqrt {10A} \\[ 5pt ]
2\zeta \omega _{n} &=&10 \\[ 5pt ]
2\times 0.8\times \sqrt {10A} &=&10 \\[ 5pt ]
\sqrt {10A}&=&6.25 \\[ 5pt ]
10A&≒&39.063 \\[ 5pt ]
A&≒&3.906 → 3.91 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。このとき,固有角周波数\( \ \omega _{n} \ \mathrm {[rad / s]} \ \)は,
\[
\begin{eqnarray}
\omega _{n} &=&\sqrt {10A} \\[ 5pt ]
&=&6.25 \ \mathrm {[rad / s]} \\[ 5pt ]
\end{eqnarray}
\]
であり,(2)のときの固有角周波数\( \ \omega _{n} \ \mathrm {[rad / s]} \ \)は,
\[
\begin{eqnarray}
\omega _{n} &=&\sqrt {K} \\[ 5pt ]
&=&0.625 \ \mathrm {[rad / s]} \\[ 5pt ]
\end{eqnarray}
\]
であるため,同じ減衰定数に対し,速応性は\( \ 10 \ \)倍改善されていることになる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは