《機械・制御》〈パワーエレクトロニクス〉[H23:問3]チョッパを利用した二次電池の充放電に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

図1に示すチョッパを使用して，二次電池を充放電することを考える。直流電源電圧\( \ E_{\mathrm {p}} \ \)は二次電池電圧\( \ E_{\mathrm {b}} \ \)に比べて十分高く，チョッパは安定に動作し，\( \ L \ \)のインダクタンスは十分大きく\( \ I_{\mathrm {2}} \ \)は一定とする。電池\( \ \mathrm {SB} \ \)は充放電のヒステリシス特性などがなく，図2に示すその等価回路は一定の内部抵抗\( \ R_{\mathrm {i}} \ \)と電圧源\( \ E_{\mathrm {i}} \ \)との直列回路で表すことができるものとする。また，この電圧源\( \ E_{\mathrm {i}} \ \)は，電池容量\( \ \left( \mathrm {Ah}\right) \ \)に対応する\( \ 0 \ \mathrm {[％]} \ \)から\( \ 100 \ \mathrm {[％]} \ \)までの充電量\( \ \mathrm {SOC} \ \)と電圧\( \ e_{\mathrm {i}} \ \)が直線関係となる理想的な特性であるものとする。次の問に答えよ。

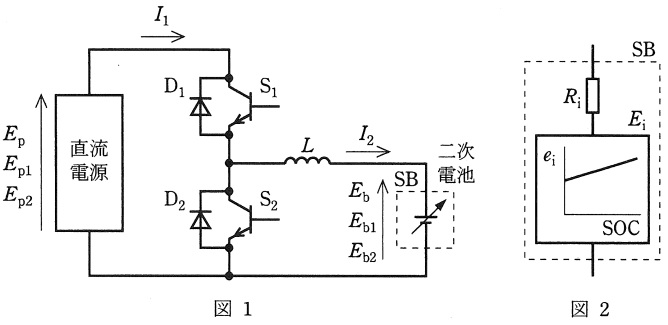
(1)　二次電池の充電はトランジスタ\( \ \mathrm {S_{1}} \ \)又は\( \ \mathrm {S_{2}} \ \)の一方だけをオン，オフ制御して行う。このとき電流が流れるのはトランジスタ\( \ \mathrm {S_{1}} \ \)，\( \ \mathrm {S_{2}} \ \)，ダイオード\( \ \mathrm {D_{1}} \ \)，\( \ \mathrm {D_{2}} \ \)のうちでどれか。

また，このときオン，オフ制御するトランジスタのオン時間を\( \ T_{\mathrm {on}} \ \)，オフ時間を\( \ T_{\mathrm {off}} \ \)，直流電源電圧を\( \ E_{\mathrm {p1}} \ \)，二次電池電圧を\( \ E_{\mathrm {b1}} \ \)とすると，\( \ E_{\mathrm {p1}} \ \)と\( \ E_{\mathrm {b1}} \ \)との関係はどのような式で表されるか。

(2)　二次電池を放電して直流電源が負荷となる動作をするときもトランジスタ\( \ \mathrm {S_{1}} \ \)又は\( \ \mathrm {S_{2}} \ \)の一方だけをオン，オフ制御する。このとき電流が流れるのはトランジスタ\( \ \mathrm {S_{1}} \ \)，\( \ \mathrm {S_{2}} \ \)，ダイオード\( \ \mathrm {D_{1}} \ \)，\( \ \mathrm {D_{2}} \ \)のうちでどれか。

また，このときオン，オフ制御するトランジスタのオン時間を\( \ T_{\mathrm {on}} \ \)，オフ時間を\( \ T_{\mathrm {off}} \ \)，直流電源電圧を\( \ E_{\mathrm {p2}} \ \)，二次電池電圧を\( \ E_{\mathrm {b2}} \ \)とすると，\( \ E_{\mathrm {p2}} \ \)と\( \ E_{\mathrm {b2}} \ \)との関係はどのような式で表されるか。

(3)　\( \ \mathrm {C} \ \)レートは電池の全容量を充放電しきる速度を表し，例えば\( \ \mathrm {3C} \ \)放電とは，「全容量を放電するのに\( \ \mathrm {1} \ \)時間かかる一定電流に対して，\( \ \mathrm {3} \ \)倍の電流を流して放電する」という意味である。図3には時刻\( \ t_{\mathrm {0}} \ \)で\( \ \mathrm {SOC} \ \)\( \ 0 \ \mathrm {[％]} \ \)から\( \ \mathrm {1C} \ \)で充電を始めて時刻\( \ t_{\mathrm {1}} \ \)で電池容量\( \ \left( \mathrm {Ah}\right) \ \)の充電が完了し，同時に\( \ \mathrm {2C} \ \)で放電を始めて時刻\( \ t_{\mathrm {2}} \ \)でその電池容量\( \ \left( \mathrm {Ah}\right) \ \)の放電を完了する運転パターンを示している。二次電池は容量\( \ 10 \ \mathrm {[A\cdot h]} \ \)で，内部抵抗が\( \ R_{\mathrm {i}}=0.005 \ \mathrm {[\Omega ]} \ \)であったとする。このときに，図3と同じ図が答案用紙に印刷されているので，二次電池電圧\( \ E_{\mathrm {b}} \ \)及び二次電池電流\( \ I_{\mathrm {2}} \ \)が時刻\( \ t_{\mathrm {0}} \ \)から時刻\( \ t_{\mathrm {2}} \ \)までどのような値になって変化するかを図中に太線で明確に描け。また，図示する充電時間\( \ T_{\mathrm {c}} \ \mathrm {[h]} \ \)及び放電時間\( \ T_{\mathrm {d}} \ \mathrm {[h]} \ \)はいくらか。

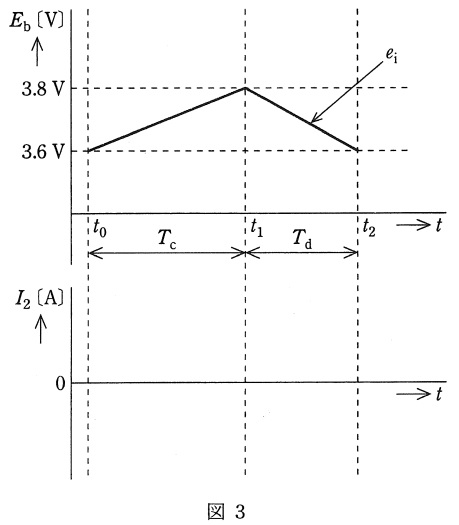
(4)　二次電池を充電する方法には，一般に定電流充電と定電圧充電とがある。放電が進んで電圧が低くなった二次電池を，通常使用されている端子電圧以内で充電する電力量に対して，内部抵抗による損失が少ないすなわちエネルギー効率のよい充電方法はいずれか。

【ワンポイント解説】

前半が可逆チョッパのメカニズム，後半が\( \ \mathrm {C} \ \)レートに関する問題となっています。
機械制御科目の中では計算量が比較的少ない問題なので，知識をしっかりと持っている場合には選択すると良い問題となります。

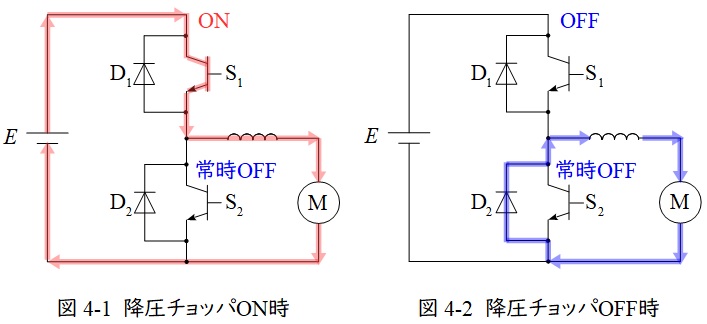
1.可逆チョッパ
降圧チョッパと昇圧チョッパを組み合わせたようなチョッパで，電源電圧と異なる負荷に電力を供給することと負荷の制動トルクを電源に回生することの両方が可能となります。
①降圧チョッパとして動作する時
図4-1及び図4-2のように動作します。
スイッチ\( \ \mathrm {S_{2}} \ \)は常時\( \ \mathrm {OFF} \ \)でスイッチ\( \ \mathrm {S_{1}} \ \)で\( \ \mathrm {ON－OFF} \ \)制御します。
\( \ \mathrm {S_{1}} \ \)が\( \ \mathrm {ON} \ \)の時，図4-1のように電源－\( \ \mathrm {S_{1}} \ \)－リアクトル－負荷－電源と導通し，リアクトルと負荷に電力が供給されます。
\( \ \mathrm {S_{1}} \ \)が\( \ \mathrm {OFF} \ \)の時，図4-2のようにリアクトル－負荷－ダイオード－リアクトルと導通し，リアクトルに蓄えられているエネルギーが放出されます。
全体としてリアクトルに蓄えられるエネルギーと放出されるエネルギーの量が等しいので，負荷電圧を\( \ V \ \)とすると，
\[
\begin{eqnarray}
\left( E-V\right)IT_{\mathrm {on}} &=&VIT_{\mathrm {off}} \\[ 5pt ] \left( E-V\right)T_{\mathrm {on}} &=&VT_{\mathrm {off}} \\[ 5pt ] ET_{\mathrm {on}} &=&V\left( T_{\mathrm {on}}+T_{\mathrm {off}}\right) \\[ 5pt ] V &=&\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}E \\[ 5pt ] &=&\alpha E \\[ 5pt ] \end{eqnarray}
\] となり，\( \ \displaystyle \alpha =\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}} \ \)を通流率といいます。\( \ \alpha ＜1 \ \)なので，\( \ E＞V \ \)となります。

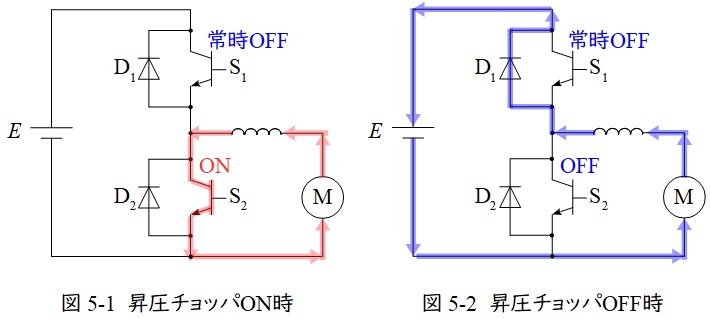
②昇圧チョッパとして動作する時
図5-1及び図5-2のように動作します。
スイッチ\( \ \mathrm {S_{1}} \ \)は常時\( \ \mathrm {OFF} \ \)でスイッチ\( \ \mathrm {S_{2}} \ \)で\( \ \mathrm {ON－OFF} \ \)制御します。
\( \ \mathrm {S_{2}} \ \)が\( \ \mathrm {ON} \ \)の時，図5-1のように負荷－リアクトル－\( \ \mathrm {S_{2}} \ \)－負荷と導通し，負荷からの回生エネルギーがリアクトルに蓄えられます。
\( \ \mathrm {S_{2}} \ \)が\( \ \mathrm {OFF} \ \)の時，図5-2のようにリアクトル－ダイオード－電源－負荷－リアクトルと導通し，リアクトルに蓄えられているエネルギーが放出され，電源に回生されます。
全体としてリアクトルに蓄えられるエネルギーと放出されるエネルギーの量が等しいので，負荷電圧を\( \ V \ \)とすると，
\[
\begin{eqnarray}
VIT_{\mathrm {on}} &=&\left( E-V\right) IT_{\mathrm {off}} \\[ 5pt ] VT_{\mathrm {on}} &=&\left( E-V\right) T_{\mathrm {off}} \\[ 5pt ] V\left( T_{\mathrm {on}}+T_{\mathrm {off}}\right) &=&ET_{\mathrm {off}} \\[ 5pt ] E &=&\frac {T_{\mathrm {on}}+T_{\mathrm {off}}}{T_{\mathrm {off}}}V \\[ 5pt ] \end{eqnarray}
\] となります。上式を通流率\( \ \alpha \ \)を用いて表すと，
\[
\begin{eqnarray}
\alpha &=&\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}} \\[ 5pt ] \left( T_{\mathrm {on}}+T_{\mathrm {off}}\right) \alpha &=&T_{\mathrm {on}} \\[ 5pt ] \alpha T_{\mathrm {off}}&=&\left( 1-\alpha \right) T_{\mathrm {on}} \\[ 5pt ] T_{\mathrm {on}}&=&\frac {\alpha }{1-\alpha }T_{\mathrm {off}} \\[ 5pt ] \end{eqnarray}
\] であるから，
\[
\begin{eqnarray}
E &=&\frac {T_{\mathrm {on}}+T_{\mathrm {off}}}{T_{\mathrm {off}}}V \\[ 5pt ] &=&\left( 1+\frac {T_{\mathrm {on}}}{T_{\mathrm {off}}}\right) V \\[ 5pt ] &=&\left( 1+\frac {\displaystyle \frac {\alpha }{1-\alpha }T_{\mathrm {off}}}{T_{\mathrm {off}}}\right) V \\[ 5pt ] &=&\left( 1+\frac {\alpha }{1-\alpha }\right) V \\[ 5pt ] &=&\frac {1}{1-\alpha } V \\[ 5pt ] \end{eqnarray}
\] となり，\( \ V＜E \ \)となります。

【解答】

(1)充電時に電流が流れる素子及び直流電源電圧と二次電池電圧の関係
ワンポイント解説「1.可逆チョッパ」図4-1，図4-2の通り，充電時は図1の\( \ \mathrm {S_{1}} \ \)がオン，オフ制御することで二次電池を充電させる。また，\( \ \mathrm {S_{1}} \ \)がオフのときに電流が流れるのは\( \ \mathrm {D_{2}} \ \)である。
ワンポイント解説「1.可逆チョッパ　①降圧チョッパとして動作する時」の通り，\( \ E_{\mathrm {p1}} \ \)と\( \ E_{\mathrm {b1}} \ \)の関係は，
\[
\begin{eqnarray}
E_{\mathrm {b1}} &=&\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}E_{\mathrm {p1}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)放電時に電流が流れる素子及び直流電源電圧と二次電池電圧の関係
ワンポイント解説「1.可逆チョッパ」図5-1，図5-2の通り，放電時は図1の\( \ \mathrm {S_{2}} \ \)がオン，オフ制御することで二次電池を放電させる。また，\( \ \mathrm {S_{2}} \ \)がオフのときに電流が流れるのは\( \ \mathrm {D_{1}} \ \)である。
ワンポイント解説「1.可逆チョッパ　②昇圧チョッパとして動作する時」の通り，\( \ E_{\mathrm {p2}} \ \)と\( \ E_{\mathrm {b2}} \ \)の関係は，
\[
\begin{eqnarray}
E_{\mathrm {p2}} &=&\frac {T_{\mathrm {on}}+T_{\mathrm {off}}}{T_{\mathrm {off}}}E_{\mathrm {b2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)二次電池電圧\( \ E_{\mathrm {b}} \ \)及び二次電池電流\( \ I_{\mathrm {2}} \ \)が時刻\( \ t_{\mathrm {0}} \ \)から時刻\( \ t_{\mathrm {2}} \ \)までどのような値になって変化するか。充電時間\( \ T_{\mathrm {c}} \ \mathrm {[h]} \ \)及び放電時間\( \ T_{\mathrm {d}} \ \mathrm {[h]} \ \)はいくらか。
二次電池の容量が\( \ 10 \ \mathrm {[A\cdot h]} \ \)であるから，\( \ \mathrm {1C} \ \)で充電するときの\( \ I_{\mathrm {2}} \ \)の大きさは，
\[
\begin{eqnarray}
I_{\mathrm {2}} &=&\frac {10}{1} \\[ 5pt ] &=&10 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるので，このときの二次電池電圧\( \ E_{\mathrm {b}} \ \)と\( \ E_{\mathrm {i}} \ \)の関係は，
\[
\begin{eqnarray}
E_{\mathrm {b}} &=&E_{\mathrm {i}}+R_{\mathrm {i}}I_{\mathrm {2}} \\[ 5pt ] &=&E_{\mathrm {i}}+0.005\times 10 \\[ 5pt ] &=&E_{\mathrm {i}}+0.05 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。また，\( \ \mathrm {2C} \ \)で放電するときの\( \ I_{\mathrm {2}} \ \)の大きさは，
\[
\begin{eqnarray}
I_{\mathrm {2}} &=&\frac {10}{0.5} \\[ 5pt ] &=&20 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるので，このときの二次電池電圧\( \ E_{\mathrm {b}} \ \)と\( \ E_{\mathrm {i}} \ \)の関係は，
\[
\begin{eqnarray}
E_{\mathrm {b}} &=&E_{\mathrm {i}}-R_{\mathrm {i}}I_{\mathrm {2}} \\[ 5pt ] &=&E_{\mathrm {i}}-0.005\times 20 \\[ 5pt ] &=&E_{\mathrm {i}}-0.1 \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] となる。以上から，それぞれの電圧及び電流波形は図3-1のようになる。

さらに，二次電池の容量が\( \ 10 \ \mathrm {[A\cdot h]} \ \)であるから，\( \ I_{\mathrm {2}}=10 \ \mathrm {[A]} \ \)で充電するときの充電時間\( \ T_{\mathrm {c}} \ \mathrm {[h]} \ \)及び\( \ I_{\mathrm {2}}=20 \ \mathrm {[A]} \ \)で放電するときの放電時間\( \ T_{\mathrm {d}} \ \mathrm {[h]} \ \)は，
\[
\begin{eqnarray}
T_{\mathrm {c}} &=&\frac {10}{10} \\[ 5pt ] &=&1 \ \mathrm {[h]} \\[ 5pt ] T_{\mathrm {d}} &=&\frac {10}{20} \\[ 5pt ] &=&0.5 \ \mathrm {[h]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)定電流充電と定電圧充電のうち，エネルギー効率のよい充電方法
内部抵抗での損失は，電流\( \ I_{\mathrm {2}} \ \)の\( \ 2 \ \)乗に比例するため，定電圧充電の場合図3-1の\( \ t_{0} \ \)での損失が大きくなる。
したがって，一般には極端に端子電圧の高い定電流充電を除けば，定電圧充電よりも定電流充電の方がエネルギー効率が良いこととなる。