Contents
【問題】
【難易度】★★★★☆（やや難しい）
図1のようなフィードバック制御系について，次の問に答えよ。ただし，\( \ R \left( s \right) \ \)は目標値，\( \ Y \left( s \right) \ \)は出力，\( \ E \left( s \right) \ \)は偏差であり，時間信号\( \ r \left( t \right) \ \)，\( \ y \left( t \right) \ \)，\( \ e \left( t \right) \ \)をそれぞれラプラス変換したものである。
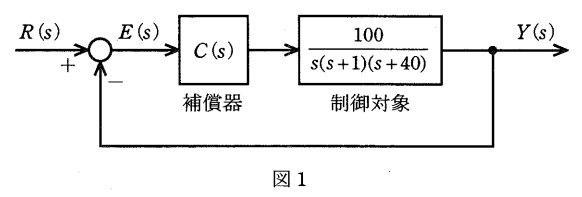
(1) 補償器を\( \ C \left( s \right) =K_{1} \ \)に選ぶとき，図1のフィードバック系の安定限界を与える\( \ K_{1} \ \)の値とそのときの持続振動の角周波数\( \ \omega _{1} \ \)を求めよ。ただし，答は平方根を含む形でよい。
(2) 図1において，\( \ C \left( s \right) =K_{1} \ \)に選び，\( \ K_{1}=1 \ \)とおく。目標値\( \ r \left( t \right) \ \)が振幅\( \ 1 \ \)，角周波数\( \ 1 \ \mathrm {[rad / s]} \ \)の正弦波信号のとき，十分に時間が経過したときの偏差\( \ e \left( t \right) \ \)の振幅を求めよ。
(3) 補償器を\( \ \displaystyle C \left( s \right) =K_{2}\frac {s+1}{s+10} \ \)に選ぶとき，この補償器の名称を答えよ。
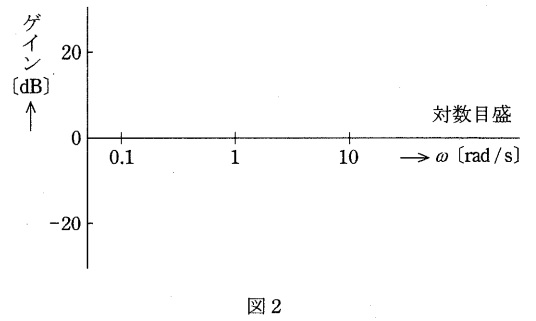
(4) 上記(3)において，\( \ K_{2}=10 \ \)のとき，補償器のゲイン（利得）特性の概形を折れ線近似で図示せよ。図2を答案用紙に書き写して答えよ。
(5) 一般に，上記(3)の補償器により改善できるフィードバック制御系の代表的な性能を述べよ。
【ワンポイント解説】
フィードバック制御系の安定限界の導出からボード線図の作図も絡めた問題です。
計算量や作業が非常に多く，時間を非常に要する問題であったかなと思います。(1)や(4)の内容が頻出となりますので，理解しておくようにしましょう。
1.ラウスの安定判別法
特性方程式\( \ a_{0}s^{n}+a_{1}s^{n-1}+a_{2}s^{n-2}+\cdots +a_{n-1}s+a_{n}=0 \ \)が与えられている時，ラウスの安定判別法による安定条件は，
\[
\begin{eqnarray}
&&1. s^{n}，s^{n-1}，\cdots ，s^{1}，s^{0}の係数がすべて存在 \\[ 5pt ]
&&2. s^{n}，s^{n-1}，\cdots ，s^{1}，s^{0}の係数がすべて同符号 \\[ 5pt ]
&&3. ラウスの数表の値がすべて正であること \\[ 5pt ]
\end{eqnarray}
\]
です。ラウスの数表は下図のようになります。
\[
\begin{array}{c|ccc}
& 1列 & 2列 & 3列 \\
\hline
1行 & a_{0} & a_{2} & a_{4} & \cdots \\
2行 & a_{1} & a_{3} & a_{5} & \cdots \\
3行 & b_{1}=\frac {a_{1}a_{2}-a_{0}a_{3}}{a_{1}} & b_{2}=\frac {a_{1}a_{4}-a_{0}a_{5}}{a_{1}} & \cdots \\
4行 & c_{1}=\frac {b_{1}a_{3}-a_{1}b_{2}}{b_{1}} & c_{2}=\frac {b_{1}a_{5}-a_{1}b_{3}}{b_{1}} & \cdots \\
\vdots & \vdots & \vdots &
\end{array}
\]
2.ボード線図
周波数伝達関数が\( \ \displaystyle W(\mathrm {j}\omega ) =\frac {K}{1+\mathrm {j}\omega T} \ \)で与えられる時，ゲイン\( \ g \ \)は，
\[
\begin{eqnarray}
g&=&20\log _{10} \left| W(\mathrm {j}\omega )\right| \\[ 5pt ]
&=&20\log _{10} \frac {K}{\sqrt {1+\left( \omega T\right) ^{2}}} \ \mathrm {[dB]} \\[ 5pt ]
\end{eqnarray}
\]
となりますが，\( \ \displaystyle \omega \ll \frac {1}{T} \ \)すなわち\( \ \omega T \ll 1 \ \)のとき，
\[
\begin{eqnarray}
g&≃&20\log _{10} \frac {K}{\sqrt {1+0}} \\[ 5pt ]
&=&20\log _{10}K \\[ 5pt ]
\end{eqnarray}
\]
とほぼ一定の値となり，\( \ \displaystyle \omega \gg \frac {1}{T} \ \)すなわち\( \ \omega T \gg 1 \ \)のとき，
\[
\begin{eqnarray}
g&≃&20\log _{10} \frac {K}{\sqrt {\left( \omega T\right) ^{2}}} \\[ 5pt ]
&=&20\log _{10} \frac {K}{\omega T} \\[ 5pt ]
&=&20\log _{10} K-20\log _{10}\omega T \\[ 5pt ]
\end{eqnarray}
\]
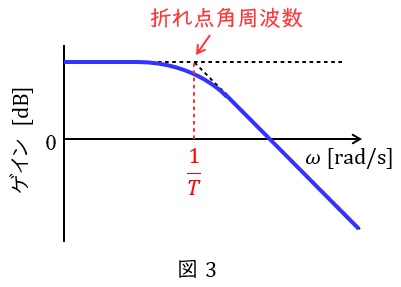
となり，横軸に対数座標をとると，ほぼ直線的に減少していくことになります。したがって，ボード線図は図3のようになります。
図3において\( \ \displaystyle \omega =\frac {1}{T} \ \)となる角周波数を折れ点角周波数と呼びます。
【解答】
(1)図1のフィードバック系の安定限界を与える\( \ K_{1} \ \)の値とそのときの持続振動の角周波数\( \ \omega _{1} \ \)
図1の関係式は，
\[
\begin{eqnarray}
R\left( s \right) -Y\left( s \right) &=&E\left( s \right) & ・・・・・・・・・ ①& \\[ 5pt ]
E\left( s \right) \cdot K_{1} \cdot \frac {100}{s\left( s+1\right) \left( s+40\right) }&=&Y\left( s \right) & ・・・・・・・・・ ②& \\[ 5pt ]
\end{eqnarray}
\]
であるので，②に①を代入すると，
\[
\begin{eqnarray}
\left\{ R\left( s \right) -Y\left( s \right) \right\} \cdot K_{1} \cdot \frac {100}{s\left( s+1\right) \left( s+40\right) }&=&Y\left( s \right) \\[ 5pt ]
100K_{1}\left\{ R\left( s \right) -Y\left( s \right) \right\} &=&s\left( s+1\right) \left( s+40\right) Y\left( s \right) \\[ 5pt ]
100K_{1}R\left( s \right) -100K_{1}Y\left( s \right) &=&s\left( s+1\right) \left( s+40\right) Y\left( s \right) \\[ 5pt ]
100K_{1}R\left( s \right) &=&\left\{ s\left( s+1\right) \left( s+40\right) +100K_{1}\right\} Y\left( s \right) \\[ 5pt ]
\frac {Y\left( s \right) }{R\left( s \right) } &=&\frac {100K_{1}}{s\left( s+1\right) \left( s+40\right) +100K_{1}} \\[ 5pt ]
&=&\frac {100K_{1}}{s^{3}+41s^{2}+40s+100K_{1}} \\[ 5pt ]
\end{eqnarray}
\]
と整理できるので，特性方程式は\( \ s^{3}+41s^{2}+40s+100K_{1}=0 \ \)となる。これに，ラウスの安定判別法を適用すると，ワンポイント解説「1.ラウスの安定判別法」の通り，
\[
\begin{array}{c|cc}
& 1列 & 2列 \\
\hline
1行 & 1 & 40 \\
2行 & 41 & 100K_{1} \\
3行 & \frac {41\times 40-1\times 100K_{1}}{41} & 0 \\
4行 & 100K_{1} & 0 \\
\end{array}
\]
となるので，\( \ 3 \ \)行\( \ 1 \ \)列より，安定となる\( \ K_{1} \ \)は，
\[
\begin{eqnarray}
\frac {41\times 40-1\times 100K_{1}}{41} &＞&0 \\[ 5pt ]
41\times 40-1\times 100K_{1} &＞&0 \\[ 5pt ]
100K_{1} &＜&1640 \\[ 5pt ]
K_{1} &＜&16.4 \\[ 5pt ]
\end{eqnarray}
\]
となり，\( \ 4 \ \)行\( \ 1 \ \)列の条件と合わせると\( \ 0＜K_{1}＜16.4 \ \)となるので，安定限界を与える\( \ K_{1} \ \)は\( \ K_{1}=0，16.4 \ \)となる。
\( \ K_{1}=0 \ \)を特性方程式に代入すれば，
\[
\begin{eqnarray}
s^{3}+41s^{2}+40s+100\times 0 &=&0 \\[ 5pt ]
s^{3}+41s^{2}+40s &=&0 \\[ 5pt ]
s\left( s^{2}+41s+40\right) &=&0 \\[ 5pt ]
s\left( s+40\right) \left( s+1\right) &=&0 \\[ 5pt ]
\end{eqnarray}
\]
となり，\( \ s=\mathrm {j}\omega \ \)を代入すると，
\[
\begin{eqnarray}
\mathrm {j}\omega\left( 40+\mathrm {j}\omega \right) \left( 1+\mathrm {j}\omega \right) &=&0 \\[ 5pt ]
\end{eqnarray}
\]
となり，\( \ \omega ＞0 \ \)より，持続振動の角周波数は存在しない。
\( \ K_{1}=16.4 \ \)を特性方程式に代入すれば，
\[
\begin{eqnarray}
s^{3}+41s^{2}+40s+100\times 16.4 &=&0 \\[ 5pt ]
s^{3}+41s^{2}+40s+1640 &=&0 \\[ 5pt ]
\end{eqnarray}
\]
となり，\( \ s=\mathrm {j}\omega \ \)を代入すると，
\[
\begin{eqnarray}
-\mathrm {j}\omega ^{3}-41\omega ^{2}+\mathrm {j}40\omega +1640 &=&0 \\[ 5pt ]
1640-41\omega ^{2}+\mathrm {j}\left( 40\omega -\omega ^{3}\right) &=&0 \\[ 5pt ]
41\left( 40-\omega ^{2}\right) +\mathrm {j}\omega \left( 40 -\omega ^{2}\right) &=&0 \\[ 5pt ]
\left( 40-\omega ^{2}\right) \left( 41+\mathrm {j}\omega \right) &=&0 \\[ 5pt ]
\left( 2\sqrt {10}-\omega \right) \left( 2\sqrt {10}+\omega \right) \left( 41+\mathrm {j}\omega \right) &=&0 \\[ 5pt ]
\end{eqnarray}
\]
となり，\( \ \omega ＞0 \ \)より，持続振動の角周波数\( \ \omega _{1} \ \)は\( \ \omega _{1} =2\sqrt {10} \ \mathrm {[rad / s]} \ \)となる。
以上から安定限界を与える\( \ K_{1}=16.4 \ \)，持続振動の角周波数\( \ \omega _{1} =2\sqrt {10} \ \mathrm {[rad / s]} \ \)と求められる。
(2)目標値\( \ r \left( t \right) \ \)が振幅\( \ 1 \ \)，角周波数\( \ 1 \ \mathrm {[rad / s]} \ \)の正弦波信号のとき，十分に時間が経過したときの偏差\( \ e \left( t \right) \ \)の振幅
①式に②式を代入し，整理すると，
\[
\begin{eqnarray}
R\left( s \right) -E\left( s \right) \cdot K_{1} \cdot \frac {100}{s\left( s+1\right) \left( s+40\right) } &=&E\left( s \right) \\[ 5pt ]
R\left( s \right) &=&E\left( s \right) +\frac {100K_{1}}{s\left( s+1\right) \left( s+40\right) }E\left( s \right) \\[ 5pt ]
&=&\frac {s\left( s+1\right) \left( s+40\right) +100K_{1}}{s\left( s+1\right) \left( s+40\right) }E\left( s \right) \\[ 5pt ]
E\left( s \right) &=&\frac {s\left( s+1\right) \left( s+40\right) }{s\left( s+1\right) \left( s+40\right) +100K_{1}}R\left( s \right) \\[ 5pt ]
&=&\frac {s^{3}+41s^{2}+40s}{s^{3}+41s^{2}+40s+100K_{1}}R\left( s \right) \\[ 5pt ]
\end{eqnarray}
\]
となる。これに，\( \ K_{1}=1 \ \)及び\( \ s=\mathrm {j}\omega =\mathrm {j} \ \)を代入すると，
\[
\begin{eqnarray}
E\left( \mathrm {j} \right) &=&\frac {-\mathrm {j}-41+\mathrm {j}40}{-\mathrm {j}-41+\mathrm {j}40+100}R\left( \mathrm {j} \right) \\[ 5pt ]
&=&\frac {-41+\mathrm {j}39}{59+\mathrm {j}39}R\left( \mathrm {j} \right) \\[ 5pt ]
\end{eqnarray}
\]
となるので，絶対値を取り，\( \ \left| R\left( \mathrm {j}\right) \right| =1 \ \)を代入すれば，
\[
\begin{eqnarray}
\left| E\left( \mathrm {j}\right) \right| &=&\left| \frac {-41+\mathrm {j}39}{59+\mathrm {j}39}R\left( \mathrm {j} \right) \right| \\[ 5pt ]
&=&\sqrt { \frac {41^{2}+39^{2}}{59^{2}+39^{2}}}\times 1 \\[ 5pt ]
&≒&0.80009 \\[ 5pt ]
\end{eqnarray}
\]
となり，偏差\( \ e \left( t \right) \ \)の振幅は\( \ 0.800 \ \)と求められる。
(3)補償器を\( \ \displaystyle C \left( s \right) =K_{2}\frac {s+1}{s+10} \ \)に選ぶとき，この補償器の名称
\( \ \displaystyle C \left( s \right) =K_{2}\frac {s+1}{s+10} \ \)の周波数伝達関数\( \ \displaystyle C \left( \mathrm {j}\omega \right) \ \)は，
\[
\begin{eqnarray}
C \left( \mathrm {j}\omega \right) &=&K_{2}\frac {1+\mathrm {j}\omega }{10+\mathrm {j}\omega } \\[ 5pt ]
&=&K_{2}\frac {1+\mathrm {j}\omega }{10+\mathrm {j}\omega }\times \frac {10-\mathrm {j}\omega }{10-\mathrm {j}\omega } \\[ 5pt ]
&=&K_{2}\frac {10+\omega ^{2}+\mathrm {j}9\omega }{100+\omega ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となるので，位相角\( \ \phi \ \)は，
\[
\begin{eqnarray}
\tan \phi &=&\frac {9\omega }{10+\omega ^{2}} \\[ 5pt ]
\phi &=&\tan ^{-1}\frac {9\omega }{10+\omega ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となり，\( \ \omega ＞0 \ \)であるから，常に\( \ \phi ＞0 \ \)となる。したがって，\( \ \displaystyle C \left( s \right) \ \)は位相進み補償器と求められる。
(4)\( \ K_{2}=10 \ \)のとき，補償器のゲイン（利得）特性の概形を折れ線近似で図示
\( \ K_{2}=10 \ \)のとき，補償器のゲイン\( \ g \ \mathrm {[dB]} \ \)は，
\[
\begin{eqnarray}
g &=&20 \log _{10} \left| C \left( \mathrm {j}\omega \right) \right| \\[ 5pt ]
&=&20 \log _{10} \left| 10\cdot \frac {1+\mathrm {j}\omega }{10+\mathrm {j}\omega } \right| \\[ 5pt ]
&=&20 \log _{10} 10\sqrt {\frac {1^{2}+\omega ^{2}}{10^{2}+\omega ^{2}}} \\[ 5pt ]
&=&20 \log _{10} 10+20\log _{10}\sqrt {\frac {1+\omega ^{2}}{100+\omega ^{2}}} \\[ 5pt ]
&=&20 +10\log _{10}\frac {1+\omega ^{2}}{100+\omega ^{2}} \\[ 5pt ]
&=&20 +10\log _{10}\left( 1+\omega ^{2}\right) -10\log _{10}\left( 100+\omega ^{2}\right) \\[ 5pt ]
\end{eqnarray}
\]
となる。上式において，\( \ \omega ≪1 \ \)のとき，
\[
\begin{eqnarray}
g &≃&20 +10\log _{10}1 -10\log _{10}100 \\[ 5pt ]
&=&20 +0 -20 \\[ 5pt ]
&=&0 \ \mathrm {[dB]} \\[ 5pt ]
\end{eqnarray}
\]
\( \ \omega =1 \ \)のとき，
\[
\begin{eqnarray}
g &≃&20 +10\log _{10}2 -10\log _{10}100 \\[ 5pt ]
&≃&0 \ \mathrm {[dB]} \\[ 5pt ]
\end{eqnarray}
\]
\( \ \omega =10 \ \)のとき，
\[
\begin{eqnarray}
g &≃&20 +10\log _{10}100 -10\log _{10}200 \\[ 5pt ]
&=&20 +10\log _{10}100 -10\log _{10}2-10\log _{10}100 \\[ 5pt ]
&≃&20 \ \mathrm {[dB]} \\[ 5pt ]
\end{eqnarray}
\]
\( \ \omega ≫10 \ \)のとき，
\[
\begin{eqnarray}
g &≃&20 +10\log _{10}\omega ^{2} -10\log _{10}\omega ^{2} \\[ 5pt ]
&=&20 \ \mathrm {[dB]} \\[ 5pt ]
\end{eqnarray}
\]
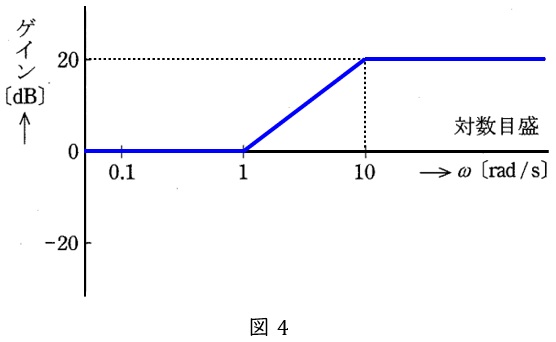
となるので，ゲイン特性の折れ線近似は図4のようになる。
※本問は折れ線近似としているため，\( \log _{10}2 \ \)が十分小さい値として近似しています。
(5)(3)の補償器により改善できるフィードバック制御系の代表的な性能
(4)のゲイン特性に示すように，一巡伝達特性（開ループ特性）の高周波域のゲインを高め，ゲイン交さ周波数を高周波域へシフトさせることにより，安定性を補償しつつ，速応性を改善できる。
愛知県出身 愛称たけちゃん
詳しくは