【問題】
【難易度】★★★★★(難しい)
定格容量\( \ \mathrm {50 \ kV\cdot A} \ \),定格一次電圧\( \ \mathrm {11 \ 000 \ V} \ \),定格二次電圧\( \ \mathrm {3 \ 300 \ V} \ \),定格周波数\( \ \mathrm {50 \ Hz} \ \)の単相変圧器があり,高圧側からの試験結果は次のとおりであった。
無負荷試験 無負荷損:\( \ P_{0}=\mathrm {290 \ W} \ \)
無負荷電流:\( \ I_{0}=\mathrm {0.221 \ A} \ \)
短絡試験 インピーダンス電圧:\( \ V_{1\mathrm {S}}=\mathrm {550 \ V} \ \)
一次電流:\( \ I_{1\mathrm {S}}=\mathrm {4.55 \ A} \ \)
インピーダンスワット:\( \ P_{\mathrm {S}}=\mathrm {740 \ W} \ \)
次の問に答えよ。
ただし,定格負荷率の力率\( \ \cos \phi \ \)における電圧の変動率\( \ \varepsilon [ % ] \ \)は,百分率抵抗降下を\( \ p \ [ % ] \ \),百分率リアクタンス降下を\( \ q \ [ % ] \ \)とすれば,次式で表せるものとする。
\[
\varepsilon =p \cos \phi +q \sin \phi +\frac {1}{200}\left( q \cos \phi -p \sin \phi \right) ^{2} \ [ % ]
\]
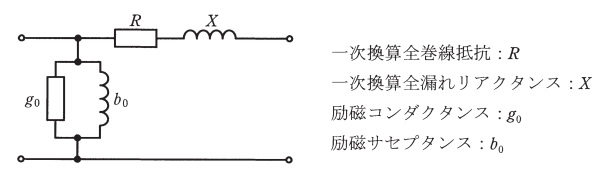
(1) 図に示す簡易等価回路の回路定数(一次側換算値)をそれぞれ求めよ。
(2) 遅れ力率\( \ 80 \ % \ \),全負荷における電圧の変動率を求めよ。
(3) 遅れ力率\( \ 80 \ % \ \),\( \ \displaystyle \frac {1}{2} \ \)負荷における効率を求めよ。
(4) 遅れ力率\( \ 80 \ % \ \),\( \ \displaystyle \frac {1}{2} \ \)負荷における電圧の変動率を求めよ。
【ワンポイント解説】
解法はそれほど複雑ではありませんが,途中の計算がとても面倒な問題です。解法のみでなく途中の計算での有効数字の取り方等をよく理解しましょう。ただし,本問は全設問を解くと非常に時間がかかるので,他の問がわからない場合のみ選択した方が良いと思います。
1.百分率抵抗降下\( \ p \ \),百分率リアクタンス降下\( \ q \ \)
\( \ Z=R+jX \ \)で表されるインピーダンスの百分率インピーダンス降下\( \ %Z \ \),百分率抵抗降下\( \ p \ \),百分率リアクタンス降下\( \ q \ \)は,
\[
\begin{eqnarray}
%Z&=&\frac {Z}{Z_{\mathrm {B}}}\times 100 = \frac {ZI_{1\mathrm {n}}}{V_{1\mathrm {n}}}\times 100 \ [ % ] \\[ 5pt ]
p&=&\frac {R}{Z_{\mathrm {B}}}\times 100 = \frac {RI_{1\mathrm {n}}}{V_{1\mathrm {n}}}\times 100 \ [ % ] \\[ 5pt ]
q&=&\frac {X}{Z_{\mathrm {B}}}\times 100 = \frac {XI_{1\mathrm {n}}}{V_{1\mathrm {n}}}\times 100 \ [ % ]
\end{eqnarray}
\]
となります。
【関連する「電気の神髄」記事】
【解答】
(1)簡易等価回路の回路定数
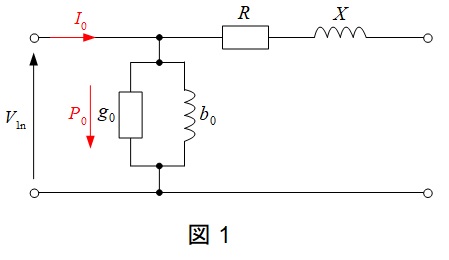
無負荷試験は,図1のように定格一次電圧\( \ V_{1\mathrm {n}} \ \)を加えた時,二次側が無負荷(開放)である時の試験であるから,
\[
\begin{eqnarray}
P_{0}&=&g_{0}V_{1\mathrm {n}}^{2} &・・・・・・・・・・①& \\[ 5pt ]
I_{0}&=&\sqrt {g_{0}^{2}+b_{0}^{2}}V_{1\mathrm {n}} &・・・・・・・・・・②&
\end{eqnarray}
\]
という関係が成立する。①に各値を代入すると,
\[
\begin{eqnarray}
290&=&g_{0}\times 11000^{2} \\[ 5pt ]
g_{0}&=&\frac {290}{11000^{2}} \\[ 5pt ]
&≒&2.3967\times 10^{-6} \ [ \mathrm {S} ] → 2.40 \ [ \mathrm {\mu S} ]
\end{eqnarray}
\]
と求められる。次に②を\( \ b_{0} \ \)について整理して,各値を代入すると,
\[
\begin{eqnarray}
I_{0}&=&\sqrt {g_{0}^{2}+b_{0}^{2}}V_{1\mathrm {n}} \\[ 5pt ]
\sqrt {g_{0}^{2}+b_{0}^{2}}&=&\frac {I_{0}}{V_{1\mathrm {n}}} \\[ 5pt ]
g_{0}^{2}+b_{0}^{2}&=&\left( \frac {I_{0}}{V_{1\mathrm {n}}}\right) ^{2} \\[ 5pt ]
b_{0}^{2}&=&\left( \frac {I_{0}}{V_{1\mathrm {n}}}\right) ^{2}-g_{0}^{2} \\[ 5pt ]
b_{0}&=&\sqrt {\left( \frac {I_{0}}{V_{1\mathrm {n}}}\right) ^{2}-g_{0}^{2}} \\[ 5pt ]
&=&\sqrt {\left( \frac {0.221}{11000}\right) ^{2}-\left( 2.3967\times 10^{-6}\right) ^{2}} \\[ 5pt ]
&≒&\sqrt {\left( 20.091\times 10^{-6}\right) ^{2}-\left( 2.3967\times 10^{-6}\right) ^{2}} \\[ 5pt ]
&≒& 19.947\times 10^{-6} \ [ \mathrm {S} ] → 19.9 \ [ \mathrm {\mu S} ]
\end{eqnarray}
\]
と求められる。
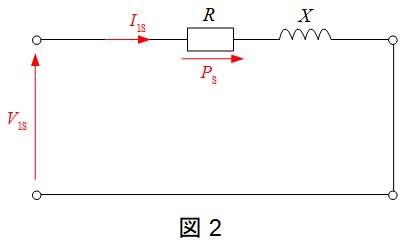
短絡試験は図2のように,二次側を短絡し,二次側に定格電流を流すように一次電圧を調整した試験であるから,
\[
\begin{eqnarray}
P_{\mathrm {S}}&=&RI_{1\mathrm {S}}^{2} &・・・・・・・・・・③& \\[ 5pt ]
V_{1\mathrm {S}}&=&\sqrt {R^{2}+X^{2}}I_{1\mathrm {S}} &・・・・・・・・・・④&
\end{eqnarray}
\]
という関係が成立する。③に各値を代入すると,
\[
\begin{eqnarray}
740&=&R\times 4.55^{2} \\[ 5pt ]
R&=&\frac {740}{4.55^{2}} \\[ 5pt ]
&≒&35.744 → 35.7 \ [ \Omega ]
\end{eqnarray}
\]
と求められる。次に④を\( \ X \ \)について整理して,各値を代入すると,
\[
\begin{eqnarray}
V_{1\mathrm {S}}&=&\sqrt {R^{2}+X^{2}}I_{1\mathrm {S}} \\[ 5pt ]
\sqrt {R^{2}+X^{2}}&=&\frac {V_{1\mathrm {S}}}{I_{1\mathrm {S}}} \\[ 5pt ]
R^{2}+X^{2}&=&\left( \frac {V_{1\mathrm {S}}}{I_{1\mathrm {S}}}\right) ^{2} \\[ 5pt ]
X^{2}&=&\left( \frac {V_{1\mathrm {S}}}{I_{1\mathrm {S}}}\right) ^{2}-R^{2} \\[ 5pt ]
X&=&\sqrt {\left( \frac {V_{1\mathrm {S}}}{I_{1\mathrm {S}}}\right) ^{2}-R^{2}} \\[ 5pt ]
&=&\sqrt {\left( \frac {550}{4.55}\right) ^{2}-\left( 35.744\right) ^{2}} \\[ 5pt ]
&≒&\sqrt {14612-1277.6} \\[ 5pt ]
&≒& 115.47 → 115 \ [ \Omega ]
\end{eqnarray}
\]
と求められる。
(2)遅れ力率\( \ 80 \ % \ \),全負荷における電圧の変動率
単相変圧器においては定格容量\( \ S_{\mathrm {n}} \ \),定格一次電圧\( \ V_{1\mathrm {n}} \ \)とすると,定格一次電流\( \ I_{1\mathrm {n}} \ \)は,
\[
\begin{eqnarray}
I_{1\mathrm {n}}&=&\frac {S_{\mathrm {n}}}{V_{\mathrm {1n}}} \\[ 5pt ]
&=&\frac {50000}{11000} \\[ 5pt ]
&=&4.5455 \ [ \mathrm {A} ]
\end{eqnarray}
\]
であるから,ワンポイント解説「1.百分率抵抗降下\( \ p \ \),百分率リアクタンス降下\( \ q \ \)」より,
\[
\begin{eqnarray}
p&=&\frac {RI_{1\mathrm {n}}}{V_{1\mathrm {n}}}\times 100 \\[ 5pt ]
&=&\frac {35.744\times 4.5455}{11000}\times 100 \\[ 5pt ]
&=&1.4770 \ [ % ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
q&=&\frac {XI_{1\mathrm {n}}}{V_{1\mathrm {n}}}\times 100 \\[ 5pt ]
&=&\frac {115.47\times 4.5455}{11000}\times 100 \\[ 5pt ]
&=&4.7715 \ [ % ]
\end{eqnarray}
\]
と求められる。また,題意より\( \ \cos \phi =0.8 \ \),\( \ \sin \phi =\sqrt {1-0.8^{2}}=0.6 \ \)であるから,電圧の変動率\( \ \varepsilon \ \)は,
\[
\begin{eqnarray}
\varepsilon &=&p \cos \phi +q \sin \phi +\frac {1}{200}\left( q \cos \phi -p \sin \phi \right) ^{2} \\[ 5pt ]
&=&1.4770\times 0.8 +4.7715\times 0.6 +\frac {1}{200}\left( 4.7715 \times 0.8 -1.4770\times 0.6 \right) ^{2} \\[ 5pt ]
&=&1.1816 +2.8629 +\frac {1}{200}\left( 3.8172 -0.8862 \right) ^{2} \\[ 5pt ]
&≒&1.1816 +2.8629 + 0.042954 \\[ 5pt ]
&≒&4.0875 → 4.09 \ [ % ]
\end{eqnarray}
\]
と求められる。
(3)遅れ力率\( \ 80 \ % \ \),\( \ \displaystyle \frac {1}{2} \ \)負荷における効率
全負荷での出力を\( \ P_{\mathrm {n}} \ \)とすると,
\[
\begin{eqnarray}
P_{\mathrm {n}} &=&S_{\mathrm {n}} \cos \phi \\[ 5pt ]
&=&50 \times 0.8 \\[ 5pt ]
&=&40 \ [ \mathrm {kW} ]
\end{eqnarray}
\]
であり,\( \ \displaystyle \frac {1}{2} \ \)負荷での出力は\( \ \displaystyle \frac {1}{2}P_{\mathrm {n}} \ \),銅損は\( \ \displaystyle \left( \frac {1}{2}\right) ^{2}P_{\mathrm {S}} \ \),鉄損は\( \ P_{0} \ \)となるので,\( \ \displaystyle \frac {1}{2} \ \)負荷での効率\( \ \eta \ \)は,
\[
\begin{eqnarray}
\eta &=&\frac {\displaystyle \frac {1}{2}P_{\mathrm {n}}}{\displaystyle \frac {1}{2}P_{\mathrm {n}}+\left( \frac {1}{2}\right) ^{2}P_{\mathrm {S}}+P_{0}} \times 100 \\[ 5pt ]
&=&\frac {\displaystyle \frac {1}{2}\times 40000}{\displaystyle \frac {1}{2}\times 40000+\left( \frac {1}{2}\right) ^{2}\times 740+290} \times 100 \\[ 5pt ]
&=&97.680 → 97.7 \ [ % ]
\end{eqnarray}
\]
と求められる。
(4)遅れ力率\( \ 80 \ % \ \),\( \ \displaystyle \frac {1}{2} \ \)負荷における電圧の変動率
負荷が\( \ \displaystyle \frac {1}{2} \ \)となると,定格一次電流が\( \ \displaystyle \frac {1}{2} \ \)となり,ワンポイント解説「1.百分率抵抗降下\( \ p \ \),百分率リアクタンス降下\( \ q \ \)」より各百分率降下は定格一次電流に比例するので,設問の電圧変動率の式の\( \ p \ \)と\( \ q \ \)をそれぞれ\( \ \displaystyle \frac {1}{2}p \ \),\( \ \displaystyle \frac {1}{2}q \ \)とすればよい。よって,求める電圧変動率\( \ \varepsilon ^{\prime } \ \)は,
\[
\begin{eqnarray}
\varepsilon ^{\prime }&=&\frac {1}{2}p \cos \phi +\frac {1}{2}q \sin \phi +\frac {1}{200}\left( \frac {1}{2}q \cos \phi -\frac {1}{2}p \sin \phi \right) ^{2} \\[ 5pt ]
&=&\frac {1}{2}\times 1.4770\times 0.8 +\frac {1}{2}\times 4.7715\times 0.6 +\frac {1}{200}\left( \frac {1}{2}\times 4.7715 \times 0.8 -\frac {1}{2}\times 1.4770\times 0.6 \right) ^{2} \\[ 5pt ]
&≒&0.5908 +1.4315 +\frac {1}{800}\left( 3.8172 -0.8862 \right) ^{2} \\[ 5pt ]
&≒&0.5908 +1.4315 + 0.010738 \\[ 5pt ]
&≒&2.0330 → 2.03 \ [ % ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは