《機械・制御》〈回転機〉[R01:問1]三相かご形誘導電動機に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

三相かご形誘導電動機に関して，次の問に答えよ。

定格出力\( \ 5 \ \mathrm {kW} \ \)，定格電圧\( \ 200 \ \mathrm {V} \ \)，\( \ 4 \ \)極の三相かご形誘導電動機がある。この電動機を\( \ 50 \ \mathrm {Hz} \ \)の電源に接続して全負荷運転したとき，速度は\( \ 1440 \ \mathrm {{min}^{-1}} \ \)である。また，この電動機の鉄損は\( \ 180 \ \mathrm {W} \ \)であった。一次巻線の抵抗を\( \ r_{1} \ \)，一次側に換算した二次巻線の抵抗を\( \ r_{2}^{\prime } \ \)としたとき，それらの比が\( \ \displaystyle \frac {r_{1}}{r_{2}^{\prime }}=\frac {2}{5} \ \)であった。簡易等価回路を用いて，この電動機の次の値を求めよ。ただし，機械損は無視する。

(1)　同期速度\( \ \mathrm {[{min}^{-1}]} \ \)

(2)　全負荷時の滑り

(3)　全負荷時の滑り周波数\( \ \mathrm {[Hz]} \ \)

(4)　全負荷時のトルク\( \ \mathrm {[N\cdot m]} \ \)

(5)　全負荷時の効率\( \ \mathrm {[％]} \ \)

【ワンポイント解説】

誘導電動機の問題は\( \ \mathrm {L} \ \)形等価回路を描けるかどうかが最も重要となってきます。本問の場合は(3)の滑り周波数の定義を知っているかどうかが完答の分かれ目になるかもしれません。パターン化されている内容も多いため，多くの受験生が選択する問題と言えるので，確実に解けるようにしておきましょう。

1.電動機の同期速度\(N_{\mathrm {s}}\)
定格周波数が\( \ f \ \mathrm {[Hz]} \ \)，極数が\( \ p \ \)の電動機の同期速度\( \ N_{\mathrm {s}} \ \mathrm {[min^{-1}]} \ \)は，
\[
\begin{eqnarray}
N_{\mathrm {s}}&=&\frac {120f}{p} \\[ 5pt ] \end{eqnarray}
\] となります。

2.誘導機の滑り\( \ s \ \)
誘導機の同期速度が\( \ N_{\mathrm {s}} \ \)，回転数が\( \ N \ \)である時，誘導機の滑り\( \ s \ \)は，
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}
\] となります。

3.電動機の同期角速度\( \ \omega _{\mathrm {s}} \ \)
同期速度が\( \ N_{\mathrm {s}} \ \)の電動機の同期角速度\( \ \omega _{\mathrm {s}} \ \)は，
\[
\begin{eqnarray}
\omega _{\mathrm {s}}&=&\frac {2\pi N_{\mathrm {s}}}{60} \\[ 5pt ] \end{eqnarray}
\]

4.誘導電動機の出力\( \ P_{\mathrm {o}} \ \)とトルク\( \ T \ \)の関係
電動機の出力\( \ P_{\mathrm {o}} \ \)，角速度\( \ \omega \ \)，電動機の二次入力を\( \ P_{2} \ \)，同期角速度\( \ \omega _{\mathrm {s}} \ \)とすると，電動機のトルク\( \ T \ \)は，
\[
\begin{eqnarray}
T&=&\frac {P_{\mathrm {o}}}{\omega } \\[ 5pt ] &=&\frac {P_{2}\left( 1-s \right) }{\omega _{\mathrm {s}}\left( 1-s \right) } \\[ 5pt ] &=&\frac {P_{2}}{\omega _{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}
\] で求められます。

5.二次入力\( \ P_{2} \ \)と出力\( \ P_{\mathrm {o}} \ \)と二次銅損\( \ P_{\mathrm {c2}} \ \)の関係
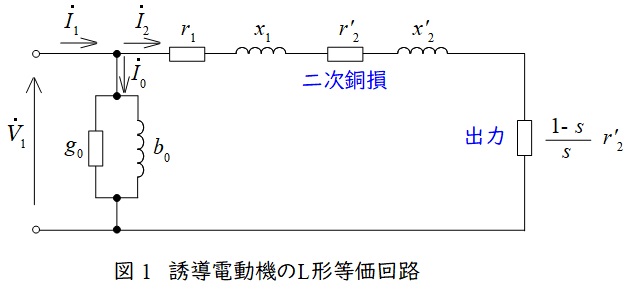
誘導電動機の\( \ \mathrm {L} \ \)形等価回路は図1のようになります。図1において，\( \ {\dot V}_{1} \ \)は一次側端子電圧，\( \ {\dot I}_{1} \ \)は一次電流，\( \ {\dot I}_{2} \ \)は二次電流，\( \ {\dot I}_{0} \ \)は励磁電流，\( \ r_{1} \ \)は一次巻線抵抗，\( \ r_{2}^{\prime } \ \)は二次巻線抵抗の一次換算，\( \ x_{1} \ \)は一次漏れリアクタンス，\( \ x_{2}^{\prime } \ \)は二次漏れリアクタンスの一次換算，\( \ s \ \)は滑りとなります。
図1より，出力\( \ P_{\mathrm {o}} \ \)，二次銅損\( \ P_{\mathrm {c2}} \ \)，二次入力\( \ P_{2} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {o}} &=& 3\frac {1-s}{s}r_{2}^{\prime }I_{2}^{2} \\[ 5pt ] P_{\mathrm {c2}} &=& 3r_{2}^{\prime }I_{2}^{2} \\[ 5pt ] P_{2} &=& P_{\mathrm {o}}+P_{\mathrm {c2}} =3\frac {r_{2}^{\prime }}{s}I_{2}^{2} \\[ 5pt ] \end{eqnarray}
\] となり，誘導電動機の二次入力\( \ P_{2} \ \)，出力\( \ P_{\mathrm {o}} \ \)，二次銅損\( \ P_{\mathrm {c2}} \ \)には，
\[
\begin{eqnarray}
P_{2}：P_{\mathrm {o}}：P_{\mathrm {c2}} &=& 1：(1-s)：s \\[ 5pt ] \end{eqnarray}
\] の関係があることが分かります。

6.誘導電動機の効率\( \ \eta \ \)
一次入力\( \ P_{\mathrm {1}} \ \)，出力\( \ P_{\mathrm {o}} \ \)，一次銅損\( \ P_{\mathrm {c1}} \ \)，二次銅損\( \ P_{\mathrm {c2}} \ \)，鉄損\( \ P_{\mathrm {i}} \ \)とすると，誘導電動機の効率\( \ \eta \ \)は，
\[
\begin{eqnarray}
\eta &=&\frac {P_{\mathrm {o}}}{P_{\mathrm {1}}}\times 100 \\[ 5pt ] &=&\frac {P_{\mathrm {o}}}{P_{\mathrm {o}}+P_{\mathrm {i}}+P_{\mathrm {c1}}+P_{\mathrm {c2}}}\times 100 \\[ 5pt ] \end{eqnarray}
\] で求められます。

【解答】

(1)同期速度\( \ \mathrm {[{min}^{-1}]} \ \)
ワンポイント解説「1.電動機の同期速度\(N_{\mathrm {s}}\)」より，
\[
\begin{eqnarray}
N_{\mathrm {s}}&=&\frac {120f}{p} \\[ 5pt ] &=&\frac {120\times 50}{4} \\[ 5pt ] &=&1500 \ \mathrm {[{min}^{-1}]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)全負荷時の滑り
ワンポイント解説「2.誘導機の滑り\( \ s \ \)」より，
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ] &=&\frac {1500-1440}{1500} \\[ 5pt ] &=&0.04 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)全負荷時の滑り周波数\( \ \mathrm {[Hz]} \ \)
滑り周波数を\( \ f_{2} \ \)とすると，\( \ f_{2}=sf \ \)となるので，
\[
\begin{eqnarray}
f_{2}&=&sf \\[ 5pt ] &=&0.04\times 50 \\[ 5pt ] &=&2.00 \ \mathrm {[Hz]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)全負荷時のトルク\( \ \mathrm {[N\cdot m]} \ \)
ワンポイント解説「4.誘導電動機の出力\( \ P_{\mathrm {o}} \ \)とトルク\( \ T \ \)の関係」より，
\[
\begin{eqnarray}
T&=&\frac {P_{\mathrm {o}}}{\omega } \\[ 5pt ] \end{eqnarray}
\] となる。ここで，角速度\( \ \omega \ \)は，
\[
\begin{eqnarray}
\omega &=&\frac {2\pi N}{60} \\[ 5pt ] &=&\frac {2\pi \times 1440}{60} \\[ 5pt ] &≒&150.80 \ \mathrm {[rad/s]} \\[ 5pt ] \end{eqnarray}
\] であるから，トルク\( \ T \ \)は，
\[
\begin{eqnarray}
T&=&\frac {5000}{150.80} \\[ 5pt ] &≒&33.156　→　33.2 \ \mathrm {[N\cdot m]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)全負荷時の効率\( \ \mathrm {[％]} \ \)
ワンポイント解説「5.二次入力\( \ P_{2} \ \)と出力\( \ P_{\mathrm {o}} \ \)と二次銅損\( \ P_{\mathrm {c2}} \ \)の関係」より，二次銅損\( \ P_{\mathrm {c2}} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {c2}}&=&\frac {s}{1-s}P_{\mathrm {o}} \\[ 5pt ] &=&\frac {0.04}{1-0.04}\times 5000 \\[ 5pt ] &≒&208.33 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] となる。図1の\( \ \mathrm {L} \ \)形等価回路より，一次銅損\( \ P_{\mathrm {c1}} \ \)を\( \ P_{\mathrm {c2}} \ \)で表すと，
\[
\begin{eqnarray}
P_{\mathrm {c1}}&=&3r_{1}I_{2}^{2} \\[ 5pt ] &=&3\times \frac {2}{5}r_{2}^{\prime }I_{2}^{2} \\[ 5pt ] &=&\frac {2}{5}P_{\mathrm {c2}} \\[ 5pt ] &=&\frac {2}{5}\times 208.33 \\[ 5pt ] &≒&83.332 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] となるので，全体の効率\( \ \eta \ \)は，
\[
\begin{eqnarray}
\eta &=&\frac {P_{\mathrm {o}}}{P_{\mathrm {o}}+P_{\mathrm {i}}+P_{\mathrm {c1}}+P_{\mathrm {c2}}}\times 100 \\[ 5pt ] &=&\frac {5000}{5000+180+83.332+208.33}\times 100 \\[ 5pt ] &≒&91.380　→　91.4 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] と求められる。