《機械・制御》〈パワーエレクトロニクス〉[R05:問3]電力用能動フィルタに関する論説・計算問題

【問題】

【難易度】★★★☆☆（普通）

以下の文章は，負荷の発生する高調波を除去する電力用能動フィルタに関するものである。次の問に答えよ。

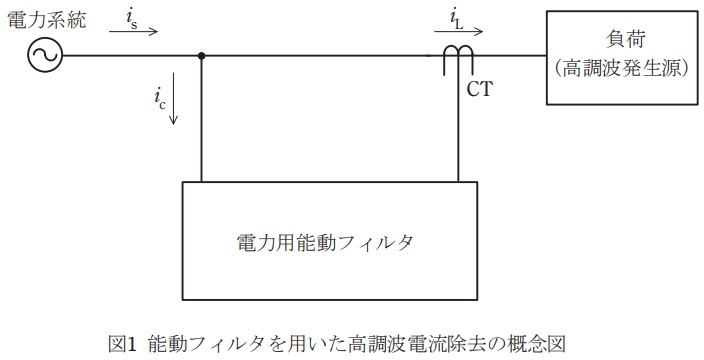
図1は能動フィルタを用いた高調波電流除去の概念図である。電力系統から流出する電源電流を\( \ i_{\mathrm {s}} \ \)とし，電力系統の高調波に対するインピーダンスは十分小さく無視できるものとする。負荷電流\( \ i_{\mathrm {L}} \ \)は基本波成分\( \ i_{\mathrm {1}} \ \)と高調波成分\( \ i_{\mathrm {H}} \ \)の和\( \ i_{\mathrm {L}}=i_{\mathrm {1}}+i_{\mathrm {H}} \ \)であるとする。能動フィルタは，補償電流\( \ i_{\mathrm {c}} \ \)を制御して\( \ i_{\mathrm {s}} \ \)を\( \ i_{\mathrm {1}} \ \)のみとなるようにする。

(1)　高調波を発生する半導体デバイスを用いた電力変換装置の名称を一つ挙げよ。

(2)　系統に高調波が存在する場合，系統に接続された他の機器にどのような影響が生じるか，\( \ 20 \ \)文字以内で述べよ。

(3)　\( \ i_{\mathrm {s}} \ \)を\( \ i_{\mathrm {1}} \ \)のみにするための\( \ i_{\mathrm {c}} \ \)の式を示せ。

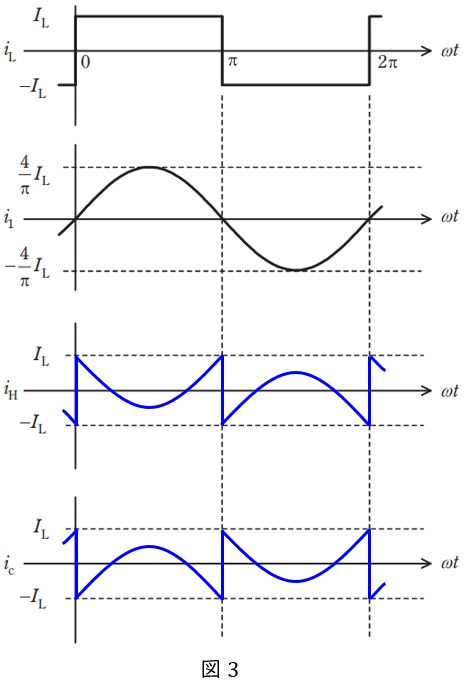
(4)　図で示す\( \ i_{\mathrm {L}} \ \)の波形が最大値\( \ I_{\mathrm {L}} \ \)と最小値\( \ -I_{\mathrm {L}} \ \)の\( \ 2 \ \)レベル矩形波であるとき，\( \ i_{\mathrm {1}} \ \)の振幅は\( \ \displaystyle \frac {4}{\pi }I_{\mathrm {L}} \ \)である。このとき，答案用紙に図2と同じ図が印刷されているので，\( \ i_{\mathrm {H}} \ \)，\( \ i_{\mathrm {c}} \ \)の波形を大小・正負が明らかになるように図示せよ。

(5)　\( \ i_{\mathrm {L}} \ \)，\( \ i_{\mathrm {1}} \ \)，\( \ i_{\mathrm {c}} \ \)の実効値を，それぞれ\( \ I_{\mathrm {L}} \ \)を用いて表せ。なお，\( \ i_{\mathrm {c}} \ \)の実効値を求めるときは，ひずみ波の実効値は直流分及び各調波の実効値の\( \ 2 \ \)乗の和の平方根であることを用いても良い。

【ワンポイント解説】

高調波を除去する電力用能動フィルタの原理に関する問題です。
(1)，(2)が電力管理科目の論説問題のような内容で，(3)以降もそれほど難解な計算はないので，例年のパワーエレクトロニクスの問題に比べれば取り組みやすい問題であったかと思います。

1.高調波
「高圧又は特別高圧で受電する需要家の高調波抑制対策ガイドライン」では高調波環境目標レベルとして\( \ 6.6 \ \mathrm {kV} \ \)配電系統で\( \ 5 \ \mathrm {％} \ \)，特別高圧系統で\( \ 3 \ \mathrm {％} \ \)を維持すると定められています。

①高調波の発生源
アーク炉等の負荷，変圧器の磁気飽和，パワーエレクトロニクス機器等。
\( \ 3 \ \)次，\( \ 5 \ \)次，\( \ 7 \ \)次，\( \ 11 \ \)次の奇数次の高調波が多く，偶数次では\( \ 2 \ \)次の高調波も発生します。\( \ 3 \ \)次の高調波は変圧器の\( \ \Delta \ \)結線で還流させることができるので，電力系統としては最も多い\( \ 5 \ \)次の高調波に対する対策を行います。

②高調波による影響
・コンデンサやリアクトルが過熱，焼損
・電力用ヒューズのエレメントが過熱，溶断
・変圧器が振動，過熱
・発電機の巻線が過熱
・保護継電器が誤動作
・配電用遮断器が誤トリップ
・ラジオやテレビに可聴雑音が発生
・半導体機器が故障及び性能劣化

③高調波の対策
・整流器の相数を増加する
・電力用コンデンサには必ず直列リアクトルを設置する
・パッシブフィルタ，アクティブフィルタを設置する
・短絡容量の大きな系統から受電する

2.平均値と実効値の定義
\( \ f( \theta ) \ \)を周期\( \ T \ \)の周期関数であるとしたとき，平均値と実効値は以下の通りとなります。
①平均値\( \ F_{\mathrm {av}} \ \)
定義式は，
\[
\begin{eqnarray}
F_{\mathrm {av}}&=&\frac {1}{T}\int _{0}^{T}f( \theta ) \mathrm {d}\theta \\[ 5pt ] \end{eqnarray}
\] であり，これを正弦波\( \ v\left( t \right) =V_{\mathrm {m}}\sin \omega t \ \)に適用すると，
\[
\begin{eqnarray}
V_{\mathrm {av}} &=&\frac {1}{\pi }\int _{0}^{\pi }V_{\mathrm {m}}\sin \omega t \mathrm {d}\omega t \\[ 5pt ] &=&\frac {V_{\mathrm {m}}}{\pi }\left[ -\cos \omega t \right] _{0}^{\pi } \\[ 5pt ] &=&\frac {V_{\mathrm {m}}}{\pi }\left[ 1+1 \right] \\[ 5pt ] &=&\frac {2}{\pi }V_{\mathrm {m}}
\end{eqnarray}
\] となります。

②実効値\( \ F \ \)　
定義式は，
\[
\begin{eqnarray}
F&=&\sqrt {\frac {1}{T} \int _{0}^{T} f( \theta ) ^{2} \mathrm {d}\theta } \\[ 5pt ] \end{eqnarray}
\] であり，これを正弦波\( \ v\left( t \right) =V_{\mathrm {m}}\sin \omega t \ \)に適用すると，
\[
\begin{eqnarray}
V &=&\sqrt {\frac {1}{\pi }\int _{0}^{\pi }{V_{\mathrm {m}}}^{2}\sin ^{2}\omega t \mathrm {d}\omega t} \\[ 5pt ] &=&V_{\mathrm {m}}\sqrt {\frac {1}{\pi }\int _{0}^{\pi }\frac {1-\cos 2\omega t}{2} \mathrm {d}\omega t} \\[ 5pt ] &=&V_{\mathrm {m}}\sqrt {\frac {1}{\pi }\left[ \frac {1}{2}\omega t -\frac {1}{4}\sin 2\omega t \right] _{0}^{\pi } } \\[ 5pt ] &=&V_{\mathrm {m}}\sqrt {\frac {1}{\pi }\left[ \frac {1}{2}\pi -0 -0 +0 \right] _{0}^{\pi } } \\[ 5pt ] &=&\frac {V_{\mathrm {m}}}{\sqrt {2}}
\end{eqnarray}
\] となります。

【解答】

(1)高調波を発生する半導体デバイスを用いた電力変換装置の名称
(ポイント)
・高調波はスイッチング素子が絡む電力変換装置で多く発生します。
・交流⇄直流変換では特に多くなり，整流回路，インバータ，サイクロコンバータ等は全て正答と言えるでしょう。

(試験センター解答例)
ダイオード整流器・変換器，サイリスタ整流器・変換器，インバータ，など。

(2)系統に高調波が存在する場合，系統に接続された他の機器にどのような影響が生じるか
(ポイント)
・ワンポイント解説「1.高調波」の通りです。

(試験センター解答例)
コンデンサやリアクトルの過熱や振動，コンピュータや電子機器の誤作動，など。

(3)\( \ i_{\mathrm {s}} \ \)を\( \ i_{\mathrm {1}} \ \)のみにするための\( \ i_{\mathrm {c}} \ \)の式
題意より\( \ i_{\mathrm {L}}=i_{\mathrm {1}}+i_{\mathrm {H}} \ \)であり，図1より\( \ i_{\mathrm {L}}=i_{\mathrm {s}}-i_{\mathrm {c}} \ \)であるから，
\[
\begin{eqnarray}
i_{\mathrm {s}}-i_{\mathrm {c}}&=&i_{\mathrm {1}}+i_{\mathrm {H}} \\[ 5pt ] \end{eqnarray}
\] となる。したがって，\( \ i_{\mathrm {s}}=i_{\mathrm {1}} \ \)となるように制御するので，
\[
\begin{eqnarray}
i_{\mathrm {1}}-i_{\mathrm {c}}&=&i_{\mathrm {1}}+i_{\mathrm {H}} \\[ 5pt ] -i_{\mathrm {c}}&=&i_{\mathrm {H}} \\[ 5pt ] i_{\mathrm {c}}&=&-i_{\mathrm {H}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)\( \ i_{\mathrm {H}} \ \)，\( \ i_{\mathrm {c}} \ \)の波形を大小・正負が明らかになるように図示
題意より，\( \ i_{\mathrm {L}}=i_{\mathrm {1}}+i_{\mathrm {H}} \ \)すなわち\( \ i_{\mathrm {H}}=i_{\mathrm {L}}-i_{\mathrm {1}} \ \)であり，(3)より，\( \ i_{\mathrm {c}}=-i_{\mathrm {H}} \ \)なので，図3のように描くことができる。

(5)\( \ i_{\mathrm {L}} \ \)，\( \ i_{\mathrm {1}} \ \)，\( \ i_{\mathrm {c}} \ \)の実効値
実効値の定義より，\( \ i_{\mathrm {L}} \ \)の実効値\( \ I_{\mathrm {Le}} \ \)は，ワンポイント解説「2.平均値と実効値の定義」の通り，
\[
\begin{eqnarray}
I_{\mathrm {Le}} &=&\sqrt {\frac {1}{\pi }\int _{0}^{\pi }{I_{\mathrm {L}}}^{2} \mathrm {d}\omega t} \\[ 5pt ] &=&\sqrt {\frac {1}{\pi }\left[ {I_{\mathrm {L}}}^{2} \omega t\right] _{0}^{\pi }} \\[ 5pt ] &=&\sqrt {\frac {1}{\pi }\cdot {I_{\mathrm {L}}}^{2} \pi } \\[ 5pt ] &=&\sqrt { {I_{\mathrm {L}}}^{2} } \\[ 5pt ] &=&I_{\mathrm {L}} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ i_{\mathrm {1}} \ \)の実効値\( \ I_{\mathrm {1e}} \ \)は，ワンポイント解説「2.平均値と実効値の定義」の通り，
\[
\begin{eqnarray}
I_{\mathrm {1e}} &=&\frac {1}{\sqrt {2}}\frac {4}{\pi }I_{\mathrm {L}} \\[ 5pt ] &=&\frac {2\sqrt {2}}{\pi }I_{\mathrm {L}} \\[ 5pt ] &≒&0.90032I_{\mathrm {L}}　→　0.900I_{\mathrm {L}} \\[ 5pt ] \end{eqnarray}
\] と求められる。題意より，ひずみ波の実効値は直流分及び各調波の実効値の\( \ 2 \ \)乗の和の平方根であるので，\( \ i_{\mathrm {c}} \ \)の実効値\( \ I_{\mathrm {ce}} \ \)は，\( \ {I_{\mathrm {Le}}}^{2}={I_{\mathrm {1e}}}^{2}+{I_{\mathrm {ce}}}^{2} \ \)の関係より，
\[
\begin{eqnarray}
I_{\mathrm {ce}} &=&\sqrt {{I_{\mathrm {Le}}}^{2}-{I_{\mathrm {1e}}}^{2}} \\[ 5pt ] &=&\sqrt {{I_{\mathrm {L}}}^{2}-\left( 0.90032I_{\mathrm {L}}\right) ^{2}} \\[ 5pt ] &≒&0.435I_{\mathrm {L}} \\[ 5pt ] \end{eqnarray}
\] と求められる。