Contents
【問題】
【難易度】★★★★☆(やや難しい)
本問題で扱う伝達関数の全ての極と零点は複素平面上の右半平面には存在しないものと仮定する。以下の問に答えよ。ここで必要に応じて,\( \ 14=20 \log _{10} 10^{0.7} \ \),\( \ 10^{0.7}=5.0119 \ \)を用いよ。ただし,全ての図は折れ線近似で表している。
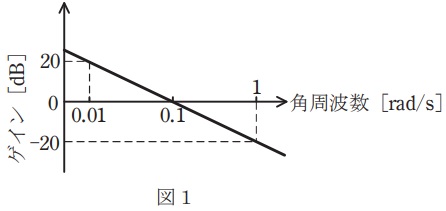
(1) 図1に示すゲイン特性曲線から積分要素の伝達関数\( \ \displaystyle G_{1}\left( s\right) =\frac {1}{T_{\mathrm {I}}s} \ \)を求めよ。
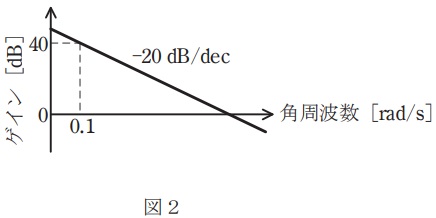
(2) 図2に示すゲイン特性曲線が表す伝達関数\( \ G \left( s\right) \ \)を\( \ G \left( s\right) =G_{1} \left( s\right) G_{2} \left( s\right) \ \)のように分解して考える。\( \ G_{1} \left( s\right) \ \)を小問(1)で求めた伝達関数とするときの\( \ G_{2} \left( s\right) \ \)を求めよ。
(3) 図2に示すゲイン特性曲線から伝達関数\( \ G \left( s\right) \ \)を求めよ。ただし,\( \ \displaystyle G\left( s\right) =\frac {1}{T_{\mathrm {I1}}s} \ \)とおいて,その周波数伝達関数\( \ \displaystyle G\left( \mathrm {j}\omega \right) =\frac {1}{\mathrm {j}T_{\mathrm {I1}}\omega } \ \)のゲインが\( \ \omega = 0.1 \ \mathrm {rad / s} \ \)のとき\( \ 40 \ \mathrm {dB} \ \)であることを用いて\( \ T_{\mathrm {I1}} \ \)を決定せよ。
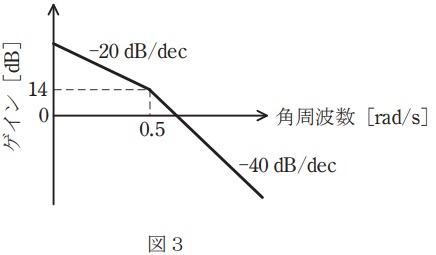
(4) 折れ線近似で表した図3に示すゲイン特性曲線から伝達関数\( \ G \left( s\right) \ \)を求めよ。ただし,\( \ G \left( s\right) \ \)を積分要素\( \ \displaystyle G_{1}\left( s\right) =\frac {1}{T_{\mathrm {I2}}s} \ \)と一次遅れ要素\( \ \displaystyle G_{2}\left( s\right) =\frac {1}{1+Ts} \ \)に分解して考えよ。
【ワンポイント解説】
ゲイン特性曲線から伝達関数を求める問題です。
伝達関数からゲイン特性曲線を描く問題は出題されたことがありますが,逆のパターンはあまり出題されたことがないので,選択した受験生は少なかったと予想されます。
しかしながら,慣れてしまえば比較的解きやすい内容となりますので,この問題で理解するようにしましょう。
1.ボード線図
周波数伝達関数が\( \ \displaystyle W(\mathrm {j}\omega ) =\frac {K}{1+\mathrm {j}\omega T} \ \)で与えられる時,ゲイン\( \ g \ \mathrm {[dB]} \ \)は,
\[
\begin{eqnarray}
g&=&20\log _{10} \left| W(\mathrm {j}\omega )\right| \\[ 5pt ]
&=&20\log _{10} \frac {K}{\sqrt {1+\left( \omega T\right) ^{2}}} \ \mathrm {[dB]} \\[ 5pt ]
\end{eqnarray}
\]
となりますが,\( \ \displaystyle \omega \ll \frac {1}{T} \ \)すなわち\( \ \omega T \ll 1 \ \)のとき,
\[
\begin{eqnarray}
g&≃&20\log _{10} \frac {K}{\sqrt {1+0}} \\[ 5pt ]
&=&20\log _{10}K \\[ 5pt ]
\end{eqnarray}
\]
とほぼ一定の値となり,\( \ \displaystyle \omega \gg \frac {1}{T} \ \)すなわち\( \ \omega T \gg 1 \ \)のとき,
\[
\begin{eqnarray}
g&≃&20\log _{10} \frac {K}{\sqrt {\left( \omega T\right) ^{2}}} \\[ 5pt ]
&=&20\log _{10} \frac {K}{\omega T} \\[ 5pt ]
&=&20\log _{10} K-20\log _{10}\omega T \\[ 5pt ]
\end{eqnarray}
\]
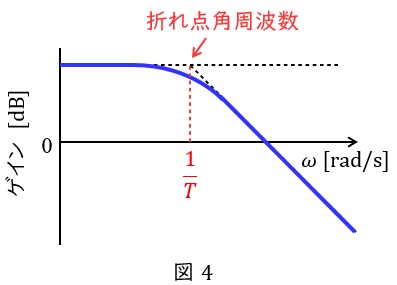
となり,横軸に対数座標をとると,ほぼ直線的に減少していくことになります。したがって,ボード線図は図4のようになります。
図4において\( \ \displaystyle \omega =\frac {1}{T} \ \)となる角周波数を折れ点角周波数と呼びます。
【解答】
(1)積分要素の伝達関数\( \ \displaystyle G_{1}\left( s\right) =\frac {1}{T_{\mathrm {I}}s} \ \)
求める積分要素の周波数伝達関数を\( \ \displaystyle G_{1}\left( \mathrm {j}\omega \right) =\frac {1}{\mathrm {j}\omega T_{\mathrm {I}}} \ \)とおくと,ゲイン\( \ g_{1} \ \mathrm {[dB]} \ \)は,ワンポイント解説「1.ボード線図」の通り,
\[
\begin{eqnarray}
g_{1}&=&20\log _{10} \left| G_{1}\left( \mathrm {j}\omega \right) \right| \\[ 5pt ]
&=&20\log _{10}\frac {1}{\omega T_{\mathrm {I}}} \\[ 5pt ]
&=&-20\log _{10} \omega T_{\mathrm {I}} \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,図1より,\( \ \omega =0.01 \ \mathrm {[rad / s]} \ \)のとき\( \ g_{1}=20 \ \mathrm {[dB]} \ \)であるから,
\[
\begin{eqnarray}
20&=&-20\log _{10} 0.01 T_{\mathrm {I}} \\[ 5pt ]
\log _{10} 0.01 T_{\mathrm {I}}&=&-1 \\[ 5pt ]
0.01 T_{\mathrm {I}}&=&0.1 \\[ 5pt ]
T_{\mathrm {I}}&=&10 \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
G_{1}\left( s\right) &=&\frac {1}{10s} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)\( \ G \left( s\right) =G_{1} \left( s\right) G_{2} \left( s\right) \ \)のように分解して\( \ G_{1} \left( s\right) \ \)を小問(1)で求めた伝達関数とするときの\( \ G_{2} \left( s\right) \ \)
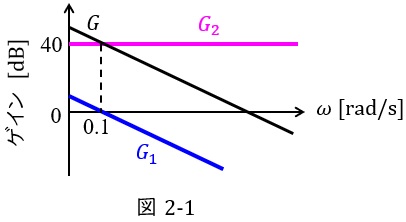
図2のゲイン特性曲線を図1の\( \ G_{1} \left( s\right) \ \)と\( \ G_{2} \left( s\right) \ \)に分解すると,図2-1のようになる。
したがって,周波数伝達関数\( \ G_{2} \left( \mathrm {j}\omega \right) \ \)のゲイン\( \ g_{2}=40 \ \mathrm {[dB]} \ \)であるから,
\[
\begin{eqnarray}
g_{2}&=&20\log _{10} \left| G_{2} \left( \mathrm {j}\omega \right) \right| \\[ 5pt ]
40&=&20\log _{10} \left| G_{2} \left( \mathrm {j}\omega \right) \right| \\[ 5pt ]
\log _{10} \left| G_{2} \left( \mathrm {j}\omega \right) \right| &=&2 \\[ 5pt ]
G_{2} \left( \mathrm {j}\omega \right) &=&100 \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ G_{2} \left( s\right) =100 \ \)と求められる。
(3)図2に示すゲイン特性曲線から伝達関数\( \ G \left( s\right) \ \)
(1)と同様に,求める積分要素の周波数伝達関数を\( \ \displaystyle G\left( \mathrm {j}\omega \right) =\frac {1}{\mathrm {j}\omega T_{\mathrm {I1}}} \ \)とおくと,ゲイン\( \ g \ \mathrm {[dB]} \ \)は,
\[
\begin{eqnarray}
g&=&-20\log _{10} \omega T_{\mathrm {I1}} \\[ 5pt ]
\end{eqnarray}
\]
となり,図2より,\( \ \omega =0.1 \ \mathrm {[rad / s]} \ \)のとき\( \ g=40 \ \mathrm {[dB]} \ \)であるから,
\[
\begin{eqnarray}
40&=&-20\log _{10} 0.1 T_{\mathrm {I1}} \\[ 5pt ]
\log _{10} 0.1 T_{\mathrm {I1}}&=&-2 \\[ 5pt ]
0.1 T_{\mathrm {I1}}&=&0.01 \\[ 5pt ]
T_{\mathrm {I1}}&=&0.1 \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
G \left( s\right) &=&\frac {1}{0.1s} \\[ 5pt ]
&=&\frac {10}{s} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)図3に示すゲイン特性曲線から伝達関数\( \ G \left( s\right) \ \)
題意の通り,\( \ G \left( s\right) \ \)を積分要素\( \ \displaystyle G_{1}\left( s\right) =\frac {1}{T_{\mathrm {I2}}s} \ \)と一次遅れ要素\( \ \displaystyle G_{2}\left( s\right) =\frac {1}{1+Ts} \ \)に分解し,\( \ \displaystyle G_{1}\left( s\right) =\frac {1}{T_{\mathrm {I2}}s} \ \)の周波数伝達関数を\( \ \displaystyle G_{1}\left( \mathrm {j}\omega \right) =\frac {1}{\mathrm {j}\omega T_{\mathrm {I2}}} \ \)とおくと,ゲイン\( \ g_{1} \ \mathrm {[dB]} \ \)は,(1)及び(3)と同様に,
\[
\begin{eqnarray}
g_{1}&=&-20\log _{10} \omega T_{\mathrm {I2}} \\[ 5pt ]
\end{eqnarray}
\]
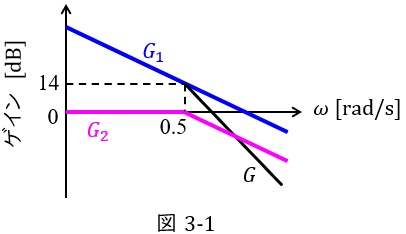
となる。それぞれのゲイン特性を示すと図3-1のようになる。図3-1より,\( \ \omega =0.5 \ \mathrm {[rad / s]} \ \)のとき\( \ g_{1}=14 \ \mathrm {[dB]} \ \)であるから,\( \ 14=20 \log _{10} 10^{0.7} \ \)及び\( \ 10^{0.7}=5.0119 \ \)に注意すると,
\[
\begin{eqnarray}
14&=&-20\log _{10} 0.5 T_{\mathrm {I2}} \\[ 5pt ]
20 \log _{10} 10^{0.7}&=&-20\log _{10} 0.5 T_{\mathrm {I2}} \\[ 5pt ]
\log _{10} 10^{0.7}&=&-\log _{10} 0.5 T_{\mathrm {I2}} \\[ 5pt ]
&=&\log _{10} \left( 0.5 T_{\mathrm {I2}}\right) ^{-1} \\[ 5pt ]
&=&\log _{10} \frac {2}{T_{\mathrm {I2}}} \\[ 5pt ]
10^{0.7}&=& \frac {2}{T_{\mathrm {I2}}} \\[ 5pt ]
5.0119&=& \frac {2}{T_{\mathrm {I2}}} \\[ 5pt ]
T_{\mathrm {I2}}&=& \frac {2}{5.0119} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
G_{1}\left( s\right) &=&\frac {5.0119}{2s} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。同様に,一次遅れ要素\( \ \displaystyle G_{2}\left( s\right) =\frac {1}{1+Ts} \ \)の周波数伝達関数を\( \ \displaystyle G_{2}\left( \mathrm {j}\omega \right) =\frac {1}{1+\mathrm {j}\omega T} \ \)とおくと,ゲイン\( \ g_{2} \ \mathrm {[dB]} \ \)は,ワンポイント解説「1.ボード線図」の通り,
\[
\begin{eqnarray}
g_{2}&=&20\log _{10} \left| G_{2}\left( \mathrm {j}\omega \right) \right| \\[ 5pt ]
&=&20\log _{10}\frac {1}{\sqrt {1+\left( \omega T\right) ^{2}}} \\[ 5pt ]
&=&-20\log _{10} \sqrt {1+\left( \omega T\right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,\( \ \displaystyle \omega \gg \frac {1}{T} \ \)すなわち\( \ \omega T \gg 1 \ \)であるとすると,
\[
\begin{eqnarray}
g_{2}&≃&-20\log _{10} \sqrt {\left( \omega T\right) ^{2}} \\[ 5pt ]
&=&-20\log _{10} \omega T \\[ 5pt ]
\end{eqnarray}
\]
となり,図3-1の折れ線近似により,\( \ \omega =0.5 \ \mathrm {[rad / s]} \ \)のとき\( \ g_{2}=0 \ \mathrm {[dB]} \ \)であるから,
\[
\begin{eqnarray}
0&=&-20\log _{10} 0.5T \\[ 5pt ]
\log _{10} 0.5T&=&0 \\[ 5pt ]
0.5T&=&1 \\[ 5pt ]
T&=&2 \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
G_{2}\left( s\right) &=&\frac {1}{1+2s} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。以上から,求める伝達関数\( \ G \left( s\right) \ \)は,
\[
\begin{eqnarray}
G\left( s\right) &=&G_{1}\left( s\right) G_{2}\left( s\right) \\[ 5pt ]
&=&\frac {5.0119}{2s}\cdot \frac {1}{1+2s} \\[ 5pt ]
&≒&\frac {5.01}{2s\left( 1+2s\right) } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは