《機械・制御》〈同期機〉[R07:問1]三相円筒形同期電動機及び同期調相機に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

三相円筒形同期電動機を遅れ力率で運転する場合に関して，次の問に答えよ。ただし，単位法の基準は電動機の定格容量及び定格電圧とし，電動機の損失は無視するものとする。

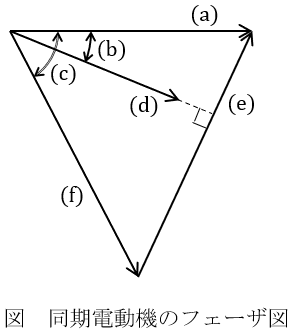
(1)　この電動機の同期リアクタンスを\( \ X_{\mathrm {s}} \ \mathrm {[p.u.]} \ \)，端子電圧（相電圧）を\( \ V \ \mathrm {[p.u.]} \ \)，無負荷誘導起電力を\( \ E \ \mathrm {[p.u.]} \ \)，電機子電流を\( \ I \ \mathrm {[p.u.]} \ \)，力率角を\( \ \theta \ \mathrm {[rad]} \ \)，負荷角を\( \ \delta \ \mathrm {[rad]} \ \)として，そのフェーザ図は次ページの図のようになった。このフェーザ図中の\( \ \mathrm {(a)} \ \)，\( \ \mathrm {(b)} \ \)，\( \ \mathrm {(c)} \ \)，\( \ \mathrm {(d)} \ \)，\( \ \mathrm {(e)} \ \)，\( \ \mathrm {(f)} \ \)に当てはまる記号を答えよ。（解答例\( \ \mathrm {(a)}\dot I \ \)，\( \ \mathrm {(b)}\dot V \ \)，\( \ \mathrm {(c)}\mathrm {j}X_{\mathrm {s}}\dot I \ \)，\( \ \cdots \ \)）

(2)　フェーザ図から\( \ E \ \)を，\( \ V \ \)，\( \ \theta \ \)，\( \ I \ \)，\( \ X_{\mathrm {s}} \ \)で表す式を導出せよ。

(3)　小問(2)で求めた式から，電動機が定格力率\( \ =0.8 \ \)，\( \ X_{\mathrm {s}}=2.0 \ \mathrm {p.u.} \ \)である場合の定格運転時の\( \ E \ \)の値を求めよ。

(4)　フェーザ図から\( \ X_{\mathrm {s}}I \ \)を\( \ E \ \)，\( \ V \ \)，及び\( \ \cos \delta \ \)で表す式を導出せよ。

(5)　この電動機を同期調相機として運転する場合に次の問に答えよ。ただし，このときの端子電圧は定格電圧一定とする。

　\( \ \mathrm {a)} \ \)　小問(4)で求めた式から，\( \ I \ \)を\( \ E \ \)と\( \ X_{\mathrm {s}} \ \)で表す式を求めよ。

　\( \ \mathrm {b)} \ \)　小問(5)\( \ \mathrm {a)} \ \)で求めた式は，界磁電流を調整して\( \ E \ \)を変化させたときの\( \ I \ \)の値を示すグラフを表し，これは同期調相機の\( \ \mathrm {V} \ \)曲線に相当する。このグラフにおいて，\( \ I \ \)が最小値のときの\( \ E \ \)の値を求めよ。

【ワンポイント解説】

三相円筒形同期電動機の諸計算に関する問題です。
フェーザ図をしっかりと扱える幾何学的な能力が求められています。
同期電動機及び同期調相機のメカニズムを理解するためにはとても良い問題です。

1.三相同期電動機の等価回路及びベクトル図
三相同期電動機の等価回路は，端子電圧\( \ \dot V \ \mathrm {[V]} \ \)（相電圧），誘導起電力\( \ \dot E \ \mathrm {[V]} \ \)（相電圧），電機子電流\( \ \dot I \ \mathrm {[A]} \ \)，同期リアクタンス\( \ x_{\mathrm {s}} \ \mathrm {[\Omega ]} \ \)とすると，図1のようになります。ただし，電機子巻線抵抗は十分に小さいものとします。

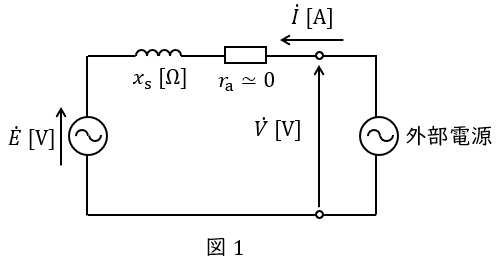
等価回路にキルヒホッフの法則を適用すると，
\[
\begin{eqnarray}
\dot V &=& \dot E+\mathrm {j}x_{\mathrm {s}}\dot I \\[ 5pt ] \end{eqnarray}
\] の関係があることがわかります。
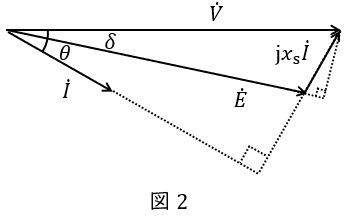
これより，\( \ \dot V \ \mathrm {[V]} \ \)と\( \ \dot I \ \mathrm {[A]} \ \)の力率角を\( \ \theta \ \mathrm {[rad]} \ \)，\( \ \dot V \ \mathrm {[V]} \ \)と\( \ \dot E \ \mathrm {[V]} \ \)の負荷角を\( \ \delta \ \mathrm {[rad]} \ \)とすると，ベクトル図は図2のように描くことができます。

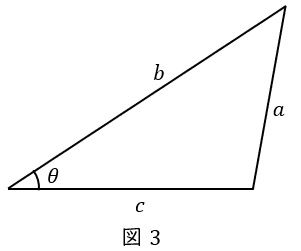
3.余弦定理
図3に示すような三角形（任意の三角形）において，
\[
\begin{eqnarray}
a^{2}&=&b^{2}+c^{2}-2bc\cos \theta \\[ 5pt ] \end{eqnarray}
\] の関係が成立し，これを余弦定理といいます。

【解答】

(1)フェーザ図中の\( \ \mathrm {(a)} \ \)，\( \ \mathrm {(b)} \ \)，\( \ \mathrm {(c)} \ \)，\( \ \mathrm {(d)} \ \)，\( \ \mathrm {(e)} \ \)，\( \ \mathrm {(f)} \ \)に当てはまる記号
ワンポイント解説「1.三相同期電動機の等価回路及びベクトル図」の通り，
\[
\begin{eqnarray}
\mathrm {(a)}&:&\dot V \\[ 5pt ] \mathrm {(b)}&:&\theta \\[ 5pt ] \mathrm {(c)}&:&\delta \\[ 5pt ] \mathrm {(d)}&:&\dot I \\[ 5pt ] \mathrm {(e)}&:&\mathrm {j}X_{\mathrm {s}}\dot I \\[ 5pt ] \mathrm {(f)}&:&\dot E \\[ 5pt ] \end{eqnarray}
\] となる。

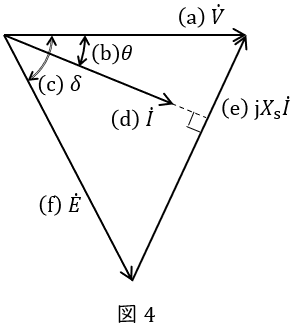
(2)\( \ E \ \)を，\( \ V \ \)，\( \ \theta \ \)，\( \ I \ \)，\( \ X_{\mathrm {s}} \ \)で表す式
フェーザ図において，図5に示す三角形に三平方の定理を適用すると，
\[
\begin{eqnarray}
E &=&\sqrt {\left( V\cos \theta \right) ^{2} +\left( X_{\mathrm {s}}I-V\sin \theta \right) ^{2} } \\[ 5pt ] &=&\sqrt { V^{2}\cos ^{2}\theta +\left( X_{\mathrm {s}}I\right) ^{2} -2VX_{\mathrm {s}}I\sin \theta +V^{2}\sin ^{2}\theta } \\[ 5pt ] &=&\sqrt { V^{2} +\left( X_{\mathrm {s}}I\right) ^{2} -2VX_{\mathrm {s}}I\sin \theta } \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)電動機が定格力率\( \ =0.8 \ \)，\( \ X_{\mathrm {s}}=2.0 \ \mathrm {p.u.} \ \)である場合の定格運転時の\( \ E \ \)の値
\( \ \cos \theta =0.8 \ \)より\( \ \sin \theta \ \)は，
\[
\begin{eqnarray}
\sin \theta &=&\sqrt {1-\cos ^{2}\theta } \\[ 5pt ] &=&\sqrt {1-0.8 ^{2}} \\[ 5pt ] &=&0.6 \\[ 5pt ] \end{eqnarray}
\] となり，定格運転時なので，(2)解答式にこれと\( \ V=1.0 \ \mathrm {[p.u.]} \ \)，\( \ I=1.0 \ \mathrm {[p.u.]} \ \)，\( \ X_{\mathrm {s}}=2.0 \ \mathrm {[p.u.]} \ \)を代入すると，
\[
\begin{eqnarray}
E &=&\sqrt { V^{2} +\left( X_{\mathrm {s}}I\right) ^{2} -2VX_{\mathrm {s}}I\sin \theta } \\[ 5pt ] &=&\sqrt { 1.0^{2} +\left( 2.0\times 1.0\right) ^{2} -2\times 1.0\times 2.0\times 1.0\times 0.6 } \\[ 5pt ] &=&\sqrt { 2.6 } \\[ 5pt ] &≒&1.612 \ 5　→　1.61 \ \mathrm {[p.u.]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

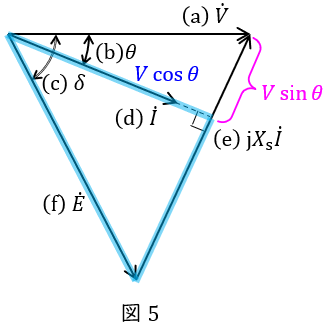
(4)\( \ X_{\mathrm {s}}I \ \)を\( \ E \ \)，\( \ V \ \)，及び\( \ \cos \delta \ \)で表す式
図6に示す三角形に余弦定理を適用すると，
\[
\begin{eqnarray}
\left( X_{\mathrm {s}}I\right) ^{2} &=&V^{2}+E^{2}-2VE\cos \delta \\[ 5pt ] X_{\mathrm {s}}I&=&\sqrt {V^{2}+E^{2}-2VE\cos \delta } \\[ 5pt ] \end{eqnarray}
\] と求められる。

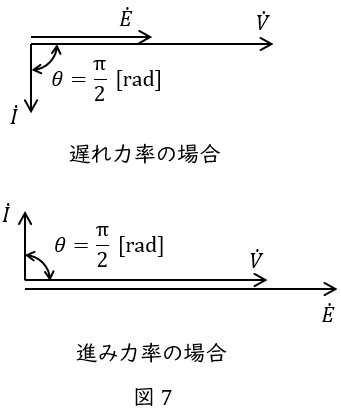
(5)\( \ \mathrm {a)} \ \)同期調相機として運転する場合，\( \ I \ \)を\( \ E \ \)と\( \ X_{\mathrm {s}} \ \)で表す式
同期調相機は無負荷の同期電動機なので，運転時のフェーザ図は図7に示すようになる。したがって，同期調相機の負荷角\( \ \delta =0 \ \mathrm {[rad]} \ \)であり，\( \ \cos \delta =1 \ \)となるので，これと\( \ V=1.0 \ \mathrm {[p.u.]} \ \)を(4)解答式に代入すると，
\[
\begin{eqnarray}
X_{\mathrm {s}}I&=&\sqrt {V^{2}+E^{2}-2VE\cos \delta } \\[ 5pt ] &=&\sqrt {1.0^{2}+E^{2}-2\times 1.0 \times E\times 1.0 } \\[ 5pt ] &=&\sqrt {E^{2}-2E+1} \\[ 5pt ] &=&\sqrt {\left( E-1\right) ^{2}} \\[ 5pt ] &=&\left| E-1\right| \\[ 5pt ] I&=&\frac {\left| E-1\right| }{X_{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

\( \ \mathrm {b)} \ \)\( \ V \ \)曲線において，\( \ I \ \)が最小値のときの\( \ E \ \)の値
(5)\( \ \mathrm {a)} \ \)解答式において，\( \ I \ \)の最小値は\( \ 0 \ \)なので，
\[
\begin{eqnarray}
0&=&\frac {\left| E-1\right| }{X_{\mathrm {s}}} \\[ 5pt ] \left| E-1\right|&=&0 \\[ 5pt ] E&=&1 \ \mathrm {[p.u.]} \\[ 5pt ] \end{eqnarray}
\] と求められる。