Contents
【問題】
【難易度】★★☆☆☆(やや易しい)
図はフィードバック制御系の基本構成を示し,\( \ G_{\mathrm {c}} (s) \ \)は補償器の伝達関数,\( \ G_{\mathrm {p}} (s) \ \)は制御対象の伝達関数を表わしている。また,\( \ R (s) \ \),\( \ E (s) \ \),\( \ Y (s) \ \)は,目標信号\( \ r (t) \ \),偏差信号\( \ e (t) \ \),制御量\( \ y (t) \ \)をそれぞれラプラス変換したものである。
\( \ \displaystyle G_{\mathrm {c}} (s)=\frac {2s+4}{s} \ \),\( \ \displaystyle G_{\mathrm {p}} (s)=\frac {1}{s+3} \ \)として,次の問に答えよ。
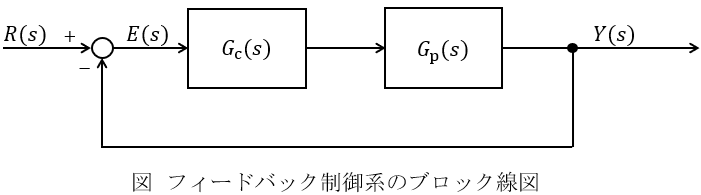
(1) \( \ R (s) \ \)から\( \ E (s) \ \)までの伝達関数\( \ G_{\mathrm {e}} (s) \ \)を求めよ。
(2) 目標信号として大きさ\( \ a \ \)のステップ信号,\( \ \begin{eqnarray}
r (t) =
\begin{cases}
0 & ( t \lt 0 ) \\
a & ( t ≧ 0 )
\end{cases}
\end{eqnarray} \ \)を入力したときの定常偏差を求めよ。
(3) 目標信号として傾き\( \ b \ \)のランプ信号,\( \ \begin{eqnarray}
r (t) =
\begin{cases}
0 & ( t \lt 0 ) \\
bt & ( t ≧ 0 )
\end{cases}
\end{eqnarray} \ \)を入力したときの定常偏差を求めよ。
(4) \( \ R (s) \ \)から\( \ Y (s) \ \)までの伝達関数\( \ G_{\mathrm {y}} (s) \ \)を求め,\( \ G_{\mathrm {y}} (s) \ \)のインパルス応答\( \ g_{\mathrm {y}} (t) \ \),\( \ t \gt 0 \ \)を求めよ。
(5) 目標信号として\( \ \begin{eqnarray}
r (t) =
\begin{cases}
0 & ( t \lt 0 ) \\
1 & ( t ≧ 0 )
\end{cases}
\end{eqnarray} \ \)を入力したとき,時刻\( \ t=1 \ \)の制御量\( \ y (1) \ \)を求めよ。なお,自然対数の底\( \ \mathrm {e} \ \)に対して\( \ \mathrm {e}^{-1}=3.679\times 10^{-1} \ \)とする。
【ワンポイント解説】
フィードバック制御系の信号応答に関する問題です。
考え方はラプラス変換の基本なので易しいですが,途中で高い計算力が求められる問題です。
計算が得意な方は選択すると良い問題かと思います。
1.基本的なラプラス変換
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると以下のような関係があります。
\[
\begin{array}{|c|c|}
\hline
f(t) & F(s) \\
\hline
{\displaystyle \delta (t) }\atop{単位インパルス関数} & 1 \\[ 5pt ]
{\displaystyle u (t) }\atop{単位ステップ関数} & \displaystyle \frac {1}{s} \\[ 5pt ]
K & \displaystyle \frac {K}{s} \\[ 5pt ]
t & \displaystyle \frac {1}{s^{2}} \\[ 5pt ]
\mathrm {e}^{at} & \displaystyle \frac {1}{s-a} \\[ 5pt ]
\sin \omega t & \displaystyle \frac {\omega }{s^{2}+\omega ^{2}} \\[ 5pt ]
\cos \omega t & \displaystyle \frac {s}{s^{2}+\omega ^{2}} \\[ 5pt ]
\displaystyle \frac {\mathrm {d}f\left( t \right) }{\mathrm {d}t} & sF\left( s \right) -f\left( 0 \right) \\[ 5pt ]
\displaystyle \int f\left( t \right) \mathrm {d}t & \displaystyle \frac {F\left( s \right) }{s}+\frac {1}{s}\int _{-\infty }^{0}f\left( \tau \right) \mathrm {d}\tau \\[ 5pt ]
\hline
\end{array}
\]
2.ブロック線図の考え方
①直列
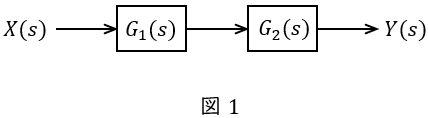
図1のような伝達関数\( \ G_{1}(s) \ \),\( \ G_{2}(s) \ \)が与えられているとき,全体の伝達関数\( \ G(s) \ \)は,
\[
\begin{eqnarray}
G(s)&=&\frac {Y(s)}{X(s)}=G_{1}(s)G_{2}(s) \\[ 5pt ]
\end{eqnarray}
\]
となります。
②並列
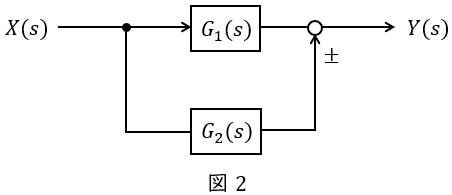
図2のような伝達関数\( \ G_{1}(s) \ \),\( \ G_{2}(s) \ \)が与えられているとき,全体の伝達関数\( \ G(s) \ \)は,
\[
\begin{eqnarray}
G(s)&=&\frac {Y(s)}{X(s)}=G_{1}(s)±G_{2}(s) \\[ 5pt ]
\end{eqnarray}
\]
となります。
③フィードバック
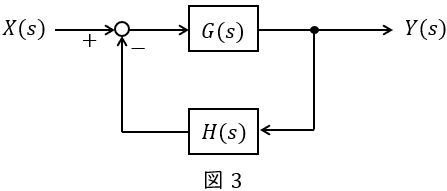
図3のような\( \ G(s) \ \),\( \ H(s) \ \)が与えられているとき,全体の伝達関数\( \ W(s) \ \)は,
\[
\begin{eqnarray}
Y(s)&=&\left\{ X(s) -H(s)Y(s) \right\} G(s) \\[ 5pt ]
Y(s)&=&G(s)X(s) -G(s)H(s)Y(s) \\[ 5pt ]
Y(s)+G(s)H(s)Y(s) &=&G(s)X(s) \\[ 5pt ]
\left\{ 1+G(s)H(s)\right\} Y(s) &=&G(s)X(s) \\[ 5pt ]
\frac {Y(s)}{X(s)}&=&\frac {G(s)}{1+G(s)H(s)} \\[ 5pt ]
W(s)&=&\frac {G(s)}{1+G(s)H(s)} \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.最終値の定理
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると,\( \ f(t) \ \)の定常値は,
\[
\begin{eqnarray}
\displaystyle \lim _{ t \to \infty } f(t)&=&\displaystyle \lim _{ s \to 0 } sF(s) \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
【解答】
(1)\( \ R (s) \ \)から\( \ E (s) \ \)までの伝達関数\( \ G_{\mathrm {e}} (s) \ \)
問題図より,\( \ R (s) \ \)から\( \ E (s) \ \)までの関係式は,ワンポイント解説「2.ブロック線図の考え方」の通り,
\[
\begin{eqnarray}
R (s)-E (s)G_{\mathrm {c}} (s)G_{\mathrm {p}} (s) &=&E (s) \\[ 5pt ]
\end{eqnarray}
\]
となるため,これを整理すると伝達関数\( \ G_{\mathrm {e}} (s) \ \)は,
\[
\begin{eqnarray}
R (s)&=&E (s)+E (s)G_{\mathrm {c}} (s)G_{\mathrm {p}} (s) \\[ 5pt ]
R (s)&=&\left\{ 1+G_{\mathrm {c}} (s)G_{\mathrm {p}} (s) \right\} E (s) \\[ 5pt ]
\frac {E (s)}{R (s)}&=&\frac {1}{1+G_{\mathrm {c}} (s)G_{\mathrm {p}} (s)} \\[ 5pt ]
G_{\mathrm {e}} (s)&=&\frac {1}{\displaystyle 1+\frac {2s+4}{s}\cdot \frac {1}{s+3}} \\[ 5pt ]
&=&\frac {1}{\displaystyle \frac {s\left( s+3\right) +2s+4}{s\left( s+3\right) }} \\[ 5pt ]
&=&\frac {s\left( s+3\right) }{s\left( s+3\right) +2s+4} \\[ 5pt ]
&=&\frac {s^{2}+3s }{s^{2}+5s+4} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)大きさ\( \ a \ \)のステップ信号を入力したときの定常偏差
\( \ r(t)=a \ \)のラプラス変換\( \ R(s) \ \)は,ワンポイント解説「1.基本的なラプラス変換」の通り,
\[
\begin{eqnarray}
R (s)&=&\frac {a}{s} \\[ 5pt ]
\end{eqnarray}
\]
となるので,大きさ\( \ a \ \)のステップ信号を入力したときの定常偏差は,ワンポイント解説「3.最終値の定理」の通り,
\[
\begin{eqnarray}
\displaystyle \lim _{ t \to \infty } e(t)&=&\displaystyle \lim _{ s \to 0 } sE(s) \\[ 5pt ]
&=&\displaystyle \lim _{ s \to 0 } sG_{\mathrm {e}} (s)R(s) \\[ 5pt ]
&=&\displaystyle \lim _{ s \to 0 } s\cdot \frac {s^{2}+3s }{s^{2}+5s+4}\cdot \frac {a}{s} \\[ 5pt ]
&=&\displaystyle \lim _{ s \to 0 } \frac { s^{2}+3s }{s^{2}+5s+4}\cdot a \\[ 5pt ]
&=&0 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)傾き\( \ b \ \)のランプ信号を入力したときの定常偏差
\( \ r(t)=bt \ \)のラプラス変換\( \ R(s) \ \)は,ワンポイント解説「1.基本的なラプラス変換」の通り,
\[
\begin{eqnarray}
R (s)&=&\frac {b}{s^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,傾き\( \ b \ \)のランプ信号を入力したときの定常偏差は,ワンポイント解説「3.最終値の定理」の通り,
\[
\begin{eqnarray}
\displaystyle \lim _{ t \to \infty } e(t)&=&\displaystyle \lim _{ s \to 0 } sE(s) \\[ 5pt ]
&=&\displaystyle \lim _{ s \to 0 } sG_{\mathrm {e}} (s)R(s) \\[ 5pt ]
&=&\displaystyle \lim _{ s \to 0 } s\cdot \frac {s^{2}+3s }{s^{2}+5s+4}\cdot \frac {b}{s^{2}} \\[ 5pt ]
&=&\displaystyle \lim _{ s \to 0 } \frac {s+3 }{s^{2}+5s+4}\cdot b \\[ 5pt ]
&=&\frac {3}{4}b \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)\( \ R (s) \ \)から\( \ Y (s) \ \)までの伝達関数\( \ G_{\mathrm {y}} (s) \ \),\( \ G_{\mathrm {y}} (s) \ \)のインパルス応答\( \ g_{\mathrm {y}} (t) \ \)
\( \ R (s) \ \)から\( \ Y (s) \ \)までの伝達関数\( \ G_{\mathrm {y}} (s) \ \)は,ワンポイント解説「2.ブロック線図の考え方」の通り,
\[
\begin{eqnarray}
G_{\mathrm {y}} (s)&=&\frac {G_{\mathrm {c}} (s)G_{\mathrm {p}} (s)}{1+G_{\mathrm {c}} (s)G_{\mathrm {p}} (s)} \\[ 5pt ]
&=&\frac {\displaystyle \frac {2s+4}{s}\cdot \frac {1}{s+3}}{\displaystyle 1+\frac {2s+4}{s}\cdot \frac {1}{s+3}} \\[ 5pt ]
&=&\frac {\displaystyle \frac {2s+4}{s\left( s+3\right) }}{\displaystyle \frac {s\left( s+3\right) +2s+4}{s\left( s+3\right) }} \\[ 5pt ]
&=&\frac {2s+4}{s\left( s+3\right) +2s+4} \\[ 5pt ]
&=&\frac {2s+4}{s^{2}+5s+4} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。次に,インパルス応答のラプラス変換は\( \ 1 \ \)なので,インパルス応答は\( \ G_{\mathrm {y}} (s) \ \)を時間関数に逆ラプラス変換すればよい。ここで,\( \ \displaystyle G_{\mathrm {y}} (s)=\frac {2s+4}{s^{2}+5s+4}=\frac {A}{s+1}+\frac {B}{s+4} \ \)とおけば,
\[
\begin{eqnarray}
\frac {A}{s+1}+\frac {B}{s+4}&=&\frac {A\left( s+4\right) +B\left( s+1\right) }{\left( s+1\right) \left( s+4\right) } \\[ 5pt ]
&=&\frac {\left( A+B\right) s+\left( 4A+B\right) }{s^{2}+5s+4} \\[ 5pt ]
\end{eqnarray}
\]
となるので,係数比較をすれば,
\[
\begin{eqnarray}
\left\{
\begin{array}{l}
A+B &=& 2 ・・・・・・・・・ ① \\
4A+B &=& 4 ・・・・・・・・・ ② \\
\end{array}
\right.
\end{eqnarray}
\]
となる。\( \ ②-① \ \)より,
\[
\begin{eqnarray}
3A&=&2 \\[ 5pt ]
A&=&\frac {2}{3} \\[ 5pt ]
\end{eqnarray}
\]
となり,これを\( \ ① \ \)に代入すると,
\[
\begin{eqnarray}
\frac {2}{3}+B &=& 2 \\[ 5pt ]
B&=&\frac {4}{3} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ \displaystyle G_{\mathrm {y}} (s) =\frac {2}{3}\frac {1}{s+1}+\frac {4}{3}\frac {1}{s+4} \ \)となるから,これを逆ラプラス変換すると\( \ g_{\mathrm {y}} (t) \ \)は,ワンポイント解説「1.基本的なラプラス変換」の通り,
\[
\begin{eqnarray}
g_{\mathrm {y}} (t) &=& \frac {2}{3}\mathrm {e}^{-t}+\frac {4}{3}\mathrm {e}^{-4t} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)\( \ \begin{eqnarray}
r (t) =
\begin{cases}
0 & ( t \lt 0 ) \\
1 & ( t ≧ 0 )
\end{cases}
\end{eqnarray} \ \)を入力したときの時刻\( \ t=1 \ \)の制御量\( \ y (1) \ \)
\( \ r(t)=1 \ \)のラプラス変換\( \ R(s) \ \)は,ワンポイント解説「1.基本的なラプラス変換」の通り,
\[
\begin{eqnarray}
R (s)&=&\frac {1}{s} \\[ 5pt ]
\end{eqnarray}
\]
となるので\( \ Y (s) \ \)は,
\[
\begin{eqnarray}
Y (s)&=&G_{\mathrm {y}} (s)R (s) \\[ 5pt ]
&=&\frac {2s+4}{s^{2}+5s+4}\frac {1}{s} \\[ 5pt ]
&=&\frac {2s+4}{s\left( s+1 \right) \left( s+4\right) } \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \displaystyle Y (s)=\frac {2s+4}{s\left( s+1 \right) \left( s+4\right) }=\frac {C}{s}+\frac {D}{s+1}+\frac {E}{s+4} \ \)とおけば,
\[
\begin{eqnarray}
\frac {C}{s}+\frac {D}{s+1}+\frac {E}{s+4}&=&\frac {C\left( s+1 \right) \left( s+4\right) +Ds\left( s+4\right) +Es\left( s+1\right) }{s\left( s+1\right) \left( s+4\right) } \\[ 5pt ]
&=&\frac {C\left( s^{2}+5s+4 \right) +D\left( s^{2}+4s\right) +E\left( s^{2}+s\right) }{s\left( s+1\right) \left( s+4\right) } \\[ 5pt ]
&=&\frac {\left( C+D+E \right) s^{2}+\left( 5C+4D+E\right) s+4C }{s\left( s+1\right) \left( s+4\right) } \\[ 5pt ]
\end{eqnarray}
\]
となるので,係数比較をすれば,
\[
\begin{eqnarray}
\left\{
\begin{array}{l}
C+D+E &=& 0 &・・・・・・・・・ ③& \\
5C+4D+E &=& 2 &・・・・・・・・・ ④& \\
4C &=& 4 &・・・・・・・・・ ⑤& \\
\end{array}
\right.
\end{eqnarray}
\]
となる。\( \ ⑤ \ \)より\( \ C=1 \ \)となるので,これを\( \ ③ \ \)及び\( \ ④ \ \)に代入して整理すると,
\[
\begin{eqnarray}
\left\{
\begin{array}{l}
D+E &=& -1 &・・・・・・・・・ ③^{\prime }& \\
4D+E &=& -3 &・・・・・・・・・ ④^{\prime }& \\
\end{array}
\right.
\end{eqnarray}
\]
となり,\( \ ④^{\prime }-③^{\prime } \ \)より,
\[
\begin{eqnarray}
3D&=&-2 \\[ 5pt ]
D&=&-\frac {2}{3} \\[ 5pt ]
\end{eqnarray}
\]
となる。これを\( \ ③^{\prime } \ \)に代入すると,
\[
\begin{eqnarray}
-\frac {2}{3}+E &=& -1 \\[ 5pt ]
E&=&-\frac {1}{3} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ \displaystyle Y (s)=\frac {1}{s}-\frac {2}{3}\frac {1}{s+1}-\frac {1}{3}\frac {1}{s+4} \ \)となるから,これを逆ラプラス変換すると\( \ y (t) \ \)は,ワンポイント解説「1.基本的なラプラス変換」の通り,
\[
\begin{eqnarray}
y (t) &=& 1-\frac {2}{3}\mathrm {e}^{-t}-\frac {1}{3}\mathrm {e}^{-4t} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,時刻\( \ t=1 \ \)の制御量\( \ y (1) \ \)は,
\[
\begin{eqnarray}
y (1)&=& 1-\frac {2}{3}\mathrm {e}^{-1}-\frac {1}{3}\mathrm {e}^{-4} \\[ 5pt ]
&=& 1-\frac {2}{3}\times 3.679 \times 10^{-1}-\frac {1}{3}\times \left( 3.679 \times 10^{-1}\right) ^{4} \\[ 5pt ]
&≒& 0.749 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは