Contents
【問題】
【難易度】★★★☆☆(普通)
次の文章は,接地抵抗の測定に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる式又は図を解答群の中から選び,その記号をマークシートに記入しなさい。
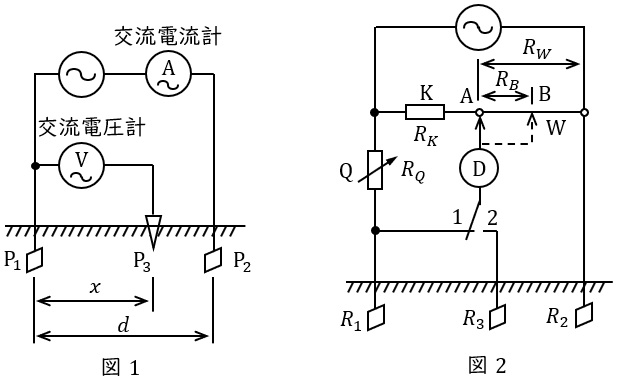
図1は接地抵抗の測定原理を示したものである。図1において,接地電極\( \ \mathrm {P}_{1} \ \)から距離\( \ d \ \)離れた所に補助電極\( \ \mathrm {P}_{2} \ \)を,距離\( \ x \ \)の所に補助電極\( \ \mathrm {P}_{3} \ \)を設け接地する。\( \ \mathrm {P}_{1} \ \)と\( \ \mathrm {P}_{2} \ \)間に交流電流を流し,\( \ \mathrm {P}_{3} \ \)を移動させて交流電圧計の読み,すなわち地表面の\( \ \mathrm {P}_{1} \ \)からの電位\( \ v \ \)を図に表すと,\( \ \fbox { (1) } \ \)のようになる。
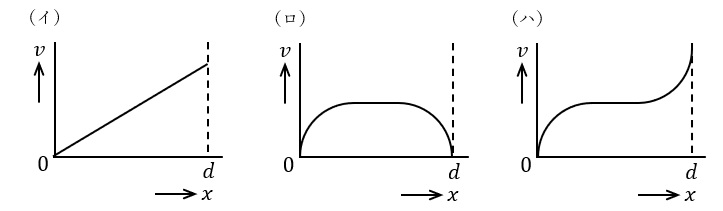
一方,図2において,\( \ R_{1} \ \)は求めようとする接地抵抗の値,\( \ R_{2} \ \)及び\( \ R_{3} \ \)は補助電極の抵抗値,\( \ \mathrm {K} \ \)は抵抗値\( \ R_{K} \ \)の固定抵抗器とする。また,\( \ \mathrm {Q} \ \)は半固定抵抗器,\( \ \mathrm {W} \ \)は抵抗値\( \ R_{W} \ \)の滑り線抵抗器である。
いま,検出器\( \ \Large{Ⓓ} \ \)の一端を滑り線抵抗器\( \ \mathrm {W} \ \)の\( \ \mathrm {A} \ \)点に接触させ,スイッチ\( \ \mathrm {S} \ \)を\( \ 1 \ \)側に閉じる。半固定抵抗器\( \ \mathrm {Q} \ \)を調整して,その抵抗値が\( \ R_{Q} \ \)のとき回路が平衡したとすれば,次式が得られる。
\[
\begin{eqnarray}
&\ \fbox { (2) } \ &・・・・・・・・・・・・ ①& \\[ 5pt ]
\end{eqnarray}
\]
次に,半固定抵抗器\( \ \mathrm {Q} \ \)の抵抗値\( \ R_{Q} \ \)はそのままの状態で,スイッチ\( \ \mathrm {S} \ \)を\( \ 2 \ \)側に閉じる。検出器の一端を滑り線抵抗器\( \ \mathrm {W} \ \)の\( \ \mathrm {B} \ \)点に移動させて回路の平衡が得られたとすると,次式が得られる。ただし,滑り線抵抗器\( \ \mathrm {W} \ \)の\( \ \mathrm {A} \ \)点から\( \ \mathrm {B} \ \)点までの抵抗値を\( \ R_{B} \ \)とする。
\[
\begin{eqnarray}
&\ \fbox { (3) } \ &・・・・・・・・・・・・ ②& \\[ 5pt ]
\end{eqnarray}
\]
①及び②式から\( \ R_{2} \ \)を消去して\( \ R_{1} \ \)を求めると,\( \ R_{1}= \ \fbox { (4) } \ \)となる。したがって,滑り線抵抗器\( \ \mathrm {W} \ \)を予め細かく目盛っておけば,その読みと\( \ \fbox { (5) } \ \)の値から\( \ R_{1} \ \)を求めることができる。
〔問6の解答群〕
\[
\begin{eqnarray}
&(ニ)& \left( R_{2}+R_{3}\right) \left( R_{K}+R_{B}\right) =\left( R_{Q}+R_{1}\right) \left( R_{W}-R_{B}\right) &(ホ)& R_{K}\left( R_{1}+R_{2}\right) =R_{Q}R_{W} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
&(ヘ)& \frac {\left( R_{K}+R_{B}\right) R_{Q}}{R_{W}} \ &(ト)& \frac {R_{Q}}{R_{K}} &(チ)& R_{K}R_{1} =R_{Q}\left( R_{W}+R_{2}\right) \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
&(リ)& \frac {R_{K}+R_{B}}{R_{W}} &(ヌ)& \left( R_{Q}+R_{1}\right) \left( R_{W}-R_{B}\right) =R_{2} \left( R_{K}+R_{B}\right) \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
&(ル)& \frac {R_{K}R_{Q}}{R_{B}} \ &(ヲ)& \frac {R_{K}}{R_{B}} &(ワ)& R_{K}R_{2} =R_{W}R_{1} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
&(カ)& \left( R_{Q}+R_{1}+R_{3}\right) \left( R_{W}-R_{B}\right) =R_{2} \left( R_{K}+R_{B}\right) \ &(ヨ)& \frac {R_{B}R_{Q}}{R_{K}} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
接地抵抗の測定原理から接地抵抗値を導出する問題です。
ブリッジ回路の平衡条件を利用して導出していくため,ブリッジ回路のどの部分がどの抵抗になるかよく考えて解いていく必要があります。
(4)の計算量が多いので,丁寧にミスのないように解いていく必要があります。
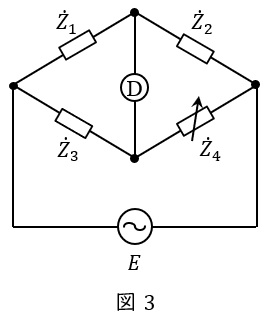
1.交流ブリッジ回路の平衡条件
図3の回路において,検流計Ⓓに電流が流れないようにしたとき,各インピーダンスの関係は,
\[
\begin{eqnarray}
{\dot Z}_{1}{\dot Z}_{4}&=&{\dot Z}_{2}{\dot Z}_{3} \\[ 5pt ]
\end{eqnarray}
\]
となります。これをブリッジの平衡条件といい,コンデンサの静電容量を求めるシェーリングブリッジ,電源の周波数を求めるウィーンブリッジ,コイルのインダクタンスを求めるヘイブリッジ,等様々な測定に利用されています。
【解答】
(1)解答:ハ
一般に電極近傍における電位は,電極からの距離に反比例した分布となるので,\( \ \mathrm {P_{1}} \ \)及び\( \ \mathrm {P_{2}} \ \)で反比例に近い分布になる。また,\( \ \mathrm {P_{1}} \ \)と\( \ \mathrm {P_{2}} \ \)に電位差がある図が正しい。よって,(ハ)の波形が正しい。
(2)解答:ホ
スイッチ\( \ \mathrm {S} \ \)を\( \ 1 \ \)側に閉じ,回路が平衡したとき,回路は図2-1のように書き換えることができる。
図2-1より,回路の平衡条件は,
\[
\begin{eqnarray}
R_{K}\left( R_{1}+R_{2}\right) &=&R_{Q}R_{W} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
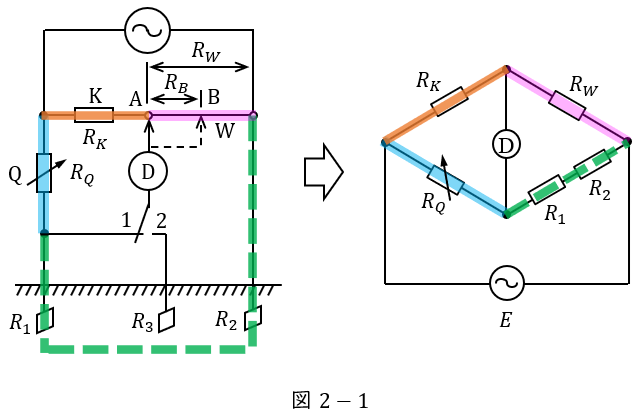
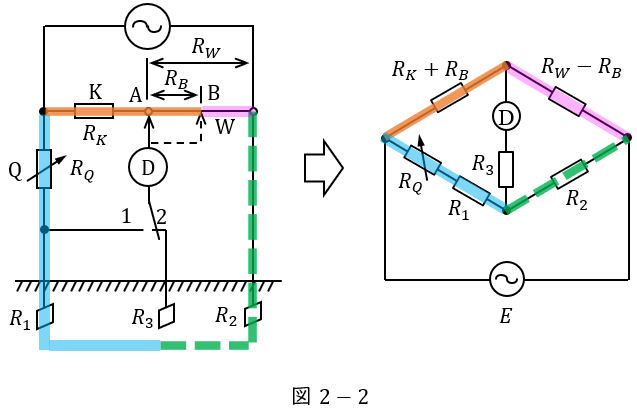
(3)解答:ヌ
スイッチ\( \ \mathrm {S} \ \)を\( \ 2 \ \)側に閉じ,回路が平衡したとき,回路は図2-2のように書き換えることができる。
図2-2より,回路の平衡条件は,
\[
\begin{eqnarray}
\left( R_{Q}+R_{1}\right) \left( R_{W}-R_{B}\right) &=&R_{2} \left( R_{K}+R_{B}\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ヨ
②式((3)解答式)を変形すると,
\[
\begin{eqnarray}
R_{2} &=&\frac {\left( R_{Q}+R_{1}\right) \left( R_{W}-R_{B}\right) }{R_{K}+R_{B}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,これを①式((2)解答式)に代入して整理すると,
\[
\begin{eqnarray}
R_{K}\left\{ R_{1}+\frac {\left( R_{Q}+R_{1}\right) \left( R_{W}-R_{B}\right) }{R_{K}+R_{B}}\right\} &=&R_{Q}R_{W} \\[ 5pt ]
R_{1}+\frac {\left( R_{Q}+R_{1}\right) \left( R_{W}-R_{B}\right) }{R_{K}+R_{B}} &=&\frac {R_{Q}R_{W}}{R_{K}} \\[ 5pt ]
R_{1}\left( R_{K}+R_{B}\right) +\left( R_{Q}+R_{1}\right) \left( R_{W}-R_{B}\right) &=&\frac {R_{Q}R_{W}\left( R_{K}+R_{B}\right) }{R_{K}} \\[ 5pt ]
R_{1}R_{K}+R_{1}R_{B}+R_{Q}R_{W}-R_{B}R_{Q}+R_{1}R_{W}-R_{1}R_{B} &=&\frac { R_{Q}R_{W}R_{K}+R_{B}R_{Q}R_{W} }{R_{K}} \\[ 5pt ]
R_{1}R_{K}+R_{Q}R_{W}-R_{B}R_{Q}+R_{1}R_{W} &=&R_{Q}R_{W}+\frac { R_{B}R_{Q}R_{W} }{R_{K}} \\[ 5pt ]
R_{1}R_{K}-R_{B}R_{Q}+R_{1}R_{W} &=&\frac { R_{B}R_{Q}R_{W} }{R_{K}} \\[ 5pt ]
R_{1}R_{K}+R_{1}R_{W} &=&R_{B}R_{Q}+\frac { R_{B}R_{Q}R_{W} }{R_{K}} \\[ 5pt ]
R_{1}\left( R_{K}+R_{W}\right) &=&\frac { R_{B}R_{Q}R_{K}+R_{B}R_{Q}R_{W} }{R_{K}} \\[ 5pt ]
&=&\frac { R_{B}R_{Q}\left( R_{K}+R_{W}\right) }{R_{K}} \\[ 5pt ]
R_{1}&=&\frac { R_{B}R_{Q}}{R_{K}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ト
(4)解答式より,滑り線抵抗器\( \ \mathrm {W} \ \)を予め細かく目盛っておく,すなわち\( \ R_{B} \ \)を正確に求めることができれば,\( \ \displaystyle \frac { R_{Q}}{R_{K}} \ \)から\( \ R_{1} \ \)を求めることができる。












 【令和8年度版2種一次試験】
【令和8年度版2種一次試験】








 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは