《理論》〈電磁気〉[H22:問5]円筒導体及び円柱導体の磁界分布及び電界分布に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，円筒導体及び円柱導体の磁界分布及び電界分布に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる式又は数値を解答群の中から選びなさい。ただし，真空の透磁率を$ \ \mu _{0} \ $，真空の誘電率を$ \ \varepsilon _{0} \ $とする。

a.図1に示すように，無限長で半径$ \ a \ $の，厚さが無視できる円筒導体に一様に直流電流$ \ I \ $が流れている。このとき，中心軸から$ \ r \ $離れた点$ \ \mathrm {P} \ $における磁束密度の大きさは，円筒内部$ \ \left( r＜a\right) \ $では$ \ \fbox {　（１）　} \ $であり，円筒外部$ \ \left( a＜r\right) \ $では$ \ \fbox {　（２）　} \ $である。

b.図2に示すように，無限長で半径$ \ a \ $の円柱導体（透磁率$ \ \mu _{0} \ $）の内部に一様に直流電流$ \ I \ $が流れている。このとき，中心軸から$ \ r \ $離れた点$ \ \mathrm {P} \ $における磁束密度の大きさは，円柱内部$ \ \left( r＜a\right) \ $では$ \ \fbox {　（３）　} \ $であり，円柱外部$ \ \left( a＜r\right) \ $では上記a.の円筒導体の場合と同じ$ \ \fbox {　（２）　} \ $である。

c.図3に示すように，半径が異なり厚さが無視できる十分長い円筒導体が二つあり，同心に配置されている。その一端に電圧$ \ V \ $の直流電源，他端に抵抗$ \ R \ $の負荷が接続されている。内側円筒導体の半径を$ \ a \ $，外側円筒導体の半径を$ \ b \ $とするとき，中心軸から$ \ r \ $離れた点$ \ \mathrm {P} \ $における周方向の磁界の強さは導体間$ \ \left( a＜r＜b\right) \ $において，$ \ \fbox {　（２）　} \ $を$ \ \mu _{0} \ $で除し，$ \ \displaystyle I=\frac {V}{R} \ $の関係を用いて$ \ I \ $を消去することにより$ \ \fbox {　（４）　} \ $である。ただし，電流は円筒導体中を軸方向に一様に流れるものとする。

d.図3の場合，内側導体と外側導体には電位差$ \ V \ $が存在するため，向かい合う両導体には誘導電荷が生じ，導体間には電界が生じる。ここで，単位長さ当たり$ \ \lambda \ $の電荷密度を仮定すると，中心軸から$ \ r \ $離れた点$ \ \mathrm {P} \ $における径方向の電界の大きさ$ \ E_{\mathrm {r}} \ $は，導体間$ \ \left( a＜r＜b\right) \ $で$ \ \displaystyle E_{\mathrm {r}}=\frac {\lambda}{2\pi \varepsilon _{0}r} \ $となる。

$ \ \displaystyle V=-\int _{b}^{a}E_{\mathrm {r}}\mathrm {d}r=\frac {\lambda }{2\pi \varepsilon _{0}}\ln \frac {b}{a} \ $の関係を用いて$ \ \lambda \ $を消去すると，$ \ E_{\mathrm {r}} \ $は$ \ \fbox {　（５）　} \ $である。

〔問5の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {I}{2\pi r}　　　　　&（ロ）&　\frac {V}{4\pi r^{2}R}　　　　　&（ハ）&　\frac {\mu _{0}I}{4\pi r^{2}} \\[ 5pt ] &（ニ）&　\frac {V}{\displaystyle r\ln \frac {b}{a}}　　　　　&（ホ）&　\frac {3\mu _{0}Ir^{2}}{4\pi a^{3}}　　　　　&（ヘ）&　\frac {\displaystyle r\ln \frac {b}{a}}{4\pi \varepsilon _{0}V} \\[ 5pt ] &（ト）&　\mu _{0}I　　　　　&（チ）&　\frac {V}{2\pi rR}　　　　　&（リ）&　0 \\[ 5pt ] &（ヌ）&　\frac {\mu _{0}Ir}{2\pi a^{2}}　　　　　&（ル）&　\frac {V}{\pi r^{2}R}　　　　&（ヲ）&　\frac {\mu _{0}I}{2\pi r} \\[ 5pt ] &（ワ）&　\frac {Vr}{\displaystyle 4\pi ^{2}{\varepsilon _{0}}^{2}\ln \frac {b}{a}}　　　　　&（カ）&　\frac {\mu _{0}I}{\pi r^{2}}　　　　&（ヨ）&　\frac {\mu _{0}I}{2\pi r^{2}} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

円筒導体もしくは円柱導体の周りの磁界分布及び電界分布に関する問題です。
特に図1と図2の違いは電験$ \ 2 \ $種では非常に重要な内容となりますので，しっかりと理解する必要があります。
余裕があれば，問題文dの文章中の$ \ \displaystyle E_{\mathrm {r}}=\frac {\lambda}{2\pi \varepsilon _{0}r} \ $や$ \ \displaystyle V=-\int _{b}^{a}E_{\mathrm {r}}\mathrm {d}r=\frac {\lambda }{2\pi \varepsilon _{0}}\ln \frac {b}{a} \ $も自力で導き出せるように練習しておきましょう。

1.ガウスの法則
$ \ Q \ \mathrm {[C]} \ $から出る電気力線は$ \ \displaystyle \frac {Q}{\varepsilon } \ $本であり，電界$ \ E \ \mathrm {[V / m]} \ $との関係は，任意の閉曲面において，
\[
\begin{eqnarray}
\int _{S} \boldsymbol E \cdot \mathrm {d}\boldsymbol S &=& \frac {Q}{\varepsilon } \\[ 5pt ] \end{eqnarray}
\] となり，これをガウスの法則といいます。

2.アンペールの周回積分の法則
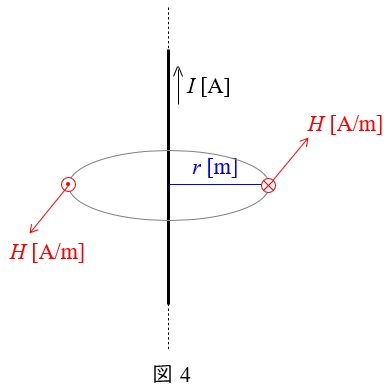
図4のように無限長直線電流$ \ I \ \mathrm {[A]} \ $が流れているとき，電線から距離$ \ r \ \mathrm {[m]} \ $の位置での磁界の強さ$ \ H \ \mathrm {[A / m]} \ $は，
\[
\begin{eqnarray}
H&=&\frac {I}{2\pi r} \\[ 5pt ] \end{eqnarray}
\] となります。

3.磁束密度$ \ B \ $と磁界の大きさ$ \ H \ $の関係
透磁率が$ \ \mu \ \mathrm {[H / m]} \ $の時，磁束密度$ \ B \ \mathrm {[T]} \ $と磁界の大きさ$ \ H \ \mathrm {[A / m]} \ $の関係は，
\[
\begin{eqnarray}
B&=&\mu H \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：リ
円筒内部$ \ \left( r＜a\right) \ $においては点$ \ \mathrm {P} \ $の内側に流れる電流は$ \ 0 \ $なので，磁界の大きさは$ \ 0 \ $であり磁束密度の大きさも$ \ 0 \ $となる。

(2)解答：ヲ
円筒外部$ \ \left( a＜r\right) \ $においては点$ \ \mathrm {P} \ $の内側に流れる電流は$ \ I \ $なので，磁界の大きさ$ \ H_{1} \ $は，ワンポイント解説「2.アンペールの周回積分の法則」の通り，
\[
\begin{eqnarray}
H_{1}&=&\frac {I}{2\pi r} \\[ 5pt ] \end{eqnarray}
\] となり，磁束密度の大きさ$ \ B_{1} \ $は，ワンポイント解説「3.磁束密度$ \ B \ $と磁界の大きさ$ \ H \ $の関係」の通り，
\[
\begin{eqnarray}
B_{1}&=&\mu _{0} H_{1} \\[ 5pt ] &=&\frac {\mu _{0}I}{2\pi r} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ヌ
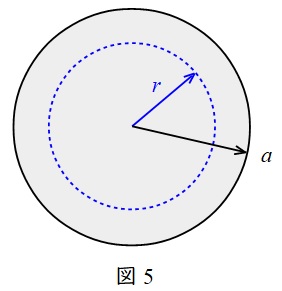
図5の断面図に示すように，円柱内部$ \ \left( r＜a\right) \ $において，点$ \ \mathrm {P} \ $の内側に流れる電流の大きさ$ \ I^{\prime } \ $は，
\[
\begin{eqnarray}
I^{\prime }&=&\frac {\pi r^{2}}{\pi a^{2}}I \\[ 5pt ] &=&\frac {r^{2}}{a^{2}}I \\[ 5pt ] \end{eqnarray}
\] となるので，磁界の大きさ$ \ H_{2} \ $は，ワンポイント解説「2.アンペールの周回積分の法則」の通り，
\[
\begin{eqnarray}
H_{2}&=&\frac {I^{\prime }}{2\pi r} \\[ 5pt ] &=&\frac {\displaystyle \frac {r^{2}}{a^{2}}I}{2\pi r} \\[ 5pt ] &=&\frac {Ir}{2\pi a^{2}} \\[ 5pt ] \end{eqnarray}
\] となり，磁束密度の大きさ$ \ B_{2} \ $は，ワンポイント解説「3.磁束密度$ \ B \ $と磁界の大きさ$ \ H \ $の関係」の通り，
\[
\begin{eqnarray}
B_{2}&=&\mu _{0} H_{2} \\[ 5pt ] &=&\frac {\mu _{0}Ir}{2\pi a^{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：チ
問題文に沿って(2)解答式を$ \ \mu _{0} \ $で割ると，$ \ \displaystyle H_{1}=\frac {I}{2\pi r} \ $であるので，これに$ \ \displaystyle I=\frac {V}{R} \ $を代入すれば，
\[
\begin{eqnarray}
H_{1}&=&\frac {I}{2\pi r} \\[ 5pt ] &=&\frac {\displaystyle \frac {V}{R}}{2\pi r} \\[ 5pt ] &=&\frac {V}{2\pi rR} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ニ
$ \ \displaystyle E_{\mathrm {r}}=\frac {\lambda}{2\pi \varepsilon _{0}r} \ $すなわち$ \ \lambda =2\pi \varepsilon _{0}rE_{\mathrm {r}} \ $及び$ \ \displaystyle V=\frac {\lambda }{2\pi \varepsilon _{0}}\ln \frac {b}{a} \ $すなわち$ \ \displaystyle \lambda =\frac {2\pi \varepsilon _{0}V}{\displaystyle \ln \frac {b}{a}} \ $より，$ \ \lambda \ $を消去すれば，
\[
\begin{eqnarray}
2\pi \varepsilon _{0}rE_{\mathrm {r}}&=&\frac {2\pi \varepsilon _{0}V}{\displaystyle \ln \frac {b}{a}} \\[ 5pt ] rE_{\mathrm {r}}&=&\frac {V}{\displaystyle \ln \frac {b}{a}} \\[ 5pt ] E_{\mathrm {r}}&=&\frac {V}{\displaystyle r\ln \frac {b}{a}} \\[ 5pt ] \end{eqnarray}
\]