《理論》〈電子理論〉[H24:問4]pn接合ダイオードに関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，$ \ \mathrm {pn} \ $接合ダイオードの降伏に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまるものを解答群の中から選びなさい。

$ \ \mathrm {pn} \ $接合ダイオードにおいて，空乏層内での電界の最大値が$ \ 10^{5} \ \mathrm {[V／cm]} \ $程度の電界$ \ E_{\mathrm {crit}} \ $を超えると降伏が起こる。いま$ \ E_{\mathrm {crit}} \ $は不純物濃度によらず一定とし，$ \ \mathrm {p} \ $形半導体は一様な不純物濃度$ \ N_{\mathrm {A}} \ $でドーピングされ，$ \ \mathrm {n} \ $形半導体は一様な不純物濃度$ \ N_{\mathrm {D}} \ $でドーピングされているとする。単位電荷の絶対値を$ \ q \ $とする。

$ \ \mathrm {p} \ $形半導体の空乏層厚を$ \ l_{\mathrm {p}} \ $，$ \ \mathrm {n} \ $形半導体の空乏層厚を$ \ l_{\mathrm {n}} \ $とすると，$ \ \mathrm {p} \ $層の空乏層内の単位面積当たりの全電荷量は$ \ \fbox {　（１）　} \ $であり，$ \ \mathrm {n} \ $層の空乏層内の単位面積当たりの全電荷量は$ \ \fbox {　（２）　} \ $である。$ \ \mathrm {p} \ $層の空乏層と$ \ \mathrm {n} \ $層の空乏層では，お互いに空乏化した不純物を作り出す電荷は打ち消しあっているので，これらの絶対値は等しい。したがって，$ \ l_{\mathrm {p}} \ $と$ \ l_{\mathrm {n}} \ $の比は$ \ \displaystyle \frac {N_{\mathrm {A}}}{N_{\mathrm {D}}} \ $から計算できる。

空乏層内での電界は空乏層内の電荷により作られ，電界が最も強いところでは$ \ \mathrm {p} \ $側の空乏層での電荷すべてが寄与することから，$ \ \fbox {　（１）　} \ $を半導体の誘電率$ \ \varepsilon \ $で割れば最も強い電界が求まる。電界が最も強いところの大きさが$ \ E_{\mathrm {crit}} \ $になると降伏が起こるので，降伏時の空乏層厚$ \ l_{\mathrm {p}} \ $は$ \ E_{\mathrm {crit}} \ $を用いて$ \ \fbox {　（３）　} \ $と表される。

電界は空乏層が始まるところでは零であり，そこから線形的に増えていくことから，電界は空乏層が始まった場所から距離に比例した関数となり，$ \ \mathrm {p} \ $側の空乏層での電圧降下の大きさはその積分から$ \ l_{\mathrm {p}} \ $を用いて表すと$ \ \fbox {　（４）　} \ $となる。ここで，$ \ \displaystyle \frac {N_{\mathrm {A}}}{N_{\mathrm {D}}} \ $は，$ \ 1 \ $より十分小さいとすると$ \ \fbox {　（４）　} \ $のみで$ \ \mathrm {pn} \ $接合ダイオードの電圧降下をほぼ説明できる。

以上のことから，$ \ E_{\mathrm {crit}} \ $を用いて電圧降下を表すと$ \ \fbox {　（５）　} \ $となる。通常この電圧が降伏電圧となることから，不純物濃度が低いほうが降伏電圧を高くできることがわかる。

〔問4の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {ql_{\mathrm {p}}N_{\mathrm {A}}^{2}}{2\varepsilon }　　　&（ロ）&　q\varepsilon N_{\mathrm {A}}E_{\mathrm {crit}}　　　&（ハ）&　-ql_{\mathrm {p}}N_{\mathrm {A}} \\[ 5pt ] &（ニ）&　q\varepsilon N_{\mathrm {A}}{E_{\mathrm {crit}}}^{2} 　　　&（ホ）&　ql_{\mathrm {n}}N_{\mathrm {D}}　　　&（ヘ）&　\frac {ql_{\mathrm {p}}^{2}N_{\mathrm {A}}}{2\varepsilon } \\[ 5pt ] &（ト）&　\frac {\varepsilon {E_{\mathrm {crit}}}^{2}}{2qN_{\mathrm {A}}}　　　&（チ）&　ql_{\mathrm {n}}N_{\mathrm {A}}　　　　&（リ）&　\frac {ql_{\mathrm {p}}^{2}N_{\mathrm {A}}}{\varepsilon } \\[ 5pt ] &（ヌ）&　ql_{\mathrm {p}}N_{\mathrm {A}}　　　&（ル）&　-ql_{\mathrm {n}}N_{\mathrm {D}}　　　&（ヲ）&　\frac {\varepsilon E_{\mathrm {crit}}}{qN_{\mathrm {A}}} \\[ 5pt ] &（ワ）&　\frac {2\varepsilon {E_{\mathrm {crit}}}^{2}}{qN_{\mathrm {A}}}　　　&（カ）&　\frac {q{E_{\mathrm {crit}}}}{\varepsilon N_{\mathrm {A}}} 　　　&（ヨ）&　ql_{\mathrm {p}}N_{\mathrm {D}} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

かなり難易度が高い問題と言えると思います。私も１種の勉強をしたときに専門書で見たことがあるような内容です。かなりの受験生が苦労した問題であると思いますが，選択肢毎の関連性や文章を読み解くことで正答が導き出せるようになると良いと思います。

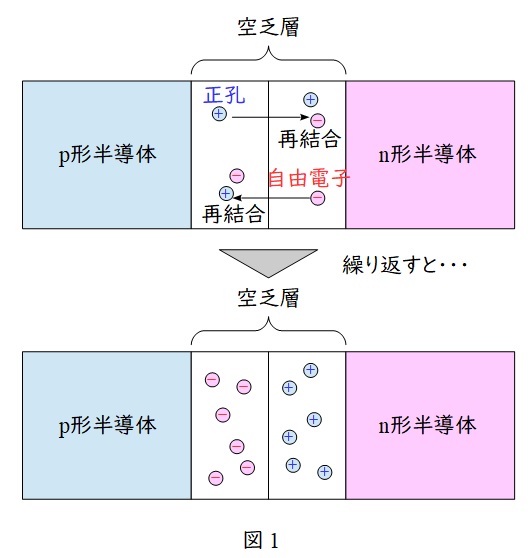
1.$ \ \mathrm {pn} \ $接合ダイオードにおける電荷の分布
図1のように$ \ \mathrm {p} \ $形半導体と$ \ \mathrm {n} \ $形半導体で$ \ \mathrm {pn} \ $接合すると，$ \ \mathrm {p} \ $形半導体の正孔が$ \ \mathrm {n} \ $形半導体に移動し，$ \ \mathrm {n} \ $形半導体中の電子と再結合し消滅します。すると，$ \ \mathrm {n} \ $形半導体中に正の電荷を持つ不純物がドーピングされることになります。
同様に$ \ \mathrm {n} \ $形半導体の自由電子が$ \ \mathrm {p} \ $形半導体に移動し，$ \ \mathrm {p} \ $形半導体中の正孔と再結合し消滅します。すると，$ \ \mathrm {p} \ $形半導体中に負の電荷を持つ不純物がドーピングされることになります。
したがって，これを繰り返すと図１の下のように$ \ \mathrm {n} \ $形半導体が＋で$ \ \mathrm {p} \ $形半導体が−となる空乏層ができ，その間には電界が発生することになります。

【解答】

(1)解答：ハ
題意より，$ \ \mathrm {p} \ $形半導体は一様な不純物濃度$ \ N_{\mathrm {A}} \ $でドーピングされており，ワンポイント解説「1.$ \ \mathrm {pn} \ $接合ダイオードにおける電荷の分布」の通り，$ \ \mathrm {p} \ $形半導体での電荷はマイナスであるから，単位面積当たりの全電荷量$ \ Q_{\mathrm {p}} \ $は，
\[
\begin{eqnarray}
Q_{\mathrm {p}} &=&-ql_{\mathrm {p}}N_{\mathrm {A}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ホ
(1)と同様に，$ \ \mathrm {n} \ $形半導体は一様な不純物濃度$ \ N_{\mathrm {D}} \ $でドーピングされており，ワンポイント解説「1.$ \ \mathrm {pn} \ $接合ダイオードにおける電荷の分布」の通り，$ \ \mathrm {n} \ $形半導体での電荷はプラスであるから，単位面積当たりの全電荷量$ \ Q_{\mathrm {n}} \ $は，
\[
\begin{eqnarray}
Q_{\mathrm {n}} &=&ql_{\mathrm {n}}N_{\mathrm {D}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ヲ
題意より，$ \ Q_{\mathrm {p}} \ $を半導体の誘電率$ \ \varepsilon \ $で割れば最も強い電界が求まり，電界が最も強いところの大きさが$ \ E_{\mathrm {crit}} \ $になると降伏が起こるので，
\[
\begin{eqnarray}
E_{\mathrm {crit}} &=&\frac {Q_{\mathrm {p}}}{\varepsilon } \\[ 5pt ] &=&-\frac {ql_{\mathrm {p}}N_{\mathrm {A}}}{\varepsilon } \\[ 5pt ] \end{eqnarray}
\] となるので，その大きさは，
\[
\begin{eqnarray}
E_{\mathrm {crit}}&=&\frac {ql_{\mathrm {p}}N_{\mathrm {A}}}{\varepsilon } \\[ 5pt ] \end{eqnarray}
\] となる。したがって，空乏層厚$ \ l_{\mathrm {p}} \ $は，
\[
\begin{eqnarray}
l_{\mathrm {p}}&=&\frac {\varepsilon E_{\mathrm {crit}}}{qN_{\mathrm {A}}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ヘ
題意より，電界は$ \ \mathrm {pn} \ $接合の界面が最も大きく，空乏層がはじまるところが零であるため，空乏層のはじまる場所から距離$ \ l \ $における電界の大きさは，
\[
\begin{eqnarray}
E&=&\frac {qN_{\mathrm {A}}}{\varepsilon }l \\[ 5pt ] \end{eqnarray}
\] となる。よって，$ \ \mathrm {p} \ $形半導体の空乏層全体での電圧降下$ \ V_{\mathrm {p}} \ $は，
\[
\begin{eqnarray}
V_{\mathrm {p}}&=&\int _{0}^{l_{\mathrm {p}}}\frac {qN_{\mathrm {A}}}{\varepsilon }l \mathrm {d}l \\[ 5pt ] &=&\frac {qN_{\mathrm {A}}}{\varepsilon }\left[ \frac {l^{2}}{2}\right] _{0}^{l_{\mathrm {p}}} \\[ 5pt ] &=&\frac {ql_{\mathrm {p}}^{2}N_{\mathrm {A}}}{2\varepsilon } \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ト
(4)の解答式に(3)の解答式を代入すると，
\[
\begin{eqnarray}
V_{\mathrm {p}}&=&\frac {ql_{\mathrm {p}}^{2}N_{\mathrm {A}}}{2\varepsilon } \\[ 5pt ] &=&\frac {qN_{\mathrm {A}}}{2\varepsilon }\left( \frac {\varepsilon E_{\mathrm {crit}}}{qN_{\mathrm {A}}}\right) ^{2} \\[ 5pt ] &=&\frac {\varepsilon {E_{\mathrm {crit}}}^{2}}{2qN_{\mathrm {A}}} \\[ 5pt ] \end{eqnarray}
\] と求められる。