《理論》〈電磁気〉[H27:問1]誘電体又は導電体に満たされた同軸円筒導体に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
- 2.1 【関連する「電気の神髄」記事】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，誘電体又は導電体に満たされた同軸円筒導体に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選びなさい。

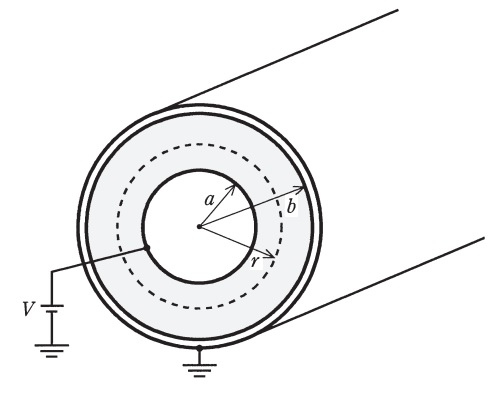
無限に長い同軸円筒導体を想定し，図に示した断面のように，内部導体の外半径を$ \ a \ $，外部導体の内半径を$ \ b \ $とする。この同軸円筒導体の外部導体を接地し，内部導体に電圧$ \ V \ $を印加したときの半径$ \ r \ $の位置における電界の強さ$ \ E(r) \ $とする。

まず，内外導体間($ \ a < r < b \ $)を誘電率$ \ \varepsilon \ $で導電率零の誘電体で満たす。このとき，単位長さ当たりの内部導体に蓄えられている電荷を$ \ Q \ $とし，半径$ \ r \ $の位置における電束密度の大きさ$ \ D(r) \ $と$ \ Q \ $との関係を求めると，$①$式のようになる。 \[ D(r)=\fbox {　（１）　}　・・・・・・・・・・　① \] また，$ \ E(r) \ $と$ \ D(r) \ $との間には②式の関係がある。 \[ D(r)=\varepsilon E(r) \ 　・・・・・・・・・・・　② \] $ \ E(r) \ $を$ \ r \ $について$ \ a \ $から$ \ b \ $まで積分した値が円筒間の電位差$ \ V \ $に等しいことから，$ \ V \ $と$ \ Q \ $の関係が得られる。よって，この同軸円筒導体の単位長さ当たりの静電容量$ \ C \ $は$③$式のようになる。 \[ C=\fbox {　（２）　} \ 　・・・・・・・・・・・　③ \] 次に，誘電体を除去したのち，内外導体間を誘電率$ \ \varepsilon _{0} \ $(真空と同じ)で導電率$ \ \sigma \ $の導電体で満たす。内外導体間に流れる単位長さ当たりの定常電流を$ \ I \ $とすると，半径$ \ r \ $の位置において電流密度の大きさ$ \ J(r) \ $は一様であり，④式で表される。 \[ J(r)=\fbox {　（３）　}　・・・・・・・・・・　④ \] $ \ J(r) \ $と$ \ E(r) \ $との間に成り立つオームの法則は，$⑤$式で表される。 \[ J(r)=\fbox {　（４）　}　・・・・・・・・・・　⑤ \] $①$式と$④$式，$②$式と$⑤$式とを比べると，導電体における$ \ I \ $，$ \ J(r) \ $，$ \ \sigma \ $は，誘電体における，$ \ Q \ $，$ \ D(r) \ $，$ \ \varepsilon \ $と対応させられる。このようなアナロジーを利用して，$③$式から導電体で満たされた同軸円筒導体の単位長さ当たりのコンダクタンス$G$は$⑥$式のように求められる。 \[ G=\fbox {　（５）　} \ 　・・・・・・・・・・・　⑥ \]

〔問1の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {Q}{4\pi r^{2}}　　　&（ロ）&　\frac {2\pi \varepsilon a^{2}b^{2}}{3(b^{2}-a^{2})}　　　&（ハ）&　\varepsilon _{0} \sigma E(r) \\[ 5pt ] &（ニ）&　\frac {2\pi \sigma a^{2}b^{2}}{3(b^{2}-a^{2})}　　　&（ホ）&　\frac {I}{2\pi r}　　　&（ヘ）&　\sigma E(r) \\[ 5pt ] &（ト）&　\frac {E(r)}{\sigma}　　　&（チ）&　\frac {3I}{4\pi r^{3}}　　　　&（リ）&　\frac {Q}{2\pi r} \\[ 5pt ] &（ヌ）&　\frac {2\pi \varepsilon }{\displaystyle \ln \frac {b}{a}}　　　&（ル）&　\frac {2\pi \sigma }{\displaystyle \ln \frac {b}{a}}　　　&（ヲ）&　\frac {4\pi \sigma ab}{b-a} \\[ 5pt ] &（ワ）&　\frac {I}{4\pi r^{2}}　　　&（カ）&　\frac {4\pi \varepsilon ab}{b-a}　　　&（ヨ）&　\frac {3Q}{4\pi r^{3}}
\end{eqnarray}
\]

【ワンポイント解説】

本問は典型的なガウスの定理を利用した問題ですが，同心球と勘違いするとすべて誤答となってしまう可能性があります。図と問題文をよく読んで間違えないように注意して下さい。

1.ガウスの定理
$ \ Q [ \mathrm {C} ] \ $から出る電気力線は$ \ \displaystyle \frac {Q}{\varepsilon } \ $本であり，電界$ \ E \ $との関係は，任意の閉曲面において，
\[
\int _{S} \boldsymbol E \mathrm {d}\boldsymbol S = \frac {Q}{\varepsilon }
\] となります。閉局面が同軸円筒導体であれば，単位長さ当たりの電界$ \ E \ $は，
\[
\begin{eqnarray}
2\pi r E &=& \frac {Q}{\varepsilon } \\[ 5pt ] E &=& \frac {Q}{2\pi \varepsilon r}
\end{eqnarray}
\] となります。

2.空間上の電位$ \ V \ $
中心からの距離$ \ r \ $に関する電界$ \ E_{\mathrm {r}} \ $が与えられている時，その場所の電位$ \ V \ $は，
\[
V=-\int _{\infty }^{r}E_{\mathrm {r}}\mathrm {d}r
\] で求められます。

【関連する「電気の神髄」記事】

　　円筒導体の静電容量
　　同軸円筒導体の静電容量まとめ

【解答】

(1)解答：リ
ガウスの定理より，
\[
\begin{eqnarray}
2\pi r D(r) &=& Q \\[ 5pt ] D(r) &=& \frac {Q}{2\pi r}
\end{eqnarray}
\] と求められる。

(2)解答：ヌ
②より，$ \ D(r)=\varepsilon E(r) \ $であるから，
\[
\begin{eqnarray}
E(r) &=& \frac {D(r)}{\varepsilon } \\[ 5pt ] &=& \frac {Q}{2\pi \varepsilon r}
\end{eqnarray}
\] となり，ワンポイント解説「2.空間上の電位$ \ V \ $」より，
\[
\begin{eqnarray}
V &=& \int _{a }^{b}E(r)\mathrm {d}r \\[ 5pt ] &=& \int _{a }^{b}\frac {Q}{2\pi \varepsilon r}\mathrm {d}r \\[ 5pt ] &=& \frac {Q}{2\pi \varepsilon }\left[ \ln r\right] _{a }^{b} \\[ 5pt ] &=& \frac {Q}{2\pi \varepsilon }\left[ \ln b-\ln a \right] \\[ 5pt ] &=& \frac {Q}{2\pi \varepsilon }\ln \frac {b}{a} \\[ 5pt ] \end{eqnarray}
\] となる。よって静電容量$ \ \displaystyle C=\frac {Q}{V} \ $より，
\[
\begin{eqnarray}
C &=& \frac {Q}{V} \\[ 5pt ] &=& \frac {Q}{\displaystyle \frac {Q}{2\pi \varepsilon }\ln \frac {b}{a}} \\[ 5pt ] &=& \frac {2\pi \varepsilon }{\displaystyle \ln \frac {b}{a}}
\end{eqnarray}
\] と求められる。

(3)解答：ホ
単位長さ当たりの電流$ \ I \ $と電流密度$ \ J(r) \ $との関係は，
\[
\begin{eqnarray}
I &=& 2\pi r \times J(r) \\[ 5pt ] J(r)&=& \frac {I}{2\pi r} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ヘ
$ \ J(r) \ $と$ \ E(r) \ $との間に成り立つオームの法則は，
\[
J(r)=\sigma E(r)
\] となる。

(5)解答：ル
$ \ \displaystyle G=\frac {I}{V} \ $は誘電体においては$ \ \frac {Q}{V}=C \ $に対応するから，
\[
\begin{eqnarray}
&&\frac {Q}{V}=\frac {2\pi \varepsilon }{\displaystyle \ln \frac {b}{a}} \\[ 5pt ] &&　→　\frac {I}{V}=\frac {2\pi \sigma }{\displaystyle \ln \frac {b}{a}}
\end{eqnarray}
\] と求められる。