《理論》〈電気回路〉[H28:問2] 直流回路における諸計算に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★☆☆☆☆（易しい）

次の文章は，直流回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

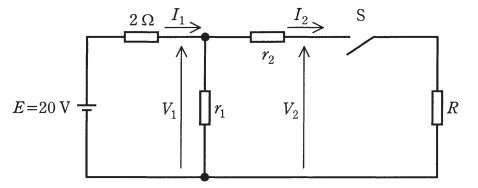
図のように，直流電圧源$ \ E=20 \ \mathrm {V} \ $に，$ \ 2 \ \mathrm {\Omega } \ $の抵抗，抵抗$ \ r_{1} \ $，$ \ r_{2} \ $，スイッチ$ \ \mathrm {S} \ $及び負荷抵抗$ \ R \ $を接続した。

(a)　スイッチ$ \ \mathrm {S} \ $が開いているとき，$ \ V_{2}=15 \ \mathrm {V} \ $かつ回路全体の消費電力は$ \ 50 \ \mathrm {W} \ $であった。

(b)　スイッチ$ \ \mathrm {S} \ $が閉じているとき，$ \ \displaystyle \frac {V_{1}}{I_{1}}=\frac {V_{2}}{I_{2}} \ $かつ回路全体の消費電力は$ \ 100 \ \mathrm {W} \ $であった。

回路全体の消費電力あるいは分圧比を考慮すると，(a)の結果から，$ \ r_{1}= \ \fbox {　（１）　} \ \Omega \ $となる。
次に(b)の状態における電圧，電流を考える。回路全体の消費電力から，$ \ I_{1}= \ \fbox {　（２）　} \ \mathrm {A} \ $となる。$ \ \displaystyle \frac {V_{1}}{I_{1}}=\frac {V_{2}}{I_{2}}=R \ $と$ \ V_{1}=E-2I_{1} \ $に注意すると，$ \ \displaystyle \frac {V_{1}}{I_{1}}=\frac {V_{2}}{I_{2}}=R= \ \fbox {　（３）　} \ \Omega \ $となる。(b)のとき，$ \ r_{1} \ $と$ \ r_{2}+R \ $の合成抵抗は$ \ R \ $と等しいので$ \ r_{2}= \ \fbox {　（４）　} \ \Omega \ $であり，分流比を使うと$ \ I_{2}= \ \fbox {　（５）　} \ \mathrm {A} \ $となる。

〔問2の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {1}{5}　　　&（ロ）&　\frac {2}{5}　　　&（ハ）&　1 \\[ 5pt ] &（ニ）&　2　　　&（ホ）&　\frac {7}{3}　　　&（ヘ）&　\frac {8}{3} \\[ 5pt ] &（ト）&　3　　　&（チ）&　\frac {10}{3} 　　　&（リ）&　4 \\[ 5pt ] &（ヌ）&　5 　　　&（ル）&　6　　　&（ヲ）&　7　 \\[ 5pt ] &（ワ）&　8　　　&（カ）&　9　　　&（ヨ）&　10
\end{eqnarray}
\]

【ワンポイント解説】

電気回路の基本的な内容を問う問題です。理論科目を合格するためには本問レベルの問題は確実に完答できるようにしておきたいところです。

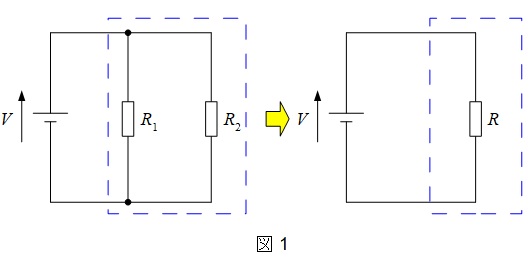
1.並列回路の合成抵抗
図1の回路において，合成抵抗$ \ R \ $は，
\[
\begin{eqnarray}
\frac {1}{R} &=& \frac {1}{R_{1}}+\frac {1}{R_{2}} \\[ 5pt ] R &=& \frac {R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

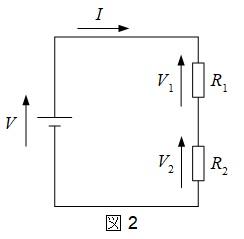
2.分圧比
図2の回路において，$ \ R_{1} \ $にかかる電圧$ \ V_{1} \ $と$ \ R_{2} \ $にかかる電圧$ \ V_{2} \ $は，
\[
\begin{eqnarray}
V_{1}&=&\frac {R_{1}}{R_{1}+R_{2}}V \\[ 5pt ] V_{2}&=&\frac {R_{2}}{R_{1}+R_{2}}V \\[ 5pt ] \end{eqnarray}
\] となります。

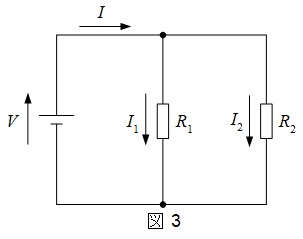
3.分流比
図3の回路において，$ \ R_{1} \ $に流れる電流$ \ I_{1} \ $と$ \ R_{2} \ $に流れる電流$ \ I_{2} \ $は，
\[
\begin{eqnarray}
I_{1}&=&\frac {R_{2}}{R_{1}+R_{2}}I \\[ 5pt ] I_{2}&=&\frac {R_{1}}{R_{1}+R_{2}}I \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：ル
スイッチ$ \ \mathrm {S} \ $が開いているとき，$ \ I_{2}=0 \ $であるから，$ \ V_{1}=V_{2}=15 \ \mathrm {V} \ $である。
分圧比の関係から，
\[
\begin{eqnarray}
V_{1}&=&\frac {r_{1}}{2+r_{1}}E \\[ 5pt ] \end{eqnarray}
\] であるから，各値を代入し，$ \ r_{1} \ $を求めると，
\[
\begin{eqnarray}
&&15 &=& \frac {r_{1}}{2+r_{1}}\times 20 \\[ 5pt ] &⇔& r_{1} &=& 6 \ \mathrm { [ \Omega ] } \\[ 5pt ] \end{eqnarray}
\] となる。

(2)解答：ヌ
回路全体の消費電力$ \ W \ $は，電源から送られる電力$ \ P \ $と等しいので，
\[
\begin{eqnarray}
W &=& P = EI_{1} \\[ 5pt ] 100&=& 20\times I_{1} \\[ 5pt ] I_{1} &=& 5 \ \mathrm { [ A ] } \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ニ
$ \ E=20 \ \mathrm {V} \ $，$ \ I_{1} = 5 \ \mathrm { A } \ $であるから，
\[
\begin{eqnarray}
V_{1} &=& E-2I_{1} \\[ 5pt ] &=& 20-2\times 5 \\[ 5pt ] &=& 10 \ \mathrm { [ V ] } \\[ 5pt ] \end{eqnarray}
\] となるので，
\[
\begin{eqnarray}
R &=& \frac {V_{1}}{I_{1}} \\[ 5pt ] &=& \frac {10}{5} \\[ 5pt ] &=& 2 \ \mathrm { [ \Omega ] } \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ハ
$ \ r_{1} \ $と$ \ r_{2}+R \ $の合成抵抗は$ \ R \ $と等しいことから，
\[
\begin{eqnarray}
R &=& \frac {r_{1}\left( r_{2}+R\right) }{r_{1}+\left( r_{2}+R\right) } \\[ 5pt ] 2 &=& \frac {6\left( r_{2}+2\right) }{6+r_{2}+2} \\[ 5pt ] 2\left( r_{2}+8\right) &=& 6\left( r_{2}+2\right) \\[ 5pt ] r_{2} &=& 1 \ \mathrm { [ \Omega ] } \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：チ
分流比の関係から
\[
\begin{eqnarray}
I_{2} &=& \frac {r_{1} }{r_{1}+\left( r_{2}+R\right) }I_{1} \\[ 5pt ] &=& \frac {6 }{6+1+2}\times 5 \\[ 5pt ] &=& \frac {10}{3} \ \mathrm { [ A ] } \\[ 5pt ] \end{eqnarray}
\] と求められる。