《理論》〈電気回路〉[H29:問4]エアトン分流器を使った直流電流測定に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，エアトン分流器を使った直流電流測定に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

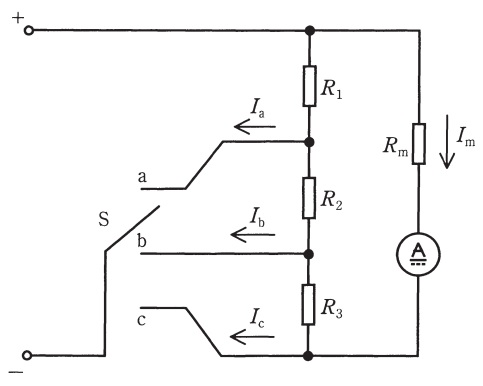
図は理想的な直流電流計に分流器を接続し，スイッチ$ \ \mathrm {S} \ $を切り替えることで直流電流の測定範囲を拡大する回路である。
図より，スイッチ$ \ \mathrm {S} \ $が位置$ \ \mathrm {a} \ $において，
\[
\left( \ \fbox {　（１）　} \ \right) I_{\mathrm {m}} =R_{1} \left( I_{\mathrm {a}}-I_{\mathrm {m}} \right) 　・・・・・・・・・・・・・・　①
\] スイッチ$ \ \mathrm {S} \ $が位置$ \ \mathrm {b} \ $において，
\[
\left( \ \fbox {　（２）　} \ \right) I_{\mathrm {m}} =\left( \ \fbox {　（３）　} \ \right) \left( I_{\mathrm {b}}-I_{\mathrm {m}} \right) 　・・・・・・・・・　②
\] スイッチ$ \ \mathrm {S} \ $が位置$ \ \mathrm {c} \ $において，
\[
R_{\mathrm {m}}I_{\mathrm {m}} =\left( \ \fbox {　（４）　} \ \right) \left( I_{\mathrm {c}}-I_{\mathrm {m}} \right) 　・・・・・・・・・・・・・・　③
\] が成立する。
ここで，$ \ R_{\mathrm {m}} \ $が$ \ 100 \ \Omega \ $，電流計に流れる電流$ \ I_{\mathrm {m}} \ $が$ \ 0.05 \ \mathrm {A} \ $であるとき，スイッチ$ \ \mathrm {S} \ $が位置$ \ \mathrm {a} \ $において電流$ \ I_{\mathrm {a}}=105 \ \mathrm {A} \ $，位置$ \ \mathrm {b} \ $において電流$ \ I_{\mathrm {b}}=10.5 \ \mathrm {A} \ $，位置$ \ \mathrm {c} \ $において電流$ \ I_{\mathrm {c}}=1.05 \ \mathrm {A} \ $を測定するものとする。$ \ R_{1}=0.05 \ \Omega \ $であるとき$ \ R_{3} \ $を求めれば，$ \ R_{3}=\fbox {　（５）　} \ \Omega \ $となる。

〔問4の解答群〕
\[
\begin{eqnarray}
&（イ）&　R_{3}+R_{\mathrm {m}}　　　&（ロ）&　R_{1}+R_{2}+R_{3}+R_{\mathrm {m}}　　　&（ハ）&　R_{2}+R_{\mathrm {m}} \\[ 5pt ] &（ニ）&　R_{1}+R_{2}　　　&（ホ）&　R_{1}+R_{2}+R_{\mathrm {m}}　　　&（ヘ）&　R_{2}+R_{3}+R_{\mathrm {m}} \\[ 5pt ] &（ト）&　0.45　　　&（チ）&　R_{1}+R_{\mathrm {m}}　　　&（リ）&　R_{1}+R_{3}+R_{\mathrm {m}} \\[ 5pt ] &（ヌ）&　4.50　　　&（ル）&　R_{1}+R_{2}+R_{3}　　　&（ヲ）&　4.95 \\[ 5pt ] &（ワ）&　R_{2}+R_{3}　　　&（カ）&　R_{\mathrm {m}}　　　&（ヨ）&　R_{1}+R_{3}
\end{eqnarray}
\]

【ワンポイント解説】

(1)～(4)までは基本的な回路計算の問題で，(5)は数値を代入し計算する問題です。(5)は解答では連立方程式を解いて解答を出していますが，試験本番では解答の選択肢から，数値を代入した時点で$ \ R_{2}≠4.95 \ $，$ \ R_{3}>R_{2} \ $と予想し，消去法で$（ヌ）4.50 \ $を推量できると時間も短縮され，計算ミスによる間違いも防げます。

【解答】

(1)解答：ヘ
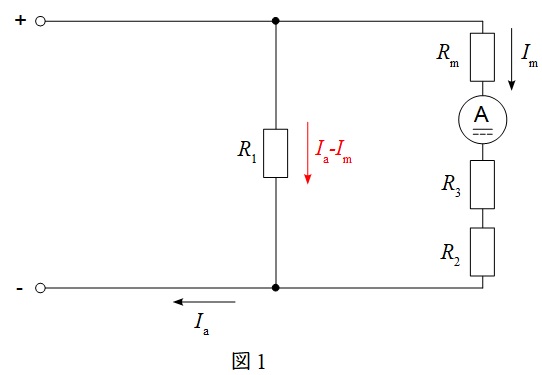
問題図のスイッチ$ \ \mathrm {S} \ $を位置$ \ \mathrm {a} \ $にした時の回路を整理すると，図1のようになる。
図1において，並列回路における分路の電圧降下は等しいから,
\[
\begin{eqnarray}
\left( R_{2}+R_{3}+R_{\mathrm {m}} \right) I_{\mathrm {m}}=R_{1} \left( I_{\mathrm {a}}-I_{\mathrm {m}} \right) \\[ 5pt ] \end{eqnarray}
\] となる。

(2)解答：イ
(3)解答：ニ
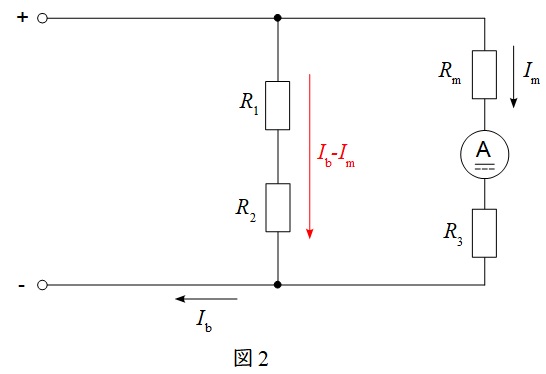
(1)と同様に問題図のスイッチ$ \ \mathrm {S} \ $を位置$ \ \mathrm {b} \ $にした時の回路を整理すると，図2のようになる。
図2において，並列回路における分路の電圧降下は等しいから,
\[
\begin{eqnarray}
\left( R_{3}+R_{\mathrm {m}} \right) I_{\mathrm {m}}=\left( R_{1}+R_{2}\right) \left( I_{\mathrm {b}}-I_{\mathrm {m}} \right) \\[ 5pt ] \end{eqnarray}
\] となる。

(4)解答：ル
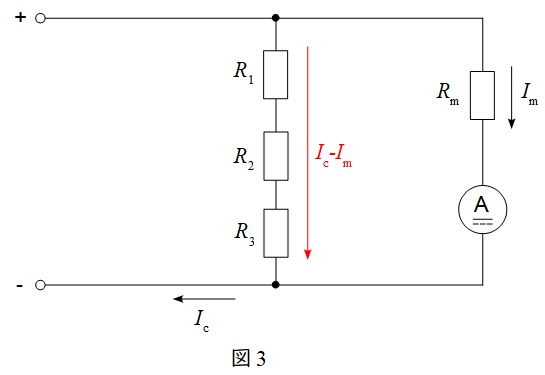
(1)，(2)と同様に問題図のスイッチ$ \ \mathrm {S} \ $を位置$ \ \mathrm {c} \ $にした時の回路を整理すると，図3のようになる。
図3において，並列回路における分路の電圧降下は等しいから,
\[
\begin{eqnarray}
R_{\mathrm {m}} I_{\mathrm {m}}=\left( R_{1}+R_{2}+R_{3}\right) \left( I_{\mathrm {c}}-I_{\mathrm {m}} \right) \\[ 5pt ] \end{eqnarray}
\] となる。

(5)解答：ヌ
①～③に$ \ R_{\mathrm {m}}=100 \ [\Omega] \ $，$ \ I_{\mathrm {m}}=0.05 \ \mathrm {[A]} \ $，$ \ I_{\mathrm {a}}=105 \ \mathrm {[A]} \ $，$ \ I_{\mathrm {b}}=10.5 \ \mathrm {[A]} \ $，$ \ I_{c}=1.05 \ \mathrm {[A]} \ $，$ \ R_{1}=0.05 \ [\Omega] \ $を代入すると，
\[
\begin{eqnarray}
\left( R_{2}+R_{3}+100 \right) \times 0.05 &=& 0.05 \times \left( 105-0.05 \right)　&　・・・　①^{\prime }& \\[ 5pt ] \left( R_{3}+100 \right) \times 0.05 &=& \left( 0.05+R_{2}\right) \left( 10.5-0.05 \right)　&　・・・　②^{\prime }& \\[ 5pt ] 100 \times 0.05 &=& \left( 0.05+R_{2}+R_{3}\right) \left( 1.05-0.05 \right) &　・・・　③^{\prime }& \\[ 5pt ] \end{eqnarray}
\] となり，それぞれ整理すると，
\[
\begin{eqnarray}
R_{2}+R_{3} &=& 4.95　&　・・・・・・・・・・・・・・・・・・・・　①^{\prime \prime}& \\[ 5pt ] 209R_{2}-R_{3} &=& 89.55　&　・・・・・・・・・・・・・・・・・・・・　②^{\prime\prime }& \\[ 5pt ] 4.95 &=& R_{2}+R_{3}　&　・・・・・・・・・・・・・・・・・・・・　③^{\prime\prime }& \\[ 5pt ] \end{eqnarray}
\] となる。$①^{\prime \prime}$と$③^{\prime \prime}$は全く同じ等式なので$①^{\prime \prime}$，$②^{\prime \prime}$のみで$ \ R_{3} \ $を導出すればよい。$①^{\prime \prime}+②^{\prime \prime}$より，
\[
\begin{eqnarray}
210R_{2}&=&94.5 \\[ 5pt ] R_{2}&=&0.45 \ [\Omega ] \\[ 5pt ] \end{eqnarray}
\] となり，$①^{\prime \prime}$より，$R_{3} =4.95-R_{2}$であるから，
\[
\begin{eqnarray}
R_{3} &=&4.95-0.45 \\[ 5pt ] &=&4.5 \ [\Omega ] \\[ 5pt ] \end{eqnarray}
\] と求められる。