《理論》〈電磁気〉[H30:問1]点電荷が真空中に作り出す電界に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，点電荷が真空中に作り出す電界に関する記述である。文中の$\fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$}$に当てはまる最も適切なものを解答群の中から選べ。なお，$\varepsilon _{0}$は真空の誘電率である。

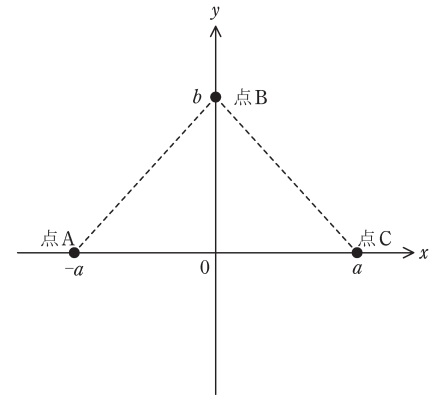
図のように$ \ xy \ $平面上に点$ \ \mathrm {A}$$ \left( x，y \right) =\left( -a，0 \right) $に電荷$ \ +Q \ $の点電荷を置く。この点電荷が$ \ y \ $軸上の点$ \ \mathrm {B}$$ \left( x，y \right) =\left( 0，b \right) $に作り出す電界の$ \ x \ $成分は$ \ \displaystyle \frac {Q}{4\pi \varepsilon _{0}}\times \fbox {　（１）　}$，$ \ y \ $成分は$ \ \displaystyle \frac {Q}{4\pi \varepsilon _{0}}\times \fbox {　（２）　}$となる。

さらに，点$ \ \mathrm {C}$$ \left( x，y \right) =\left( a，0 \right) $に電荷$ \ -Q \ $の点電荷を置いた場合には，点$ \ \mathrm {B}$における合成電界は$ \ x \ $成分のみをもち，$ \ b= \fbox {　（３）　}$の場合にその大きさが最大となる。

一方，点$ \ \mathrm {C}$に電荷$ \ +Q \ $の点電荷を置いた場合には，点$ \ \mathrm {B}$における合成電界は$ \ y \ $成分のみをもち，$ \ \displaystyle \frac {Q}{4\pi \varepsilon _{0}}\times \fbox {　（４）　}$となる。この合成電界は，$ \ b= \fbox {　（５）　}$の場合にその大きさが最大となる。

〔問1の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {a}{a^{2}+b^{2}}　　　&（ロ）&　\frac {a+b}{\left( a^{2}+b^{2}\right) ^{\frac {3}{2}}}　　　&（ハ）&　\frac {b}{a^{2}+b^{2}} \\[ 5pt ] &（ニ）&　±\frac {a}{2}　　　&（ホ）&　±a　　　&（ヘ）&　±2a \\[ 5pt ] &（ト）&　\frac {a}{\left( a^{2}+b^{2}\right) ^{\frac {3}{2}}}　　　&（チ）&　\frac {2a}{\left( a^{2}+b^{2}\right) ^{\frac {3}{2}}}　　　　&（リ）&　±\frac {a}{\sqrt {2}} \\[ 5pt ] &（ヌ）&　\frac {b}{\left( a^{2}+b^{2}\right) ^{\frac {1}{2}}}　　　&（ル）&　\frac {2b}{\left( a^{2}+b^{2}\right) ^{\frac {3}{2}}}　　　&（ヲ）&　±∞ \\[ 5pt ] &（ワ）&　\frac {b}{\left( a^{2}+b^{2}\right) ^{\frac {3}{2}}}　　　&（カ）&　\frac {a}{\left( a^{2}+b^{2}\right) ^{\frac {1}{2}}}　　　&（ヨ）&　0 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

(1)～(4)までは，比較的出題されやすく，難易度もそれほど高くありません。(5)は微分の計算があるので三種より高度な問題となります。

1.点電荷が作る電界の強さ$ \ E \ $
真空中で$ \ Q \ $が作る電界の大きさ$ \ E \ $は，距離$ \ r \ $の地点で，
\[
\begin{eqnarray}
E&=&\frac {Q}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

2.割り算の微分の公式
$ \ \displaystyle y=\frac {u(x)}{v(x)} \ $で示される関数の微分は，
\[
\begin{eqnarray}
\frac {\mathrm {d}y}{\mathrm {d}x}&=&\frac {u^{\prime }v-uv^{\prime }}{v^{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：ト
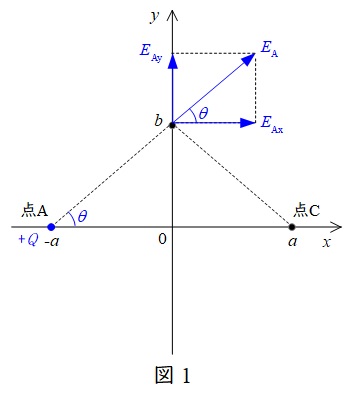
点$ \ \mathrm {A}$に$ \ +Q \ $の電荷を置いた時，点$ \ \mathrm {B}$にできる電界は図1のようになる。
ここで，$ \ \mathrm {AB}$間の距離$r$は，三平方の定理より，
\[
\begin{eqnarray}
r&=&\sqrt {a^{2} +b^{2}} \\[ 5pt ] \end{eqnarray}
\] であるから，点$ \ \mathrm {B}$にできる電界の大きさ$E_{\mathrm {A}}$は，ワンポイント解説「1.点電荷が作る電界の強さ$E$」より，
\[
\begin{eqnarray}
E_{\mathrm {A}}&=&\frac {Q}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ] &=&\frac {Q}{4\pi \varepsilon _{0}\left( a^{2} +b^{2}\right) } \\[ 5pt ] \end{eqnarray}
\] となり，その$x$成分は$\displaystyle \cos \theta =\frac {a}{\sqrt {a^{2} +b^{2}}}$より，
\[
\begin{eqnarray}
E_{\mathrm {Ax}}&=&E_{\mathrm {A}}\cos \theta \\[ 5pt ] &=&\frac {Q}{4\pi \varepsilon _{0}\left( a^{2} +b^{2}\right) }\cdot \frac {a}{\sqrt {a^{2} +b^{2}}} \\[ 5pt ] &=&\frac {Q}{4\pi \varepsilon _{0}}\times \frac {a}{\left( a^{2} +b^{2}\right) ^{\frac {3}{2}}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ワ
(1)と同様$y$成分は$\displaystyle \sin \theta =\frac {b}{\sqrt {a^{2} +b^{2}}}$より，
\[
\begin{eqnarray}
E_{\mathrm {Ay}}&=&E_{\mathrm {A}}\sin \theta \\[ 5pt ] &=&\frac {Q}{4\pi \varepsilon _{0}\left( a^{2} +b^{2}\right) }\cdot \frac {b}{\sqrt {a^{2} +b^{2}}} \\[ 5pt ] &=&\frac {Q}{4\pi \varepsilon _{0}}\times \frac {b}{\left( a^{2} +b^{2}\right) ^{\frac {3}{2}}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ヨ
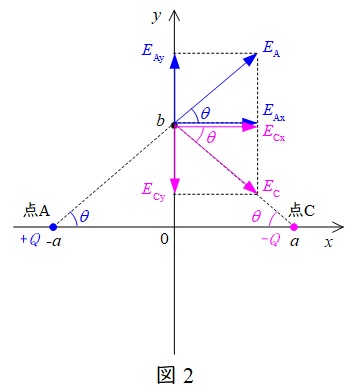
点$ \ \mathrm {C}$に$ \ -Q \ $の電荷を置いた時，点$ \ \mathrm {B}$にできる電界は図2のようになる。
図2より，$y$成分は打ち消され$ \ 0 \ $になる。また，$ \ E_{\mathrm {Ax}}=E_{\mathrm {Cx}} \ $より，$ \ x \ $成分の合計$ \ E_{\mathrm {x}} \ $は，
\[
\begin{eqnarray}
E_{\mathrm {x}}&=&E_{\mathrm {Ax}}+E_{\mathrm {Cx}} \\[ 5pt ] &=&\frac {Q}{4\pi \varepsilon _{0}}\times \frac {a}{\left( a^{2} +b^{2}\right) ^{\frac {3}{2}}}+\frac {Q}{4\pi \varepsilon _{0}}\times \frac {a}{\left( a^{2} +b^{2}\right) ^{\frac {3}{2}}} \\[ 5pt ] &=&\frac {Q}{2\pi \varepsilon _{0}}\times \frac {a}{\left( a^{2} +b^{2}\right) ^{\frac {3}{2}}} \\[ 5pt ] \end{eqnarray}
\] となる。$ \ E_{\mathrm {x}} \ $が最大となるのは，$ \ b=0 \ $の時で，
\[
\begin{eqnarray}
E_{\mathrm {x}}&=&\frac {Q}{2\pi \varepsilon _{0}}\times \frac {a}{\left( a^{2} +0\right) ^{\frac {3}{2}}} \\[ 5pt ] &=&\frac {Q}{2\pi \varepsilon _{0}a^{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ル
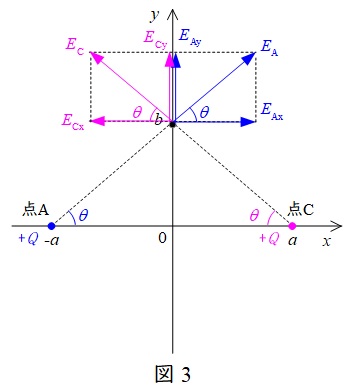
点$ \ \mathrm {C}$に$ \ +Q \ $の電荷を置いた時，点$ \ \mathrm {B}$にできる電界は図3のようになる。
図3より，$x$成分は打ち消され$ \ 0 \ $になる。また，$E_{\mathrm {Ay}}=E_{\mathrm {Cy}}$より，$y$成分の合計$E_{\mathrm {y}}$は，
\[
\begin{eqnarray}
E_{\mathrm {y}}&=&E_{\mathrm {Ay}}+E_{\mathrm {Cy}} \\[ 5pt ] &=&\frac {Q}{4\pi \varepsilon _{0}}\times \frac {b}{\left( a^{2} +b^{2}\right) ^{\frac {3}{2}}}+\frac {Q}{4\pi \varepsilon _{0}}\times \frac {b}{\left( a^{2} +b^{2}\right) ^{\frac {3}{2}}} \\[ 5pt ] &=&\frac {Q}{4\pi \varepsilon _{0}}\times \frac {2b}{\left( a^{2} +b^{2}\right) ^{\frac {3}{2}}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：リ
ワンポイント解説「2.割り算の微分の公式」より，(4)の解答式を微分すると，
\[
\begin{eqnarray}
\frac {\mathrm {d}E_{\mathrm {y}}}{\mathrm {d}b}&=&\frac {Q}{2\pi \varepsilon _{0}}\frac {\left( a^{2} +b^{2}\right) ^{\frac {3}{2}}-b\cdot 2b \cdot \frac {3}{2} \left( a^{2} +b^{2}\right) ^{\frac {1}{2}}}{\left( a^{2} +b^{2}\right) ^{3}} \\[ 5pt ] &=&\frac {Q}{2\pi \varepsilon _{0}}\frac {\left( a^{2} +b^{2}\right) ^{\frac {1}{2}}\left\{ \left( a^{2} +b^{2}\right) -3b^{2} \right\} }{\left( a^{2} +b^{2}\right) ^{3}} \\[ 5pt ] &=&\frac {Q}{2\pi \varepsilon _{0}}\frac {\left( a^{2} +b^{2}\right) ^{\frac {1}{2}}\left( a^{2} -2b^{2}\right) }{\left( a^{2} +b^{2}\right) ^{3}} \\[ 5pt ] \end{eqnarray}
\] となる。（詳細計算方法はこちら）$E_{\mathrm {y}}$が最大となる点は$\displaystyle \frac {\mathrm {d}E_{\mathrm {y}}}{\mathrm {d}b}=0$となる点であるから，
\[
\begin{eqnarray}
\frac {Q}{2\pi \varepsilon _{0}}\frac {\left( a^{2} +b^{2}\right) ^{\frac {1}{2}}\left( a^{2} -2b^{2}\right) }{\left( a^{2} +b^{2}\right) ^{3}} &=&0 \\[ 5pt ] a^{2} -2b^{2}&=& 0 \\[ 5pt ] b&=&±\frac {a}{\sqrt {2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。