《理論》〈電気回路〉[R01:問3]キャパシタ及び抵抗の並列回路における過渡現象に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，電気回路の過渡現象に関する記述である。文中の$\ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

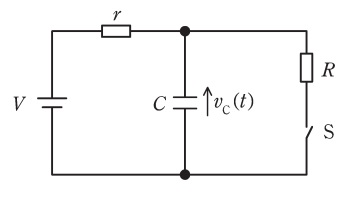
図の回路は，時刻$\ t＜0 \ $において，スイッチ$\ \mathrm {S} \ $は開いており，回路は定常状態にある。この回路のスイッチ$\ \mathrm {S} \ $を$\ t=0 \ $で閉じるものとする。

スイッチ$\ \mathrm {S} \ $を閉じた後，十分に時間が経過して回路が定常状態になったときのキャパシタ$\ C \ $の電圧は，$\ \fbox {　 （１） 　} \ $である。したがって，時刻$\ t=0 \ $でスイッチ$\ \mathrm {S} \ $を閉じた後の過渡状態においては，回路の時定数を$\ T_{1} \ $とすれば，キャパシタ$\ C \ $の電圧は，

$$\begin{eqnarray} v_{\mathrm {C}}\left( t\right) &=&\fbox {　 （１） 　} \ + \ \fbox {　 （２） 　} \ \mathrm {e}^{-\frac {t}{T_{1}}}，\left( t≧0\right) \\[ 5pt ] \end{eqnarray}$$ となる。ここで回路の時定数は，$\ T_{1}=\fbox {　 （３） 　} \ $である。

スイッチ$\ \mathrm {S} \ $を閉じた後，十分に時間が経過して回路が定常状態になった時刻$\ t=t_{0} \ $で，再びスイッチ$\ \mathrm {S} \ $を開いた。スイッチ$\ \mathrm {S} \ $を再び開いた後の過渡状態においては，回路の時定数を$\ T_{2} \ $とすれば，キャパシタ$\ C \ $の電圧は，

$$\begin{eqnarray} v_{\mathrm {C}}\left( t\right) &=&\fbox {　 （１） 　} \ + \ \fbox {　 （２） 　} \ \left( \ \fbox {　 （４） 　} \ \right) ，\left( t≧t_{0}\right) \\[ 5pt ] \end{eqnarray}$$ となる。ここで回路の時定数は，$\ T_{2}=\fbox {　 （５） 　} \ $である。

〔問3の解答群〕

$$\begin{eqnarray} &（イ）&　V　　　&（ロ）&　\frac {r}{R+r}V　　　&（ハ）&　1-\mathrm {e}^{-\left( t-t_{0}\right) ／T_{2}} \\[ 5pt ] &（ニ）&　\frac {R}{R+r}V　　　&（ホ）&　0　　　&（ヘ）&　\frac {R+r}{r}V \\[ 5pt ] &（ト）&　\frac {CRr}{R+r}　　　&（チ）&　C\left( R+r\right)　　　　&（リ）&　1+\mathrm {e}^{-\left( t-t_{0}\right) ／T_{2}} \\[ 5pt ] &（ヌ）&　\frac {C}{r}　　　&（ル）&　\frac {r}{C}　　　&（ヲ）&　-1+\mathrm {e}^{-\left( t-t_{0}\right) ／T_{2}} \\[ 5pt ] &（ワ）&　-\frac {R}{R+r}V　　　&（カ）&　Cr　　　&（ヨ）&　\frac {R+r}{CRr} \\[ 5pt ] \end{eqnarray}$$

【ワンポイント解説】

電験2種では定番となっている過渡現象に関する問題です。近年は$\ RL \ $や$\ RC \ $直列回路といったストレートな問題は少なくなってきている印象があります。本問も手計算では比較的時間がかかる問題となります。電圧がどのように変化するかある程度予想して，その中で解答式が分かるとグッと短時間で解けるようになると思います。

1.過渡現象における$\ RLC \ $それぞれの電圧
線路に流れる電流を$\ i \ $とし，抵抗$\ R \ $の電圧$\ V_{\mathrm{R}} \ $，リアクトル$\ L \ $の電圧$\ V_{\mathrm{L}} \ $，コンデンサ$\ C \ $の電圧$\ V_{\mathrm{C}} \ $とすると，

$$\begin{eqnarray} V_{\mathrm{R}} &=& Ri \\[ 5pt ] V_{\mathrm{L}} &=& L\frac {\mathrm {d}i}{\mathrm {d}t} \\[ 5pt ] V_{\mathrm{C}} &=& \frac {1}{C}\int i \mathrm {d}t \\[ 5pt ] \end{eqnarray}$$ となり，電荷$\ q \ $との間に$\ \displaystyle i=\frac {\mathrm {d}q}{\mathrm {d}t} \ $の関係があるので，
$$\begin{eqnarray} V_{\mathrm{R}} &=& R\frac {\mathrm {d}q}{\mathrm {d}t} \\[ 5pt ] V_{\mathrm{L}} &=& L\frac {\mathrm {d}^{2}q}{\mathrm {d}t^{2}} \\[ 5pt ] V_{\mathrm{C}} &=& \frac {q}{C} \end{eqnarray}$$ となります。

2.過渡現象における定常解と過渡解
ⅰ．定常解を$\ i_{\mathrm {s}} \ $，過渡解を$\ i_{\mathrm {t}} \ $とすると，電流値$\ i \ $は$\ i=i_{\mathrm {s}}+i_{\mathrm {t}} \ $となります。
ⅱ．定常解は電流の時間変化のない状態すなわち$\ \displaystyle \frac {\mathrm {d}i_{\mathrm {s}}}{\mathrm {d}t}=0 \ $とした時の解です。
ⅲ．過渡解はスイッチを入れた直後の解すなわち$\ L \ $開放($\ E=0 \ $と同義)の時の解です。

3.自然対数の微分積分
①自然対数の微分

$$\begin{eqnarray} \frac {\mathrm {d}}{\mathrm {d}x} \left( \ln {x}\right) &=&\frac {1}{x}　\\[ 5pt ] \end{eqnarray}$$ ②自然対数の積分
$$\begin{eqnarray} \int \frac {1}{x} \mathrm {d}x &=&\ln {x} + C \left( Cは積分定数\right)　\\[ 5pt ] \end{eqnarray}$$ となり，
$$\begin{eqnarray} \ln {x}&=&-\alpha t +C \left( Cは積分定数\right) \\[ 5pt ] \end{eqnarray}$$ となった場合，両辺とも対数を外すと，
$$\begin{eqnarray} x&=&A\mathrm {e}^{-\alpha t} \left( A=e^{C}\right) \\[ 5pt ] \end{eqnarray}$$ となります。

【関連する「電気の神髄」記事】

　　RC並列回路の過渡現象（直流回路）

【解答】

(1)解答：ニ
$\ \mathrm {S} \ $を閉じた後，十分に時間が経過して回路が定常状態になると$\ C \ $には電流が流れないので，$\ C \ $の電圧は$\ R \ $の電圧と等しくなる。したがって，分圧の法則より，定常状態におけるキャパシタの電圧$\ v_{\mathrm {Cs1}} \ $は，

$$\begin{eqnarray} v_{\mathrm {Cs1}}&=&\frac {R}{R+r}V \\[ 5pt ] \end{eqnarray}$$ となる。

(2)解答：ロ
スイッチ$\ \mathrm {S} \ $を閉じた後の回路方程式は，$\ r \ $に流れる電流を$\ i \ $，$\ C \ $に流れる電流を$\ i_{\mathrm {C}} \ $，$\ R \ $に流れる電流を$\ i_{\mathrm {R}} \ $とすると，

$$\begin{eqnarray} ri+\frac {1}{C}\int i_{\mathrm {C}} \mathrm {d}t &=&V　&・・・・・・・・・　①& \\[ 5pt ] \frac {1}{C}\int i_{\mathrm {C}}\mathrm {d}t &=&Ri_{\mathrm {R}}　&・・・・・・・・・　②& \\[ 5pt ] i &=&i_{\mathrm {C}}+i_{\mathrm {R}}　&・・・・・・・・・　③& \\[ 5pt ] \end{eqnarray}$$ であるから，③，②の順に①に代入して整理すると，
$$\begin{eqnarray} r\left( i_{\mathrm {C}}+i_{\mathrm {R}}\right) +\frac {1}{C}\int i_{\mathrm {C}} \mathrm {d}t &=&V \\[ 5pt ] r\left( i_{\mathrm {C}}+\frac {1}{CR}\int i_{\mathrm {C}}\mathrm {d}t\right) +\frac {1}{C}\int i_{\mathrm {C}}\mathrm {d}t &=&V \\[ 5pt ] ri_{\mathrm {C}}+\frac {R+r}{CR}\int i_{\mathrm {C}}\mathrm {d}t &=&V \\[ 5pt ] \end{eqnarray}$$ となる。ワンポイント解説「1.過渡現象における$\ RLC \ $それぞれの電圧」の通り，コンデンサに蓄えられる電荷$\ q_{\mathrm {C}} \ $との間に$\ \displaystyle i_{\mathrm {C}}=\frac {\mathrm {d}q_{\mathrm {C}}}{\mathrm {d}t} \ $の関係があるので，
$$\begin{eqnarray} r\frac {\mathrm {d}q_{\mathrm {C}}}{\mathrm {d}t}+\frac {R+r}{CR}q_{\mathrm {C}} &=&V \\[ 5pt ] \end{eqnarray}$$ となる。ワンポイント解説「2.過渡現象における定常解と過渡解」に沿って，定常解を$\ q_{\mathrm {Cs}} \ $，過渡解を$\ q_{\mathrm {Ct}} \ $とする。定常状態においては，$\ \displaystyle \frac {\mathrm {d}q_{\mathrm {C}}}{\mathrm {d}t}=0 \ $であるから，
$$\begin{eqnarray} \frac {R+r}{CR}q_{\mathrm {Cs}} &=&V \\[ 5pt ] q_{\mathrm {Cs}} &=&\frac {CR}{R+r}V \\[ 5pt ] \end{eqnarray}$$ となる。また，過渡状態においては，$\ V=0 \ $とすると，
$$\begin{eqnarray} r\frac {\mathrm {d}q_{\mathrm {Ct}}}{\mathrm {d}t}+\frac {R+r}{CR}q_{\mathrm {Ct}} &=&0 \\[ 5pt ] r\frac {\mathrm {d}q_{\mathrm {Ct}}}{\mathrm {d}t} &=&-\frac {R+r}{CR}q_{\mathrm {Ct}} \\[ 5pt ] \frac {1}{q_{\mathrm {Ct}}}\mathrm {d}q_{\mathrm {Ct}} &=&-\frac {R+r}{CRr}\mathrm {d}t \\[ 5pt ] q_{\mathrm {Ct}} &=&A\mathrm {e}^{-\frac {R+r}{CRr}t}　\left( Aは積分定数\right) \\[ 5pt ] \end{eqnarray}$$ となる。よって，一般解$\ q_{\mathrm {C}} \ $は，
$$\begin{eqnarray} q_{\mathrm {C}} &=&q_{\mathrm {Cs}}+q_{\mathrm {Ct}} \\[ 5pt ] &=&\frac {CR}{R+r}V+A\mathrm {e}^{-\frac {R+r}{CRr}t} \\[ 5pt ] \end{eqnarray}$$ となる。$\ t=0 \ $において$\ q_{\mathrm {C}}=CV \ $であるから，
$$\begin{eqnarray} CV &=&\frac {CR}{R+r}V+A \\[ 5pt ] A&=&\frac {Cr}{R+r}V \\[ 5pt ] \end{eqnarray}$$ となり，
$$\begin{eqnarray} q_{\mathrm {C}} &=&\frac {CR}{R+r}V+\frac {Cr}{R+r}V\mathrm {e}^{-\frac {R+r}{CRr}t} \\[ 5pt ] \end{eqnarray}$$ となる。よって，$\ v_{\mathrm {C}}\left( t \right) \ $は，
$$\begin{eqnarray} v_{\mathrm {C}}\left( t \right) &=&\frac {q_{\mathrm {C}}}{C} \\[ 5pt ] &=&\frac {R}{R+r}V+\frac {r}{R+r}V\mathrm {e}^{-\frac {R+r}{CRr}t} \\[ 5pt ] \end{eqnarray}$$ と求められる。

(3)解答：ト
(2)の解答式より，時定数$\ T_{1} \ $は，$\ \displaystyle T_{1}=\frac {CRr}{R+r} \ $と求められる。

(4)解答：ハ
スイッチを開いた後の回路方程式は，

$$\begin{eqnarray} ri+\frac {1}{C}\int i \mathrm {d}t &=&V \\[ 5pt ] \end{eqnarray}$$ すなわち，
$$\begin{eqnarray} r\frac {\mathrm {d}q}{\mathrm {d}t}+\frac {q}{C} &=&V \\[ 5pt ] \end{eqnarray}$$ の関係があるので，定常解を$\ q_{\mathrm {s}} \ $，過渡解を$\ q_{\mathrm {t}} \ $とすると，定常状態においては，$\ \displaystyle \frac {\mathrm {d}q}{\mathrm {d}t}=0 \ $であるから，
$$\begin{eqnarray} \frac {q_{\mathrm {s}}}{C} &=&V \\[ 5pt ] q_{\mathrm {s}} &=&CV \\[ 5pt ] \end{eqnarray}$$ となる。また，過渡状態においては，$\ V=0 \ $とすると，
$$\begin{eqnarray} r\frac {\mathrm {d}q_{\mathrm {t}}}{\mathrm {d}t}+\frac {q_{\mathrm {t}}}{C} &=&0 \\[ 5pt ] \frac {1}{q_{\mathrm {t}}}\mathrm {d}q_{\mathrm {t}} &=&-\frac {1}{Cr}\mathrm {d}t \\[ 5pt ] q_{\mathrm {t}} &=&B\mathrm {e}^{-\frac {1}{Cr}t}　\left( Bは積分定数\right) \\[ 5pt ] \end{eqnarray}$$ となり，一般解は，
$$\begin{eqnarray} q &=&q_{\mathrm {s}}+q_{\mathrm {t}} \\[ 5pt ] &=&CV+B\mathrm {e}^{-\frac {1}{Cr}t} \\[ 5pt ] \end{eqnarray}$$ となる。$\ t=t_{0} \ $において，$\ \displaystyle q\left( t_{0} \right) =\frac {CR}{R+r}V \ $であるから，
$$\begin{eqnarray} \frac {CR}{R+r}V&=&CV+B\mathrm {e}^{-\frac {1}{Cr}t_{0}} \\[ 5pt ] B\mathrm {e}^{-\frac {1}{Cr}t_{0}}&=&\frac {CR}{R+r}V-CV \\[ 5pt ] &=&-\frac {Cr}{R+r}V \\[ 5pt ] B&=&-\frac {Cr}{R+r}V\mathrm {e}^{\frac {1}{Cr}t_{0}} \\[ 5pt ] \end{eqnarray}$$ となるので，
$$\begin{eqnarray} q &=&CV-\frac {Cr}{R+r}V\mathrm {e}^{\frac {1}{Cr}t_{0}}\mathrm {e}^{-\frac {1}{Cr}t} \\[ 5pt ] &=&CV-\frac {Cr}{R+r}V\mathrm {e}^{-\frac {1}{Cr}\left( t-t_{0}\right) } \\[ 5pt ] \end{eqnarray}$$ となる。よって，コンデンサ電圧$\ v_{\mathrm {C}}\left( t \right) \ $は，
$$\begin{eqnarray} v_{\mathrm {C}}\left( t \right) &=&\frac {q}{C} \\[ 5pt ] &=&V-\frac {r}{R+r}V\mathrm {e}^{-\frac {1}{Cr}\left( t-t_{0}\right) } \\[ 5pt ] &=&\frac {R}{R+r}V+\frac {r}{R+r}V-\frac {r}{R+r}V\mathrm {e}^{-\frac {1}{Cr}\left( t-t_{0}\right) } \\[ 5pt ] &=&\frac {R}{R+r}V+\frac {r}{R+r}V\left( 1-\mathrm {e}^{-\frac {1}{Cr}\left( t-t_{0}\right) }\right) \\[ 5pt ] \end{eqnarray}$$ と求められる。

(5)解答：カ
(4)の解答式より，時定数$\ T_{2} \ $は，$\ \displaystyle T_{2}=Cr \ $と求められる。

【本問に関する質疑応答】

　　コンデンサ電圧と放電
　　コンデンサが充電されないのはなぜ？
　　回路方程式は時間によって変わらない