《理論》〈電気及び電子計測〉[R03:問8]ブリッジの平衡条件を利用した静電容量の測定に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，交流ブリッジによるコンデンサの測定に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。

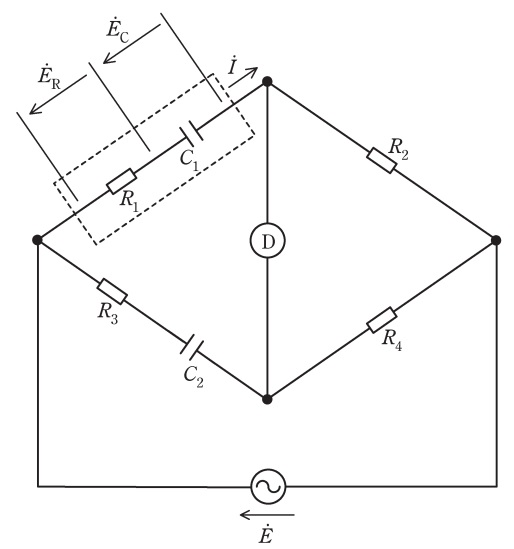
図の破線で囲んだ部分は測定対象のコンデンサで，その等価回路は静電容量\( \ C_{1} \ \)と抵抗\( \ R_{1} \ \)の直列回路である。図の\( \ R_{2} \ \)，\( \ R_{3} \ \)及び\( \ R_{4} \ \)は既知の抵抗，\( \ C_{2} \ \)は既知の静電容量，Ⓓは検出器である。また，交流電源の電圧を\( \ \dot E \ \)，その角周波数を\( \ \omega \ \)とする。

今，検出器の指示が零となりブリッジが平衡したとすると，次式が成り立つ。
\[
\begin{eqnarray}
\ \fbox {　 （１） 　} \ \\[ 5pt ] \end{eqnarray}
\] 上式から，\( \ R_{1}= \ \fbox {　 （２） 　} \ \)，\( \ C_{1}= \ \fbox {　 （３） 　} \ \)が求められる。

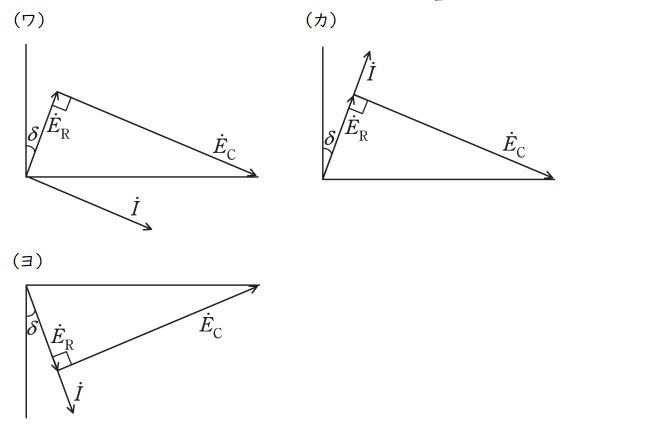
電圧\( \ {\dot E}_{\mathrm {R}} \ \)，電圧\( \ {\dot E}_{\mathrm {C}} \ \)及び電流\( \ \dot I \ \)をフェーザ図で表すと\( \ \fbox {　 （４） 　} \ \)となる。

フェーザ図に記した\( \ \delta \ \)の正接である\( \ \tan \delta = \ \fbox {　 （５） 　} \ \)は誘電正接と呼ばれ，コンデンサの性能を表す指標の一つである。なお，理想的なコンデンサの誘電正接は零となる。

〔問8の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {R_{4}}{R_{2}R_{3}}　　　　　&（ロ）&　\omega C_{2}R_{3}　　　　　&（ハ）&　\frac {C_{2}R_{2}}{R_{4}} \\[ 5pt ] &（ニ）&　\frac {R_{3}R_{4}}{R_{2}}　　　　　&（ホ）&　\frac {R_{3}}{\omega C_{2}}　　　　　&（ヘ）&　\frac {C_{2}R_{4}}{R_{2}} \\[ 5pt ] &（ト）&　\frac {R_{2}R_{3}}{R_{4}}　　　　　&（チ）&　\frac {1}{\omega C_{2}R_{3}}　　　　　&（リ）&　\frac {R_{2}}{C_{2}R_{4}} \\[ 5pt ] \end{eqnarray}
\] \[
\begin{eqnarray}
&（ヌ）&　\left( R_{1}+\frac {1}{\mathrm {j}\omega C_{1}}\right) R_{4} =\left( R_{3}+\frac {1}{\mathrm {j}\omega C_{2}}\right) R_{2} \\[ 5pt ] &（ル）&　R_{1}+R_{2}+\frac {1}{\mathrm {j}\omega C_{1}}=R_{3}+R_{4}+\frac {1}{\mathrm {j}\omega C_{2}} \\[ 5pt ] &（ヲ）&　\left( R_{1}+\frac {1}{\mathrm {j}\omega C_{1}}\right) R_{2} =\left( R_{3}+\frac {1}{\mathrm {j}\omega C_{2}}\right) R_{4} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

交流ブリッジのうち，コンデンサの静電容量を求めるためのシェーリングブリッジに関する問題です。
ブリッジの名称は様々ありますが，使用するのは同じ平衡条件の公式なので，確実に理解しておくようにしましょう。

1.抵抗，コイル，コンデンサの電圧\( \ V \ \mathrm {[V]} \ \)と電流\( \ I \ \mathrm {[A]} \ \)の関係
抵抗\( \ R \ \mathrm {[\Omega ]} \ \)，コイル\( \ L \ \mathrm {[H]} \ \)，コンデンサ\( \ C \ \mathrm {[F]} \ \)があり，角周波数が\( \ \omega \ \mathrm {[rad/s]} \ \)であるとき，それぞれのインピーダンスは，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {R}}&=&R \\[ 5pt ] {\dot Z}_{\mathrm {L}}&=&\mathrm {j}\omega L \\[ 5pt ] {\dot Z}_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C} \\[ 5pt ] \end{eqnarray}
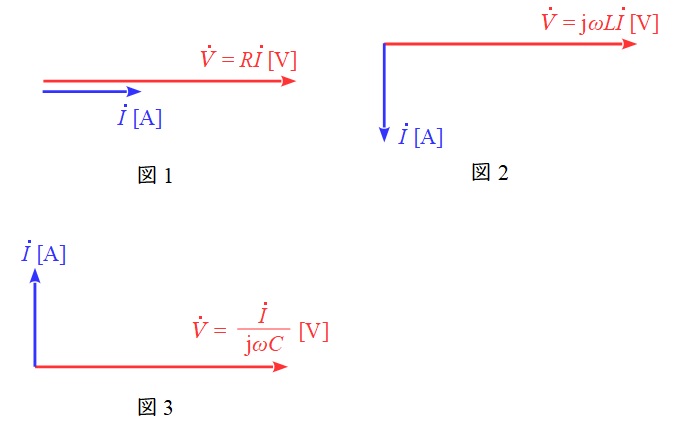
\] で求められ，それぞれの電圧と電流の関係は，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {R}}&=&R\dot I \\[ 5pt ] {\dot V}_{\mathrm {L}}&=&\mathrm {j}\omega L \dot I \\[ 5pt ] {\dot V}_{\mathrm {C}}&=&\frac {\dot I }{\mathrm {j}\omega C} \\[ 5pt ] \end{eqnarray}
\] となります。この関係をベクトル図に表すと，図1～図3となります。

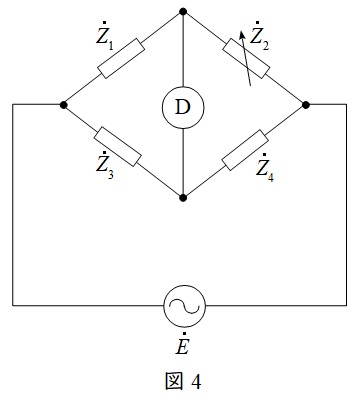
2.交流ブリッジ回路の平衡条件
図4の回路において，検流計Ⓓに電流が流れないようにしたとき，各インピーダンスの関係は，
\[
\begin{eqnarray}
{\dot Z}_{1}{\dot Z}_{4}&=&{\dot Z}_{2}{\dot Z}_{3} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：ヌ
ワンポイント解説「2.交流ブリッジ回路の平衡条件」の通り，ブリッジが平衡したとき，各インピーダンスの関係は，
\[
\begin{eqnarray}
\left( R_{1}+\frac {1}{\mathrm {j}\omega C_{1}}\right) R_{4}&=&\left( R_{3}+\frac {1}{\mathrm {j}\omega C_{2}}\right) R_{2} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ト
(1)の解答式を整理すると，
\[
\begin{eqnarray}
R_{1}R_{4}+\frac {R_{4}}{\mathrm {j}\omega C_{1}}&=&R_{2}R_{3}+\frac {R_{2}}{\mathrm {j}\omega C_{2}} \\[ 5pt ] R_{1}R_{4}-\mathrm {j}\frac {R_{4}}{\omega C_{1}}&=&R_{2}R_{3}-\mathrm {j}\frac {R_{2}}{\omega C_{2}}　・・・・・・・・・・　① \\[ 5pt ] \end{eqnarray}
\] となり，①式が成立するためには，実部と虚部がそれぞれ等しくなければならないので，実部を比較すると，
\[
\begin{eqnarray}
R_{1}R_{4}&=&R_{2}R_{3} \\[ 5pt ] R_{1}&=&\frac {R_{2}R_{3}}{R_{4}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ヘ
①式について，虚部を比較すると，
\[
\begin{eqnarray}
\frac {R_{4}}{\omega C_{1}}&=&\frac {R_{2}}{\omega C_{2}} \\[ 5pt ] \frac {R_{4}}{C_{1}}&=&\frac {R_{2}}{C_{2}} \\[ 5pt ] C_{1}&=&\frac {C_{2}R_{4}}{R_{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：カ
ワンポイント解説「1.抵抗，コイル，コンデンサの電圧\( \ V \ \mathrm {[V]} \ \)と電流\( \ I \ \mathrm {[A]} \ \)の関係」の通り，\( \ {\dot E}_{\mathrm {R}} \ \)は電流\( \ \dot I \ \)と同相，\( \ {\dot E}_{\mathrm {C}} \ \)は電流\( \ \dot I \ \)より\( \ \displaystyle \frac {\pi }{2} \ \mathrm {[rad]} \ \)遅れとなるので，これを満たすフェーザ図は（カ）である。

(5)解答：ロ
フェーザ図より，\( \ \tan \delta \ \)は，
\[
\begin{eqnarray}
\tan \delta &=&\frac {\left| {\dot E}_{\mathrm {R}}\right| }{\left| {\dot E}_{\mathrm {C}}\right| } \\[ 5pt ] &=&\frac {\left| R_{1}\dot I\right| }{\displaystyle \left| \frac {1}{\mathrm {j}\omega C_{1}}\dot I \right| } \\[ 5pt ] &=&\frac {\left| R_{1}\right| }{\displaystyle \left| \frac {1}{\mathrm {j}\omega C_{1}}\right| } \\[ 5pt ] &=&\frac {R_{1}}{\displaystyle \frac {1}{\omega C_{1}}} \\[ 5pt ] &=&\omega C_{1}R_{1} \\[ 5pt ] &=&\omega \frac {C_{2}R_{4}}{R_{2}}\frac {R_{2}R_{3}}{R_{4}} \\[ 5pt ] &=&\omega C_{2}R_{3} \\[ 5pt ] \end{eqnarray}
\] と求められる。