《理論》〈電気回路〉[R05:問3]二端子対抵抗回路の考え方に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★☆☆☆☆（易しい）

次の文章は，二端子対抵抗回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

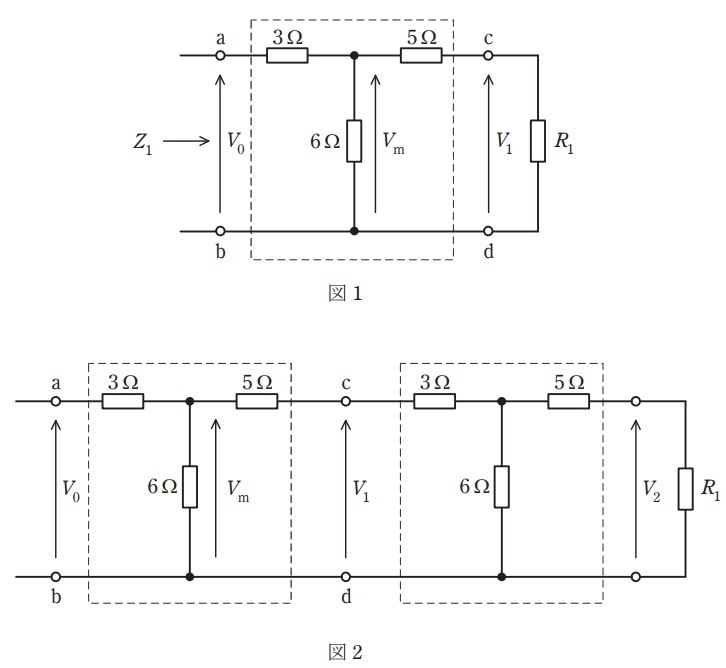
図1に示すように，二次側が抵抗$ \ R_{1} \ $で終端された$ \ 3 \ \mathrm {\Omega } \ $，$ \ 6 \ \mathrm {\Omega } \ $，$ \ 5 \ \mathrm {\Omega } \ $の抵抗からなる$ \ \mathrm {T} \ $形二端子対回路を考える。端子対$ \ \mathrm {a – b} \ $間の電圧を$ \ V_{0} \ $，端子対$ \ \mathrm {c – d} \ $間の電圧を$ \ V_{1} \ $，$ \ 6 \ \mathrm {\Omega } \ $の抵抗に掛かる電圧を$ \ V_{\mathrm {m}} \ $とする。$ \ R_{1}=7 \ \mathrm {\Omega } \ $のとき，端子対$ \ \mathrm {a – b} \ $から二次側を見たときのインピーダンスを$ \ Z_{1} \ $とすると，$ \ Z_{1} = \ \fbox {　（１）　} \ $，$ \ \displaystyle \frac {V_{\mathrm {m}}}{V_{0}} = \ \fbox {　（２）　} \ $，$ \ \displaystyle \frac {V_{1}}{V_{\mathrm {m}}} = \ \fbox {　（３）　} \ $となる。

次に，図2に示すように，図1の$ \ \mathrm {T} \ $形二端子対回路を二段縦続接続して図1と同じ抵抗$ \ R_{1} \ $で終端した回路を考える。$ \ R_{1}=7 \ \mathrm {\Omega } \ $のとき，$ \ R_{1} \ $に掛かる電圧を$ \ V_{2} \ $とすると，図2の回路の端子対$ \ \mathrm {a – b} \ $並びに端子対$ \ \mathrm {c – d} \ $から二次側を見たときのインピーダンスはいずれも図1の$ \ Z_{1} \ $と等しいので $ \ \displaystyle \frac {V_{1}}{V_{0}} =\frac {V_{2}}{V_{1}} \ $が成立し，$ \ \displaystyle \frac {V_{2}}{V_{0}} = \ \fbox {　（４）　} \ $となる。このとき，図2の抵抗$ \ R_{1}=7 \ \mathrm {\Omega } \ $で消費する電力は$ \ V_{0} \ $を使って表すと$ \ \fbox {　（５）　} \ \mathrm {[W]} \ $となる。

〔問3の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {7}{12}　　　　　&（ロ）&　\frac {4}{7}　　　　　&（ハ）&　\frac {V_ {0}^{2}}{163} \\[ 5pt ] &（ニ）&　\frac {1}{3^{2}}　　　　　&（ホ）&　\frac {1}{2^{2}}　　　　　&（ヘ）&　\frac {1}{4^{2}} \\[ 5pt ] &（ト）&　\frac {V_ {0}^{2}}{567}　　　　　&（チ）&　\frac {V_ {0}^{2}}{112}　　　　　&（リ）&　\frac {3}{7} \\[ 5pt ] &（ヌ）&　\frac {5}{7}　　　　　&（ル）&　4 \ \Omega　　　　　&（ヲ）&　5 \ \Omega \\[ 5pt ] &（ワ）&　\frac {11}{12}　　　　　&（カ）&　\frac {5}{12}　　　　　&（ヨ）&　7 \ \Omega \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

二端子対抵抗回路に関する問題です。
合成抵抗や分圧の法則を理解していれば，十分に完答を狙える問題であり，合格のためには是非とも完答したい問題となります。文章を読み解き，計算間違いに注意しながら解いていくようにして下さい。

1.合成抵抗
抵抗$ \ R_{1} \ \mathrm {[\Omega ]} \ $と$ \ R_{2} \ \mathrm {[\Omega ]} \ $が与えられている時，それぞれの合成抵抗$ \ R \ \mathrm {[\Omega ]} \ $は以下の式で与えられます。

①直列
直列合成抵抗$ \ R \ \mathrm {[\Omega ]} \ $は，
\[
\begin{eqnarray}
R&=&R_{1}+R_{2} \\[ 5pt ] \end{eqnarray}
\] となります。

②並列
並列合成抵抗$ \ R \ \mathrm {[\Omega ]} \ $は，
\[
\begin{eqnarray}
\frac {1}{R}&=&\frac {1}{R_{1}}+\frac {1}{R_{2}} \\[ 5pt ] \end{eqnarray}
\] となり，整理すると，
\[
\begin{eqnarray}
R&=&\frac {R_{1}R_{2}}{R_{1}+R_{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

2.分圧・分流の法則
①分圧の法則
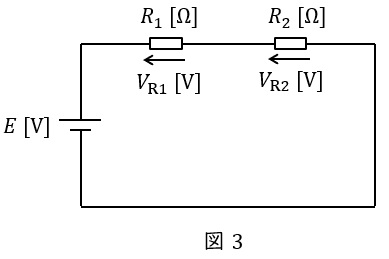
図3に示した直列回路において，各抵抗にかかる電圧は以下の通りとなります。
\[
\begin{eqnarray}
V_{\mathrm {R1}}&=&\frac {R_{1}}{R_{1}+R_{2}}E \\[ 5pt ] V_{\mathrm {R2}}&=&\frac {R_{2}}{R_{1}+R_{2}}E \\[ 5pt ] \end{eqnarray}
\]

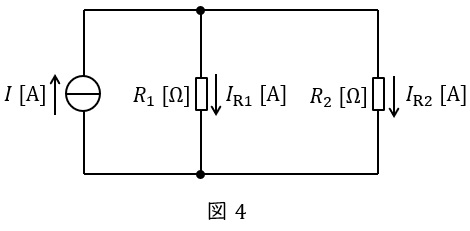
②分流の法則
図4に示した並列回路において，各抵抗に流れる電流は以下の通りとなります。分子の抵抗が分圧の法則と逆となることに注意して下さい。
\[
\begin{eqnarray}
I_{\mathrm {R1}}&=&\frac {\color{red}{R_{2}}}{R_{1}+R_{2}}I \\[ 5pt ] I_{\mathrm {R2}}&=&\frac {\color{red}{R_{1}}}{R_{1}+R_{2}}I \\[ 5pt ] \end{eqnarray}
\]

3.抵抗での消費電力
ある抵抗$ \ R \ \mathrm {[\Omega ]} \ $に電圧$ \ V \ \mathrm {[V]} \ $をかけたとき，抵抗に電流$ \ I \ \mathrm {[A]} \ $が流れたとすると，$ \ R \ \mathrm {[\Omega ]} \ $での消費電力$ \ P \ \mathrm {[W]} \ $は，
\[
\begin{eqnarray}
P &=&VI \\[ 5pt ] \end{eqnarray}
\] となります。オームの法則$ \ V=RI \ $より上式は，
\[
\begin{eqnarray}
P &=&RI^{2} \\[ 5pt ] &=&\frac {V^{2}}{R} \\[ 5pt ] \end{eqnarray}
\] と変形できます。

【解答】

(1)解答：ヨ
$ \ R_{1}=7 \ \mathrm {[\Omega ]} \ $と$ \ 5 \ \mathrm {\Omega } \ $が直列に接続され，さらに$ \ 6 \ \mathrm {\Omega } \ $が並列に接続されているので，その合成抵抗$ \ R_{\mathrm {m}} \ \mathrm {[\Omega ]} \ $は，ワンポイント解説「1.合成抵抗」の通り，
\[
\begin{eqnarray}
R_{\mathrm {m}} &=&\frac {\left( R_{1}+5\right) \times 6}{\left( R_{1}+5\right) +6} \\[ 5pt ] &=&\frac {\left( 7+5\right) \times 6}{\left( 7+5\right) +6} \\[ 5pt ] &=&4 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となる。さらに$ \ 3 \ \mathrm {\Omega } \ $が直列に接続されているので，端子対$ \ \mathrm {a – b} \ $から二次側を見たときのインピーダンス$ \ Z_{1} \ $は，
\[
\begin{eqnarray}
Z_{1} &=&R_{\mathrm {m}}+3 \\[ 5pt ] &=&4+3 \\[ 5pt ] &=&7 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ロ
$ \ V_{\mathrm {m}} \ $は$ \ V_{\mathrm {0}} \ $のうち$ \ R_{\mathrm {m}} \ \mathrm {[\Omega ]} \ $に加わる電圧の大きさであるから，ワンポイント解説「2.分圧・分流の法則」の通り，
\[
\begin{eqnarray}
V_{\mathrm {m}}&=&\frac {R_{\mathrm {m}}}{3+R_{\mathrm {m}}}V_{\mathrm {0}} \\[ 5pt ] &=&\frac {4}{3+4}V_{\mathrm {0}} \\[ 5pt ] &=&\frac {4}{7}V_{\mathrm {0}} \\[ 5pt ] \frac {V_{\mathrm {m}}}{V_{\mathrm {0}}}&=&\frac {4}{7} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：イ
$ \ V_{\mathrm {1}} \ $は$ \ V_{\mathrm {m}} \ $のうち$ \ R_{\mathrm {1}}=7 \ \mathrm {[\Omega ]} \ $に加わる電圧の大きさであるから，ワンポイント解説「2.分圧・分流の法則」の通り，
\[
\begin{eqnarray}
V_{\mathrm {1}}&=&\frac {R_{\mathrm {1}}}{5+R_{\mathrm {1}}}V_{\mathrm {m}} \\[ 5pt ] &=&\frac {7}{5+7}V_{\mathrm {m}} \\[ 5pt ] &=&\frac {7}{12}V_{\mathrm {m}} \\[ 5pt ] \frac {V_{\mathrm {1}}}{V_{\mathrm {m}}}&=&\frac {7}{12} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ニ
（２）及び（３）より，
\[
\begin{eqnarray}
\frac {V_{\mathrm {1}}}{V_{\mathrm {0}}}&=&\frac {V_{\mathrm {1}}}{V_{\mathrm {m}}}\cdot \frac {V_{\mathrm {m}}}{V_{\mathrm {0}}} \\[ 5pt ] &=&\frac {7}{12}\times \frac {4}{7} \\[ 5pt ] &=&\frac {1}{3}\\[ 5pt ] \end{eqnarray}
\] となるので，
\[
\begin{eqnarray}
\frac {V_{\mathrm {2}}}{V_{\mathrm {0}}}&=&\frac {V_{\mathrm {2}}}{V_{\mathrm {1}}}\cdot \frac {V_{\mathrm {1}}}{V_{\mathrm {0}}} \\[ 5pt ] &=&\frac {1}{3}\times \frac {1}{3} \\[ 5pt ] &=&\frac {1}{3^{2}}\\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ト
（４）解答式より，$ \ \displaystyle V_{\mathrm {2}}=\frac {V_{\mathrm {0}}}{9} \ $なので，$ \ R_{1}=7 \ \mathrm {[\Omega ]} \ $で消費する電力$ \ P \ \mathrm {[W]} \ $は，ワンポイント解説「3.抵抗での消費電力」の通り，
\[
\begin{eqnarray}
P&=&\frac {V_{\mathrm {2}}^{2}}{R_{\mathrm {1}}} \\[ 5pt ] &=&\frac {\displaystyle \left( \frac {V_{\mathrm {0}}}{9}\right) ^{2}}{7} \\[ 5pt ] &=&\frac {V_ {0}^{2}}{567}\\[ 5pt ] \end{eqnarray}
\] と求められる。