《理論》〈電磁気〉[R06:問1]誘電率の異なる２つの誘電体を挿入した平行平板コンデンサに関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，誘電体が挿入された平行平板コンデンサに関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

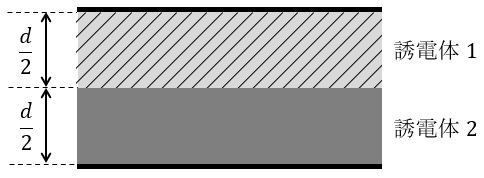
平行平板コンデンサ内を次の$ \ 2 \ $種類の誘電体で完全に満たす。

　誘電体$ \ 1 \ $：誘電率は$ \ \varepsilon _{1} \ $，印加できる最大電界は$ \ E _{\mathrm {1m}} \ $

　誘電体$ \ 2 \ $：誘電率は$ \ \varepsilon _{2} \ $，印加できる最大電界は$ \ E _{\mathrm {2m}} \ $

ただし，$ \ \varepsilon _{1}E _{\mathrm {1m}}＞ \varepsilon _{2}E _{\mathrm {2m}} \ $であり，端効果は無視できるものとする。

図のように誘電体$ \ 1 \ $と$ \ 2 \ $は同体積で，界面が電極と平行になっている。電極間の距離は$ \ d \ $である。このコンデンサにおいて，二つの誘電体内部の$ \ \fbox {　（１）　} \ $の大きさは同じであるので，誘電体$ \ 1 \ $と$ \ 2 \ $の電界をそれぞれ$ \ E _{\mathrm {1}} \ $，$ \ E _{\mathrm {2}} \ $とするとき，$ \ \fbox {　（２）　} \ $の関係が成り立つ。

$ \ \varepsilon _{1}E _{\mathrm {1m}}＞\varepsilon _{2}E _{\mathrm {2m}} \ $なので，印加電圧を上げていくと先に最大電界に達するのは$ \ \fbox {　（３）　} \ $であり，このことから，そのときの電界$ \ E _{\mathrm {1}} \ $，$ \ E _{\mathrm {2}} \ $はそれぞれ$ \ \fbox {　（４）　} \ $である。

したがって，電極間に印加できる最大電圧$ \ V_{\mathrm {m}} \ $は$ \ \fbox {　（５）　} \ $である。

〔問1の解答群〕
\[
\begin{eqnarray}
&（イ）&　誘電体 \ 1　　　　&（ロ）&　\frac {d}{2}\frac {\varepsilon _{1}E _{\mathrm {1m}}+\varepsilon _{2}E _{\mathrm {2m}}}{\varepsilon _{1}+\varepsilon _{2}} \\[ 5pt ] &（ハ）&　誘電体 \ 2　　　　&（ニ）&　\frac {d}{2}\left( 1+\frac {\varepsilon _{2}}{\varepsilon _{1}}\right) E _{\mathrm {2m}} \\[ 5pt ] &（ホ）&　電束密度　　　　&（ヘ）&　\frac {d}{2}\left( 1+\frac {\varepsilon _{1}}{\varepsilon _{2}}\right) E _{\mathrm {1m}} \\[ 5pt ] &（ト）&　電界　　　　&（チ）&　\varepsilon _{1}E _{\mathrm {1}}= \varepsilon _{2}E _{\mathrm {2}} \\[ 5pt ] &（リ）&　分極　　　　&（ヌ）&　\varepsilon _{1}E _{\mathrm {2}}= \varepsilon _{2}E _{\mathrm {1}} \\[ 5pt ] &（ル）&　\left( 1+\frac {\varepsilon _{1}}{\varepsilon _{2}}\right) E _{\mathrm {2}}=\left( 1+\frac {\varepsilon _{2}}{\varepsilon _{1}}\right) E _{\mathrm {1}}　　　　&（ヲ）&　E_{1}=E_{2} \\[ 5pt ] &（ワ）&　E _{\mathrm {1}}=E _{\mathrm {1m}}, E _{\mathrm {2}}=\frac {\varepsilon _{1}}{\varepsilon _{2}}E _{\mathrm {1m}}　　　　&（カ）&　E _{\mathrm {1}}=\frac {\varepsilon _{2}}{\varepsilon _{1}}E _{\mathrm {2m}}, E _{\mathrm {2}}=E _{\mathrm {2m}} \\[ 5pt ] &（ヨ）&　E _{\mathrm {1}}=\frac {\varepsilon _{1}}{\varepsilon _{1}+\varepsilon _{2}}E _{\mathrm {1m}}, E _{\mathrm {2}}=\frac {\varepsilon _{2}}{\varepsilon _{1}+\varepsilon _{2}}E _{\mathrm {2m}} && \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

平行平板コンデンサに関する問題です。
本問の内容は$ \ 3 \ $種の頃から学習してきた定番の内容であるため，例年の電磁気の問題に比べると多くの受験生が高得点を取得できた問題であるかと思います。本問が解けたら令和3年問1に本問よりやや難易度が高めの類題が出題されているので，そちらにも挑戦してみて下さい。

1.ガウスの定理
$ \ Q \ \mathrm {[C]} \ $から出る電気力線は$ \ \displaystyle \frac {Q}{\varepsilon } \ $本，電束は$ \ Q \ $本であり，電界$ \ E \ \mathrm {[V / m]} \ $及び電束密度$ \ D \ \mathrm {[C / m^{2}]} \ $との関係は，任意の閉曲面において，
\[
\begin{eqnarray}
\int _{S} \boldsymbol E \cdot \mathrm {d}\boldsymbol S &=& \frac {Q}{\varepsilon } \\[ 5pt ] \int _{S} \boldsymbol D \cdot \mathrm {d}\boldsymbol S &=& Q \\[ 5pt ] \end{eqnarray}
\] となり，これをガウスの定理といいます。

2.平行平板コンデンサの電界$ \ E \ $と電圧$ \ V \ $の関係
極板間の距離$ \ d \ \mathrm {[m]} \ $の平行平板コンデンサに電圧$ \ V \ \mathrm {[V]} \ $を加えると，極板間の電界$ \ E \ \mathrm {[V / m]} \ $は，
\[
\begin{eqnarray}
E&=&\frac {V}{d} \\[ 5pt ] \end{eqnarray}
\] となります。

3.平行平板コンデンサの電束密度$ \ D \ $と電界$ \ E \ $の関係
極板間の誘電率を$ \ \varepsilon \ \mathrm {[F / m]} \ $とすると，電束密度$ \ D \ \mathrm {[C / m^{2}]} \ $と電界$ \ E \ \mathrm {[V / m]} \ $には，
\[
\begin{eqnarray}
D&=&\varepsilon E \\[ 5pt ] \end{eqnarray}
\] の関係があります。真空の誘電率を$ \ \varepsilon _{0} \ \mathrm {[F / m]} \ $，誘電体の比誘電率を$ \ \varepsilon _{\mathrm {r}} \ $とすると，$ \ \varepsilon = \varepsilon _{\mathrm {r}}\varepsilon _{0} \ $の関係があるので，
\[
\begin{eqnarray}
D&=&\varepsilon _{\mathrm {r}}\varepsilon _{0}E \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)解答：ホ
ワンポイント解説「1.ガウスの定理」の通り，蓄えられている電荷が同じであれば，誘電体の誘電率に関係なく電束密度の大きさは等しくなる。

(2)解答：チ
誘電体$ \ 1 \ $と$ \ 2 \ $の電界をそれぞれ$ \ E _{\mathrm {1}} \ $，$ \ E _{\mathrm {2}} \ $としたときの各誘電体における電束密度$ \ D \ $は等しいので，ワンポイント解説「3.平行平板コンデンサの電束密度$ \ D \ $と電界$ \ E \ $の関係」の通り，
\[
\begin{eqnarray}
D&=&\varepsilon _{\mathrm {1}}E_{\mathrm {1}}=\varepsilon _{\mathrm {2}}E_{\mathrm {2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ハ
(2)解答式及び$ \ \varepsilon _{1}E _{\mathrm {1m}}＞\varepsilon _{2}E _{\mathrm {2m}} \ $より，誘電体$ \ 2 \ $の電界が$ \ E _{\mathrm {2m}} \ $に到達しても，誘電体$ \ 1 $は最大電界に到達しないので，先に最大電界に達するのは誘電体$ \ 2 \ $と求められる。

(4)解答：カ
(2)解答式及び(3)解答より，$ \ E_{\mathrm {2}}=E _{\mathrm {2m}} \ $のときの電界$ \ E _{\mathrm {1}} \ $は，
\[
\begin{eqnarray}
\varepsilon _{\mathrm {1}}E_{\mathrm {1}}&=&\varepsilon _{\mathrm {2}}E_{\mathrm {2m}} \\[ 5pt ] E_{\mathrm {1}}&=&\frac {\varepsilon _{\mathrm {2}}}{\varepsilon _{\mathrm {1}}}E_{\mathrm {2m}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ニ
(4)解答式より，電極間に印加できる最大電圧$ \ V_{\mathrm {m}} \ $は，ワンポイント解説「2.平行平板コンデンサの電界$ \ E \ $と電圧$ \ V \ $の関係」の通り，
\[
\begin{eqnarray}
V_{\mathrm {m}}&=&E_{\mathrm {1}}\cdot \frac {d}{2}+E_{\mathrm {2}}\cdot \frac {d}{2} \\[ 5pt ] &=&\frac {\varepsilon _{\mathrm {2}}}{\varepsilon _{\mathrm {1}}}E_{\mathrm {2m}}\cdot \frac {d}{2}+E _{\mathrm {2m}}\cdot \frac {d}{2} \\[ 5pt ] &=&\frac {d}{2}\left( 1+\frac {\varepsilon _{2}}{\varepsilon _{1}}\right) E _{\mathrm {2m}}
\end{eqnarray}
\] と求められる。