Contents
【問題】
【難易度】★★★★☆(やや難しい)
図は単相\( \ 2 \ \)線式の配電線路の単線図である。 電線\( \ 1 \ \)線当たりの抵抗と長さは,\( \ \mathrm {a-b} \ \)間で\( \ 0.3 \ \mathrm {[\Omega / km]} \ \),\( \ 250 \ \mathrm {[m]} \ \),\( \ \mathrm {b-c} \ \)間で\( \ 0.9 \ \mathrm {[\Omega / km]} \ \),\( \ 100 \ \mathrm {[m]} \ \)とする。次の(a)及び(b)に答えよ。
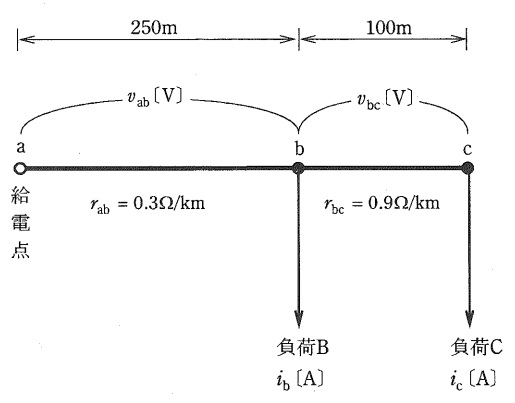
(a) \( \ \mathrm {b-c} \ \)間の\( \ 1 \ \)線の電圧降下\( \ v_{\mathrm {bc}} \ \mathrm {[V]} \ \)及び負荷\( \ \mathrm {B} \ \)と負荷\( \ \mathrm {C} \ \)の負荷電流\( \ i_{\mathrm {b}} \ \),\( \ i_{\mathrm {c}} \ \mathrm {[A]} \ \)として,正しいものを組み合わせたのは次のうちどれか。
ただし,給電点\( \ \mathrm {a} \ \)の線間の電圧値と負荷点\( \ \mathrm {c} \ \)の線間の電圧値の差を\( \ 12.0 \ \mathrm {[V]} \ \)とし,\( \ \mathrm {a-b} \ \)間の\( \ 1 \ \)線の電圧降下\( \ v_{\mathrm {ab}}=3.75 \ \mathrm {[V]} \ \)とする。 負荷の力率はいずれも\( \ 100 \ \mathrm {[%]} \ \),線路リアクタンスは無視するものとする。
\[
\begin{array}{cccccc}
& v_{\mathrm {bc}} \ \mathrm {[V]} & i_{\mathrm {b}} \ \mathrm {[A]} & i_{\mathrm {c}} \ \mathrm {[A]} \\
\hline
(1) & 2.25 & 10.0 & 40.0 \\
\hline
(2) & 2.25 & 25.0 & 25.0 \\
\hline
(3) & 4.50 & 10.0 & 25.0 \\
\hline
(4) & 4.50 & 0.0 & 50.0 \\
\hline
(5) & 8.25 & 50.0 & 91.7 \\
\hline
\end{array}
\]
(b) 次に,図の配電線路で抵抗に加えて\( \ \mathrm {a-c} \ \)間の往復線路のリアクタンスを考慮する。このリアクタンスを\( \ 0.1 \ \mathrm {[\Omega ]} \ \)とし,\( \ \mathrm {b} \ \)点には無負荷で\( \ i_{\mathrm {b}}=0 \ \mathrm {[A]} \ \),\( \ \mathrm {c} \ \)点には受電電圧が\( \ 100 \ \mathrm {[V]} \ \),遅れ力率\( \ 0.8 \ \),\( \ 1.5 \ \mathrm {[kW]} \ \)の負荷が接続されているものとする。
このとき,給電点\( \ \mathrm {a} \ \)の線間の電圧値と負荷点\( \ \mathrm {c} \ \)の線間の電圧値\( \ \mathrm {[V]} \ \)の差として,最も近いのは次のうちどれか。
(1) \( \ 3.0 \ \) (2) \( \ 4.9 \ \) (3) \( \ 5.3 \ \) (4) \( \ 6.1 \ \) (5) \( \ 37.1 \ \)
【ワンポイント解説】
配電線の電圧降下と線路電流に関する問題です。
単相\( \ 2 \ \)線式の問題は電圧降下を検討する際に往復の電圧降下を考慮する必要がありますが,それを忘れてしまう受験生が非常に多いです。
ミスを防止するために,まずは図を描いて回路図から導出用法を検討すると良いかと思います。
1.配電線の電圧降下の近似式
①単相\( \ 2 \ \)線式送電線の電圧降下
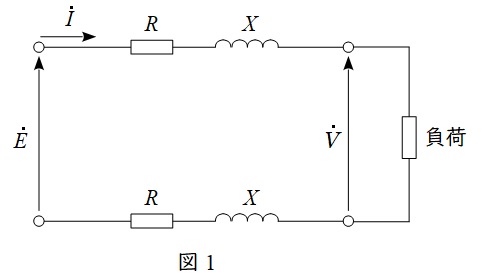
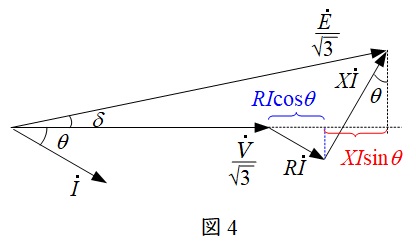
単相\( \ 2 \ \)線式線路は図1のような回路になり,負荷に対して供給される線路と戻りの線路の\( \ 2 \ \)段階で電圧降下が発生します。したがって,負荷の力率が遅れ力率\( \ \cos \theta \ \)であるときのベクトル図を描くと図2のようになります。
図2のベクトル図において,\( \ \dot E \ \)と\( \ \dot V \ \)の位相差が十分に小さいと仮定すると,線路の電圧降下\( \ \varepsilon =E-V \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
E&≃&V+2RI\cos \theta +2XI\sin \theta \\[ 5pt ]
E-V&=&2RI\cos \theta +2XI\sin \theta \\[ 5pt ]
\varepsilon &=&2I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
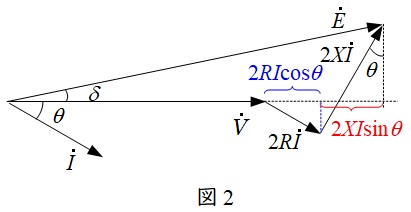
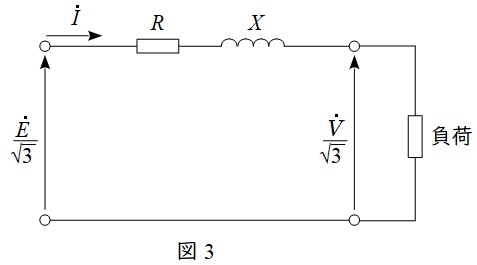
②三相\( \ 3 \ \)線式送電線の電圧降下
三相回路においては,一相分の等価回路及びベクトル図は図3及び図4のように描くことができ,三相分の電圧降下\( \ \varepsilon \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
\frac {E}{\sqrt {3}}&≃&\frac {V}{\sqrt {3}}+RI\cos \theta +XI\sin \theta \\[ 5pt ]
\frac {E}{\sqrt {3}}-\frac {V}{\sqrt {3}}&=&RI\cos \theta +XI\sin \theta \\[ 5pt ]
E-V&=&\sqrt {3}\left( RI\cos \theta +XI\sin \theta \right) \\[ 5pt ]
\varepsilon &=&\sqrt {3}I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
2.線路の有効電力\( \ P \ \)
①単相\( \ 2 \ \)線式
単相\( \ 2 \ \)線式の配電線の線間電圧が\( \ V \ \mathrm {[V]} \ \),線電流が\( \ I \ \mathrm {[A]} \ \),電圧と電流の力率が\( \ \cos \theta \ \)であるとき,送電電力\( \ P \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P &=&VI\cos \theta \\[ 5pt ]
\end{eqnarray}
\]
となります。
②三相\( \ 3 \ \)線式
三相\( \ 3 \ \)線式の配電線の線間電圧が\( \ V \ \mathrm {[V]} \ \),線電流が\( \ I \ \mathrm {[A]} \ \),電圧と電流の力率が\( \ \cos \theta \ \)であるとき,送電電力\( \ P \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P &=&\sqrt {3}VI\cos \theta \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(a)解答:(2)
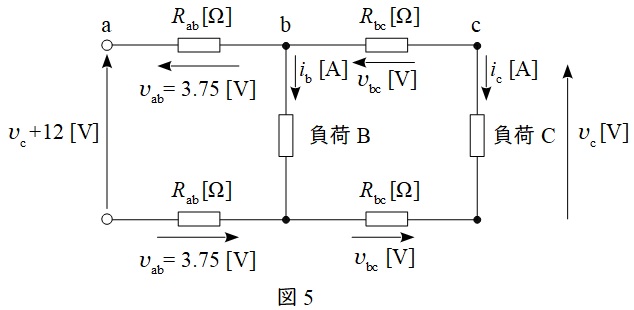
題意に沿って回路図を描くと図5のようになる。
図5についてキルヒホッフの法則を適用すると,
\[
\begin{eqnarray}
v_{\mathrm {c}}+12 &=&v_{\mathrm {ab}}+v_{\mathrm {bc}}+v_{\mathrm {c}}+v_{\mathrm {bc}}+v_{\mathrm {ab}} \\[ 5pt ]
&=&2v_{\mathrm {ab}}+2v_{\mathrm {bc}}+v_{\mathrm {c}} \\[ 5pt ]
12&=&2v_{\mathrm {ab}}+2v_{\mathrm {bc}} \\[ 5pt ]
6&=&v_{\mathrm {ab}}+v_{\mathrm {bc}} \\[ 5pt ]
v_{\mathrm {bc}}&=&6-v_{\mathrm {ab}} \\[ 5pt ]
&=&6-3.75 \\[ 5pt ]
&=&2.25 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。\( \ \mathrm {a-b} \ \)間の抵抗\( \ R_{\mathrm {ab}} \ \mathrm {[\Omega ]} \ \)及び\( \ \mathrm {b-c} \ \)間の抵抗\( \ R_{\mathrm {bc}} \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
R_{\mathrm {ab}} &=&r_{\mathrm {ab}}\times 0.25 \\[ 5pt ]
&=&0.3\times 0.25 \\[ 5pt ]
&=&0.075 \ \mathrm {[\Omega ]} \\[ 5pt ]
R_{\mathrm {bc}} &=&r_{\mathrm {bc}}\times 0.1 \\[ 5pt ]
&=&0.9\times 0.1 \\[ 5pt ]
&=&0.09 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,負荷\( \ \mathrm {C} \ \)に流れる電流\( \ i_{\mathrm {c}} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
i_{\mathrm {c}} &=&\frac {v_{\mathrm {bc}}}{R_{\mathrm {bc}}} \\[ 5pt ]
&=&\frac {2.25}{0.09} \\[ 5pt ]
&=&25 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,\( \ \mathrm {a-b} \ \)間を流れる電流が\( \ i_{\mathrm {b}}+i_{\mathrm {c}} \ \mathrm {[A]} \ \)であるから,
\[
\begin{eqnarray}
i_{\mathrm {b}}+i_{\mathrm {c}} &=&\frac {v_{\mathrm {ab}}}{R_{\mathrm {ab}}} \\[ 5pt ]
i_{\mathrm {b}} &=&\frac {v_{\mathrm {ab}}}{R_{\mathrm {ab}}}-i_{\mathrm {c}} \\[ 5pt ]
&=&\frac {3.75}{0.075}-25 \\[ 5pt ]
&=&25 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
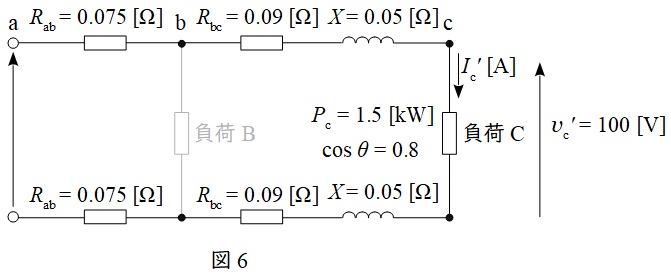
(b)解答:(4)
往復線路のリアクタンスが\( \ 0.1 \ \mathrm {[\Omega ]} \ \)であるから,\( \ 1 \ \)線あたりのリアクタンスは\( \ X=0.05 \ \mathrm {[\Omega ]} \ \)となり,回路図は図6のように描ける。
負荷\( \ \mathrm {C} \ \)に流れる電流\( \ i_{\mathrm {c}}^{\prime } \ \mathrm {[A]} \ \)は,ワンポイント解説「2.線路の有効電力\( \ P \ \)」の通り,
\[
\begin{eqnarray}
P_{\mathrm {c}} &=&v_{\mathrm {c}}^{\prime }i_{\mathrm {c}}^{\prime }\cos \theta \\[ 5pt ]
i_{\mathrm {c}}^{\prime } &=&\frac {P_{\mathrm {c}}}{v_{\mathrm {c}}^{\prime }\cos \theta } \\[ 5pt ]
&=&\frac {1.5\times 10^{3}}{100\times 0.8} \\[ 5pt ]
&=&18.75 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \sin \theta \ \)は,
\[
\begin{eqnarray}
\sin \theta &=&\sqrt {1-\cos ^{2}\theta } \\[ 5pt ]
&=&\sqrt {1-0.8 ^{2}} \\[ 5pt ]
&=&0.6 \\[ 5pt ]
\end{eqnarray}
\]
であるから,\( \ \mathrm {a} \ \)点と\( \ \mathrm {c} \ \)点の電圧値の差,すなわち電圧降下\( \ \varepsilon \ \mathrm {[V]} \ \)は,ワンポイント解説「1.配電線の電圧降下の近似式」より,
\[
\begin{eqnarray}
\varepsilon &=&2i_{\mathrm {c}}^{\prime }\left( R_{\mathrm {ac}}\cos \theta +X\sin \theta \right) \\[ 5pt ]
&=&2i_{\mathrm {c}}^{\prime }\left\{ \left( R_{\mathrm {ab}}+R_{\mathrm {bc}}\right) \cos \theta +X\sin \theta \right\} \\[ 5pt ]
&=&2\times 18.75\times \left\{ \left( 0.075+0.09\right) \times 0.8 +0.05\times 0.6 \right\} \\[ 5pt ]
&≒&6.1 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは