《電力》〈火力〉[H25:問15]火力発電所の効率計算に関する計算問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★★（難しい）

復水器の冷却に海水を使用する汽力発電所が定格出力で運転している。次の(a)及び(b)の問に答えよ。

(a)　この発電所の定格出力運転時には発電端熱効率が\( \ 38 \ \mathrm {[％]} \ \)，燃料消費量が\( \ 40 \ \mathrm {[t／h]} \ \)である。\( \ 1 \ \)時間当たりの発生電力量\( \ \mathrm {[MW\cdot h]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし，燃料発熱量は\( \ 44000 \ \mathrm {[kJ／kg]} \ \)とする。

　(1)　\( \ 186 \ \)　　(2)　\( \ 489 \ \)　　(3)　\( \ 778 \ \)　　(4)　\( \ 1286 \ \)　　(5)　\( \ 2046 \ \)

(b)　定格出力で運転を行ったとき，復水器冷却水の温度上昇を\( \ 7 \ \mathrm {[K]} \ \)とするために必要な復水器冷却水の流量\( \ \mathrm {[m^{3}／s]} \ \)の値として，最も近いものを次の(1)～(5)のうちから一つ選べ。

ただし，タービン熱消費率を\( \ 8000 \ \mathrm {[kJ／\left( kW\cdot h\right) ]} \ \)，海水の比熱と密度をそれぞれ\( \ 4.0 \ \mathrm {[kJ／\left( kg\cdot K\right) ]} \ \)，\( \ 1.0\times 10^{3} \ \mathrm {[kg／m^{3}]} \ \)，発電機効率を\( \ 98 \ \mathrm {[％]} \ \)とし，提示されていない条件は無視する。

　(1)　\( \ 6.8 \ \)　　(2)　\( \ 8.0 \ \)　　(3)　\( \ 14.8 \ \)　　(4)　\( \ 17.9 \ \)　　(5)　\( \ 21.0 \ \)

【ワンポイント解説】

(a)は標準～やや難易度高めの問題ですが，(b)は火力発電所の概略フローが頭の中に入っている前提で，計算力を要する難問です。熱消費率や冷却水量の内容もあり，難易度としては二種や一種の二次試験に出題されても良いような内容と言えると思います。

1.熱量と電力量の関係
\( \ 1 \ \mathrm {[kW\cdot h]} \ \)は\( \ 1 \ \mathrm {[kW]} \ \)の電力で\( \ 1 \ \)時間運転した時の電力量です。
また，\( \ 1 \ \mathrm {[W\cdot s]}=1 \ \mathrm {[J]} \ \)の関係があります。したがって，
\[
\begin{eqnarray}
1 \ \mathrm {[kW\cdot h]}&=&3600 \ \mathrm {[kW\cdot s]} \\[ 5pt ] &=&3600 \ \mathrm {[kJ]} \\[ 5pt ] \end{eqnarray}
\] の関係があります。また，上式から電力と\( \ 1 \ \)時間当たりの熱量の関係は，
\[
\begin{eqnarray}
1 \ \mathrm {[kW]}&=&3600 \ \mathrm {[kJ／h]} \\[ 5pt ] \end{eqnarray}
\] となります。

2.発電端熱効率\( \ \eta \ \)
燃料の熱量に対してどの程度発電したかを示す指標です。
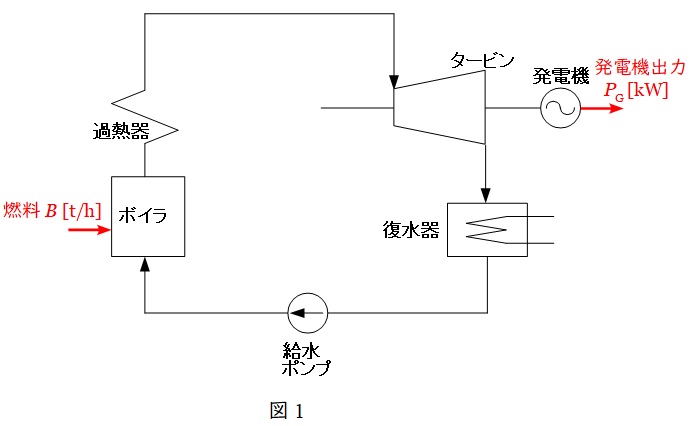
図1において，燃料消費量を\( \ B \ \mathrm {[t／h]} \ \)，発電機出力を\( \ P_{\mathrm {G}} \ \mathrm {[kW]} \ \)であったとし，燃料発熱量を\( \ H \ \mathrm {[kJ／kg]} \ \)とすると，単位時間あたりの燃料消費量は，
\[
\begin{eqnarray}
B \ \mathrm {[t／h]} &=&1000B \ \mathrm {[kg／h]} \\[ 5pt ] &=&\frac {1000}{3600}B \ \mathrm {[kg／s]} \\[ 5pt ] \end{eqnarray}
\] であるから，発電端熱効率\( \ \eta \ \)は，
\[
\begin{eqnarray}
\eta &=&\frac {P_{\mathrm {G}}}{\displaystyle \frac {1000}{3600}B\times H} \times 100 \\[ 5pt ] &=&\frac {3.6P_{\mathrm {G}}}{BH} \times 100 \ \mathrm {[％]} \\[ 5pt ] \end{eqnarray}
\] となります。

3.熱消費率\( \ q \ \)
電力量\( \ 1 \ \mathrm {[kW\cdot h]} \ \)を発電するのに必要な熱量\( \ \mathrm {[kJ]} \ \)を示す指標で，火力発電所での効率管理に使用されます。実質的には電力\( \ 1 \ \mathrm {[kW]} \ \)に対する\( \ 1 \ \)時間あたりの熱量\( \ \mathrm {[kJ／h]} \ \)が使用されます。
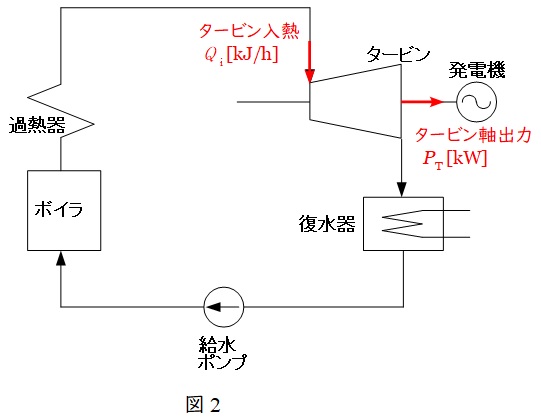
図2においてタービン熱消費率を\( \ q_{\mathrm {t}} \ \)とすると，
\[
\begin{eqnarray}
q_{\mathrm {t}} &=&\frac {Q_{\mathrm {i}}}{P_{\mathrm {T}}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(a)解答：(1)
ワンポイント解説「2.発電端熱効率\( \ \eta \ \)」より，各値を代入すると，
\[
\begin{eqnarray}
P_{\mathrm {G}}&=&\frac {BH\eta }{3.6 \times 100} \\[ 5pt ] &=&\frac {40\times 44000\times 38 }{3.6 \times 100} \\[ 5pt ] &≒&185800 \ \mathrm {[kW]}　→　186 \ \mathrm {[MW]} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ 1 \ \mathrm {[kW\cdot h]} \ \)は\( \ 1 \ \mathrm {[kW]} \ \)の電力で\( \ 1 \ \)時間運転した時の電力量であるから，\( \ 186 \ \mathrm {[MW]} \ \)の電力で\( \ 1 \ \)時間運転した時の電力量は，\( \ 186 \ \mathrm {[MW\cdot h]} \ \)となる。

(b)解答：(2)
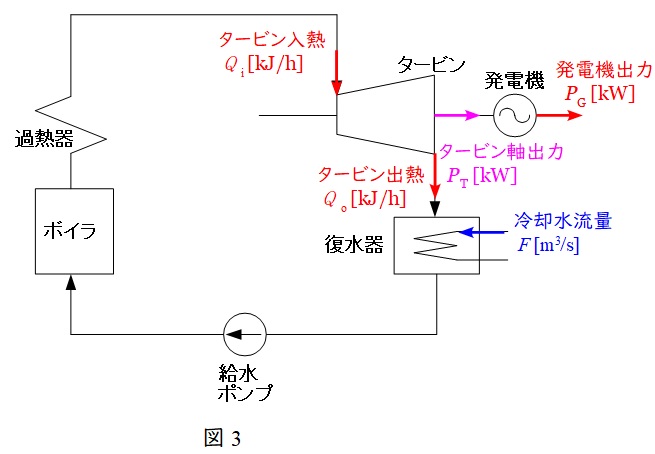
各値を図3の通りとする。発電機効率が\( \ 98 \ \mathrm {[％]} \ \)であるから，タービン軸出力\( \ P_{\mathrm {T}} \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {T}}&=&\frac {P_{\mathrm {G}}}{0.98} \\[ 5pt ] &=&\frac {185800}{0.98} \\[ 5pt ] &≒&189600 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] となる。ワンポイント解説「3.熱消費率\( \ q \ \)」より，タービンの入熱\( \ Q_{\mathrm {i}} \ \)は，
\[
\begin{eqnarray}
Q_{\mathrm {i}}&=&q_{\mathrm {t}}P_{\mathrm {T}} \\[ 5pt ] &=&8000 \times 189600 \\[ 5pt ] &≒&1517000000 \ \mathrm {[kJ／h]} \\[ 5pt ] \end{eqnarray}
\] となる。\( \ 1 \ \mathrm {[kW]}=3600 \ \mathrm {[kJ／h]} \ \)であるからタービンの出熱\( \ Q_{\mathrm {o}} \ \)は，
\[
\begin{eqnarray}
Q_{\mathrm {o}}&=&Q_{\mathrm {i}}-3600P_{\mathrm {T}} \\[ 5pt ] &=&1517000000-3600\times 189600 \\[ 5pt ] &≒&834400000\ \mathrm {[kJ／h]} \\[ 5pt ] \end{eqnarray}
\] となる。タービンの出熱\( \ Q_{\mathrm {o}} \ \)と復水器での熱交換量が等しいので，
\[
\begin{eqnarray}
Q_{\mathrm {o}}&=&4.0\times 1.0\times 10^{3}\times F\times 3600 \times 7 \\[ 5pt ] F&=&\frac {Q_{\mathrm {o}}}{4.0\times 1.0\times 10^{3}\times 3600 \times 7 } \\[ 5pt ] &=&\frac {834400000}{4.0\times 1.0\times 10^{3}\times 3600 \times 7 } \\[ 5pt ] &≒&8.28　→　8.0 \ \mathrm {[m^{3}／s]} \\[ 5pt ] \end{eqnarray}
\] と求められる。