《電力》〈配電〉[H25:問9]架線の張力と支線と追支線の関係に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

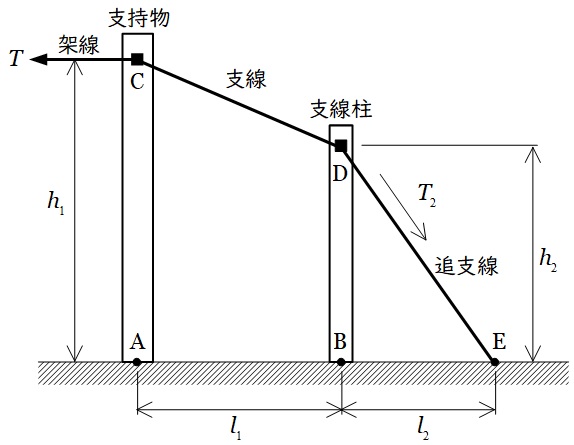
図のように，架線の水平張力\( \ T \ \mathrm {[N]} \ \)を支線と追支線で，支持物と支線柱を介して受けている。支持物の固定点\( \ \mathrm {C} \ \)の高さを\( \ h_{1} \ \mathrm {[m]} \ \)，支線柱の固定点\( \ \mathrm {D} \ \)の高さを\( \ h_{2} \ \mathrm {[m]} \ \)とする。また，支持物と支線柱間の距離\( \ \mathrm {AB} \ \)を\( \ l_{1} \ \mathrm {[m]} \ \)，支線柱と追支線地上固定点\( \ \mathrm {E} \ \)との根開き\( \ \mathrm {BE} \ \)を\( \ l_{2} \ \mathrm {[m]} \ \)とする。

支持物及び支線柱が受ける水平方向の力は，それぞれ平衡しているという条件で，追支線にかかる張力\( \ T_{2} \ \mathrm {[N]} \ \)を表した式として，正しいものを次の(1)～(5)のうちから一つ選べ。

ただし，支線，追支線の自重及び提示していない条件は無視する。

\[
\begin{eqnarray}
& \left( 1\right) & \frac {T\sqrt {{h_{2}}^{2}+{l_{2}}^{2}}}{l_{2}}　　& \left( 2\right) & \frac {Tl_{2}}{\sqrt {{h_{2}}^{2}+{l_{2}}^{2}}}　　& \left( 3\right) & \frac {T\sqrt {{h_{2}}^{2}+{l_{2}}^{2}}}{\sqrt {\left( h_{1}-h_{2}\right) ^{2}+{l_{1}}^{2}}} \\[ 5pt ] & \left( 4\right) & \frac {T\sqrt {\left( h_{1}-h_{2}\right) ^{2}+{l_{1}}^{2}}}{\sqrt {{h_{2}}^{2}+{l_{2}}^{2}}}　　& \left( 5\right) & \frac {Th_{2}\sqrt {\left( h_{1}-h_{2}\right) ^{2}+{l_{1}}^{2}}}{\left( h_{1}-h_{2}\right) \sqrt {{h_{2}}^{2}+{l_{2}}^{2}}}　　& & \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

電線の張力に関する問題です。水平張力が釣り合っているという条件が入っているのでそれに沿って求めることが重要となります。

【解答】

解答：(1)
支線及び追支線にかかる張力をそれぞれ\( \ T_{1} \ \)及び\( \ T_{2} \ \)，支線及び追支線と水平とのなす角を\( \ \theta _{1} \ \)及び\( \ \theta _{2} \ \)とする。各部の張力及び角度は図1の通りとなる。
題意より，支持物及び支線柱が受ける水平方向の力は平衡しているので，
\[
\begin{eqnarray}
T &=& T_{1}\cos \theta _{1}　&・・・・・・・・・・①& \\[ 5pt ] T_{1}\cos \theta _{1} &=& T_{2}\cos \theta _{2}　&・・・・・・・・・・②& \\[ 5pt ] \end{eqnarray}
\] となる。①，②より，\( \ T_{1}\cos \theta _{1} \ \)を消去すると，
\[
\begin{eqnarray}
T &=& T_{2}\cos \theta _{2}　　　　　　　&・・・・・・・・・・③& \\[ 5pt ] \end{eqnarray}
\] となる。ここで，\( \ \cos \theta _{2} \ \)は追支線の長さが\( \ \sqrt {{h_{2}}^{2}+{l_{2}}^{2}} \ \)であるから，
\[
\begin{eqnarray}
\cos \theta _{2} &=&\frac {l_{2}}{\sqrt {{h_{2}}^{2}+{l_{2}}^{2}}} \\[ 5pt ] \end{eqnarray}
\] となるので，これを③に代入して整理すると，
\[
\begin{eqnarray}
T &=& T_{2}\times \frac {l_{2}}{\sqrt {{h_{2}}^{2}+{l_{2}}^{2}}} \\[ 5pt ] T_{2} &=& \frac {T\sqrt {{h_{2}}^{2}+{l_{2}}^{2}}}{l_{2}} \\[ 5pt ] \end{eqnarray}
\] と求められる。