《電力》〈水力〉[H28:問1]揚水発電所の出力や入力及び効率に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

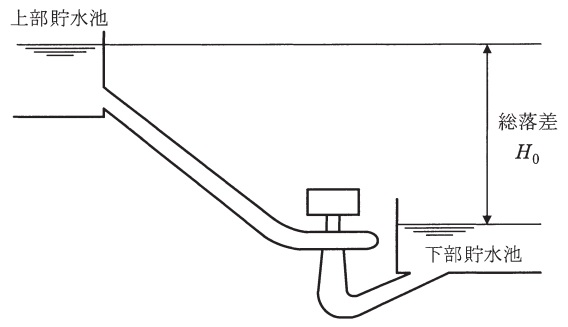
下記の諸元の揚水発電所を，運転中の総落差が変わらず，発電出力，揚水入力ともに一定で運転するものと仮定する。この揚水発電所における発電出力の値\( \ \mathrm {[ kW ] } \ \)，揚水入力の値\( \ \mathrm {[ kW ] } \ \)，揚水所要時間の値\( \ \mathrm {[ h ] } \ \)及び揚水総合効率の値\( \ \mathrm {[ ％ ] } \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

揚水発電所の諸元
　総落差　　　　　　　　　　\(H_{0}=400 \ \mathrm {m}\)
　発電損失水頭　　　　　　　\(h_{\mathrm {G}}=H_{0}の3 \ ％\)
　揚水損失水頭　　　　　　　\(h_{\mathrm {P}}=H_{0}の3 \ ％\)　
　発電使用水量　　　　　　　\(Q_{\mathrm {G}}=60 \ \mathrm {m^{3} / s }\)
　揚水量　　　　　　　　　　\(Q_{\mathrm {P}}=50 \ \mathrm {m^{3} / s }\)
　発電運転時の効率　　　　　発電機効率\(\eta _{\mathrm {G}}\times\)水車効率\(\eta _{\mathrm {T}} =87 \ ％\)
　ポンプ運転時の効率　　　　電動機効率\(\eta _{\mathrm {M}}\times\)ポンプ効率\(\eta _{\mathrm {P}} =85 \ ％\)
　発電運転時間　　　　　　　\(T_{\mathrm {G}}=8 \ \mathrm {h}\)

\[
\begin{array}{cccccc}
& 発電出力 & 揚水入力 & 揚水所要時間 & 揚水総合効率 \\
& \mathrm {[kW]} & \mathrm {[kW]} & \mathrm {[h]} & \mathrm {[％]} \\
\hline
(1) & 204 \ 600 & 230 \ 600 & 9.6 & 74.0 \\
\hline
(2) & 204 \ 600 & 230 \ 600 & 10.0 & 71.0 \\
\hline
(3) & 198 \ 500 & 237 \ 500 & 9.6 & 71.0 \\
\hline
(4) & 198 \ 500 & 237 \ 500 & 10.0 & 69.6 \\
\hline
(5) & 198 \ 500 & 237 \ 500 & 9.6 & 69.6 \\
\hline
\end{array}
\]

【ワンポイント解説】

発電出力，揚水入力，総合効率の公式はすべて非常に重要な公式です。必ずマスターしておいて下さい。

1.揚水発電所の諸公式
本問に与えられている各値を用いると，各値は下記のように求められます。

①発電電力
有効落差　：\(H=H_{0}-h_{\mathrm {G}} \ \mathrm {[ m ] }\)
発電機出力：\(P_{\mathrm {G}}=9.8Q_{\mathrm {G}}H\eta _{\mathrm {G}}\eta _{\mathrm {T}} \ \mathrm {[ kW ] }\)
総発電量　：\(W_{\mathrm {G}}=P_{\mathrm {G}}T_{\mathrm {G}} \ \mathrm {[ kWh ] }\)

②揚水動力
必要揚程　：\(\displaystyle H_{\mathrm {P}}=H_{0}+h_{\mathrm {P}} \ \mathrm {[ m ] }\)
所要動力　：\(\displaystyle P_{\mathrm {M}}=\frac { 9.8Q_{\mathrm {P}}H_{\mathrm {P}}}{\eta _{\mathrm {M}} \eta _{\mathrm {P}}} \ \mathrm {[ kW ] }\)
所要電力量：\(W_{\mathrm {M}}=P_{\mathrm {M}}T_{\mathrm {M}} \ \mathrm {[ kWh ] }\)

③揚水総合効率
\[
\eta =\frac {W_{\mathrm {G}}}{W_{\mathrm {M}}}\times 100 \ \mathrm {[ ％ ] }
\]

【解答】

解答：(5)
①発電出力
有効落差\( \ H \ \)は，
\[
\begin{eqnarray}
H&=&H_{0}-h_{\mathrm {G}} \\[ 5pt ] &=&400-0.03\times 400 \\[ 5pt ] &=&388 \ \mathrm {[ m ] }
\end{eqnarray}
\] であるから，発電出力\( \ P_{\mathrm {G}} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {G}}&=&9.8Q_{\mathrm {G}}H\eta _{\mathrm {G}}\eta _{\mathrm {T}} \\[ 5pt ] &=&9.8\times 60 \times 388 \times 0.87 \\[ 5pt ] &≒&198485　→　198500 \ \mathrm {[ kW ] }
\end{eqnarray}
\] と求められる。

②揚水入力
必要揚程\( \ H_{\mathrm {P}} \ \)は，
\[
\begin{eqnarray}
H_{\mathrm {P}}&=&H_{0}+h_{\mathrm {P}} \\[ 5pt ] &=&400+0.03\times 400 \\[ 5pt ] &=&412 \ \mathrm {[ m ] }
\end{eqnarray}
\] であるから，揚水入力\( \ P_{\mathrm {M}} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {M}}&=&\frac { 9.8Q_{\mathrm {P}}H_{\mathrm {P}}}{\eta _{\mathrm {M}} \eta _{\mathrm {P}}} \\[ 5pt ] &=&\frac { 9.8\times 50 \times 412}{0.85} \\[ 5pt ] &≒&237506　→　237500 \ \mathrm {[ kW ] }
\end{eqnarray}
\] と求められる。

③揚水所要時間
発電に利用した水量と揚水に使用した水量は等しいので，揚水所要時間を\( \ T_{\mathrm {M}} \ \)とすると，
\[
\begin{eqnarray}
Q_{\mathrm {G}}\times 3600\times T_{\mathrm {G}}&=&Q_{\mathrm {P}}\times 3600\times T_{\mathrm {M}} \\[ 5pt ] 60\times 3600\times 8&=&50\times 3600\times T_{\mathrm {M}} \\[ 5pt ] T_{\mathrm {M}}&=&9.6 \ \mathrm {[ h ] }
\end{eqnarray}
\] と求められる。

④揚水総合効率
揚水総合効率\( \ \eta \ \)は，
\[
\begin{eqnarray}
\eta &=&\frac {W_{\mathrm {G}}}{W_{\mathrm {M}}}\times 100 \\[ 5pt ] &=&\frac {P_{\mathrm {G}}T_{\mathrm {G}}}{P_{\mathrm {M}}T_{\mathrm {M}}}\times 100 \\[ 5pt ] &=&\frac {198485\times 8}{237506\times 9.6}\times 100 \\[ 5pt ] &≒&69.6 \ \mathrm {[ ％ ] }
\end{eqnarray}
\] と求められる。