《電力》〈火力〉[H28:問15]汽力発電所のタービン効率及び発電機効率に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

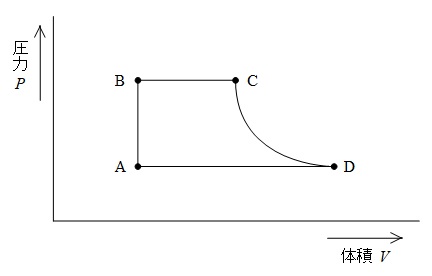
図は，あるランキンサイクルによる汽力発電所の\( \ P-V \ \)線図である。この発電所が，\( \ \mathrm{A} \ \)点の比エンタルピー\( \ \mathrm {140 \ kJ/kg} \ \)，\( \ \mathrm {B} \ \)点の比エンタルピー\( \ \mathrm {150 \ kJ/kg} \ \)，\( \ \mathrm {C} \ \)点の比エンタルピー\( \ \mathrm {3380 \ kJ/kg} \ \)，\( \ \mathrm {D} \ \)点の比エンタルピー\( \ \mathrm {2560 \ kJ/kg} \ \)，蒸気タービンの使用蒸気量\( \ \mathrm {100 \ t/h} \ \)，蒸気タービンの出力\( \ \mathrm {18 \ MW} \ \)で運転しているとき，次の(a)及び(b)の問に答えよ。

(a)　タービン効率の値\( \ \mathrm {[ ％ ]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 58.4 \ \)　　(2)　\( \ 66.8 \ \)　　(3)　\( \ 79.0 \ \)　　(4)　\( \ 95.3 \ \)　　(5)　\( \ 96.7 \ \)

(b)　この発電所の送電端電力\( \ \mathrm {16 \ MW} \ \)，所内比率\( \ \mathrm {5 \ ％} \ \)のとき，発電機効率の値\( \ \mathrm {[ ％ ]} \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

　(1)　\( \ 84.7 \ \)　　(2)　\( \ 88.6 \ \)　　(3)　\( \ 88.9 \ \)　　(4)　\( \ 89.2 \ \)　　(5)　\( \ 93.6 \ \)

【ワンポイント解説】

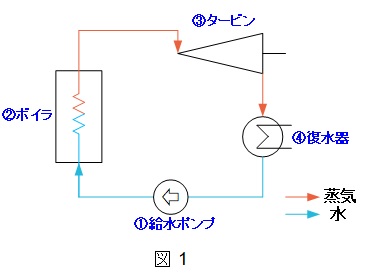
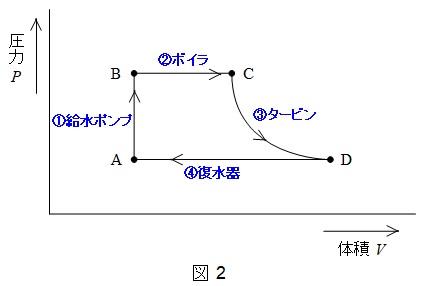
図1に火力発電所のイメージ図（実際にはもっと複雑です。）と図2にランキンサイクルの\( \ P-V \ 線図\)の各設備の働きを示します。①給水ポンプで水は高圧になり，②ボイラで蒸気になるため，体積が膨張します。ボイラから出た蒸気は③タービンで断熱膨張して，④復水器で蒸気から水に凝縮します。本問の2つの問題はいずれも実際のタービン，発電機の効率とオーダーが合っているため，知識がある方であれば，計算しなくても解けてしまいます。

【関連する「電気の神髄」記事】

　　火力発電の熱サイクルと熱効率

【解答】

(a)解答：(3)
タービン効率\( \ \eta _{\mathrm {T}} \ \)は，\( \ \displaystyle \eta _{\mathrm {T}}=\frac {タービン出力量W_{\mathrm {OT}}}{タービンが受けた入力量W_{\mathrm {IT}}}\times 100 \ \mathrm {[ ％ ]} \ \)で表される。
ワンポイント解説の通り，タービンが仕事をするのは，\( \ \mathrm {C} \ \)点→\( \ \mathrm {D} \ \)点の間となる。\( \ \mathrm {C} \ \)点の比エンタルピー\( \ \mathrm {3380 \ kJ/kg} \ \)，\( \ \mathrm {D} \ \)点の比エンタルピー\( \ \mathrm {2560 \ kJ/kg} \ \)，蒸気タービンの使用蒸気量\( \ \mathrm {100 \ t/h} \ \)であるから，この蒸気タービンが1時間で受けた入力\( \ W_{\mathrm {IT}} \ \)は，
\[
\begin{eqnarray}
W_{\mathrm {IT}} &=& \left( 3380- 2560 \right) \times 100 \times 10 ^{3} \\[ 5pt ] &=&8.2 \times 10^{7} \ \mathrm { [ kJ/h ] }
\end{eqnarray}
\] となる。一方蒸気タービンの出力\( \ W_{\mathrm {OT}} \ \)は，
\[
\begin{eqnarray}
W_{\mathrm {OT}} &=& 18 \times 10 ^{3}\times 3600 \\[ 5pt ] &=&6.48 \times 10^{7} \ \mathrm { [ kJ/h ] }
\end{eqnarray}
\] となる。よって，タービン効率\( \ \eta _{\mathrm {T}} \ \)は，
\[
\begin{eqnarray}
\eta _{\mathrm {T}} &=& \frac {W_{\mathrm {OT}}}{W_{\mathrm {IT}}} \times 100 \\[ 5pt ] &=& \frac {6.48 \times 10^{7}}{8.2 \times 10^{7}} \times 100 \\[ 5pt ] &≒&79.0 \ \mathrm {[ ％ ]}
\end{eqnarray}
\] と求められる。

(b)解答：(5)
発電機効率\( \ \eta _{\mathrm {G}} \ \)は\( \ \displaystyle \eta _{\mathrm {G}}=\frac {発電機出力P_{\mathrm {G}}}{発電機入力＝タービン出力P_{\mathrm {T}}}\times 100 \ \mathrm {[ ％ ]} \ \)で表される。
題意より，\( \ P_{\mathrm {T}}=18 \ \mathrm {MW} \ \)である。
発電機出力\( \ P_{\mathrm {G}} \ \)は，\( \ \displaystyle 送電端電力=発電機出力P_{\mathrm {G}}\times \frac {100-{所内比率}}{100} \ \)　　であるから，
\[
\begin{eqnarray}
16 &=& P_{\mathrm {G}}\times \frac {100-5}{100} \\[ 5pt ] P_{\mathrm {G}} &≒& 16.84 \ \mathrm {[ MW ]}
\end{eqnarray}
\] となるので，発電機効率\( \ \eta _{\mathrm {G}} \ \)は，
\[
\begin{eqnarray}
\eta _{\mathrm {G}} &=& \frac {P_{\mathrm {G}}}{P_{\mathrm {T}}}\times 100 \\[ 5pt ] &=& \frac {16.84}{18}\times 100 \\[ 5pt ] &≒& 93.6 \ \mathrm {[ ％ ]}
\end{eqnarray}
\] と求められる。