《電力》〈送電〉[H28:問8]架空送電線路の静電誘導障害と電磁誘導障害に関する空欄穴埋問題

Contents

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，誘導障害に関する記述である。

架空送電線と通信線路とが長距離にわたって接近交差していると，通信線路に対して電圧が誘導され，通信設備やその取扱者に危害を及ぼすなどの障害が生じる場合がある。この障害を誘導障害といい，次の\( \ 2 \ \)種類がある。

①　架空送電線路の電圧によって，架空送電線路と通信線路間の\( \ \fbox {　（ア）　} \ \)を介して通信線路に誘導電圧を発生させる\( \ \fbox {　（イ）　} \ \)障害。
②　架空送電線路の電流によって，架空送電線路と通信線路間の\( \ \fbox {　（ウ）　} \ \)を介して通信線路に誘導電圧を発生させる\( \ \fbox {　（エ）　} \ \)障害。

架空送電線路が十分にねん架されていれば，通常は，架空送電線路の電圧や電流によって通信線路に現れる誘導電圧はほぼ\( \ \mathrm {0 \ V} \ \)となるが，架空送電線路で地絡事故が発生すると，電圧及び電流は不平衡になり，通信線路に誘導電圧が生じ，誘導障害が生じる場合がある。例えば，一線地絡事故に伴う\( \ \fbox {　（エ）　} \ \)障害の場合，電源周波数を\( \ f \ \)，地絡電流の大きさを\( \ I \ \)，単位長さ当たりの架空送電線路と通信線路間の\( \ \fbox {　（ウ）　} \ \)を\( \ M \ \)，架空送電線路と通信線路との並行区間長を\( \ L \ \)としたときに，通信線路に生じる誘導電圧の大きさは\( \ \fbox {　（オ）　} \ \)で与えられる。誘導障害対策に当たっては，この誘導電圧の大きさを考慮して検討の要否を考える必要がある。

上記の記述中の空白箇所(ア)，(イ)，(ウ)，(エ)及び(オ)に当てはまる組合せとして，正しいものを次の(1)～(5)のうちから一つ選べ。
\[
\begin{array}{cccccc}
& （ア） & （イ） & （ウ） & （エ） & （オ） \\
\hline
(1) & キャパシタンス & 静電誘導 & 相互インダクタンス & 電磁誘導 & 2\pi fMLI \\
\hline
(2) & キャパシタンス & 静電誘導 & 相互インダクタンス & 電磁誘導 & \pi fMLI \\
\hline
(3) & キャパシタンス & 電磁誘導 & 相互インダクタンス & 静電誘導 & \pi fMLI \\
\hline
(4) & 相互インダクタンス & 電磁誘導 & キャパシタンス & 静電誘導 & 2\pi fMLI \\
\hline
(5) & 相互インダクタンス & 静電誘導 & キャパシタンス & 電磁誘導 & 2\pi fMLI \\
\hline
\end{array}
\]

【ワンポイント解説】

誘導障害は静電誘導障害と電磁誘導障害の二種類があり，名称は似ていますが，メカニズムは全く異なります。よく理解しておきましょう。本問の(ウ)は後半の空白直後の\( \ M \ \)というのが大ヒントとなっています。

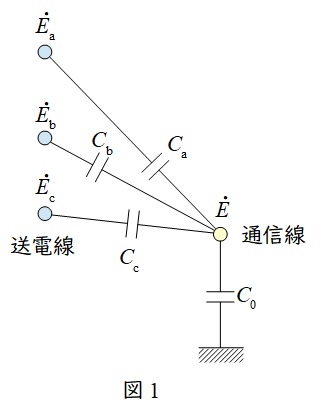
1.静電誘導障害
送電線と通信線間の相互静電容量と通信線と大地間の対地静電容量により，送電線の電圧が分圧されるため発生します。
定量的には，図1の示すように各部電圧と静電容量を定めると，送電線から通信線へ流れる電流の合計は，通信線から大地へ流れる電流と等しいので，
\[
\begin{eqnarray}
\mathrm {j}\omega C_{\mathrm {a}} \left( {\dot E}_{\mathrm {a}}-{\dot E}_{0}\right) +\mathrm {j}\omega C_{\mathrm {b}} \left( {\dot E}_{\mathrm {b}}-{\dot E}_{0}\right) +\mathrm {j}\omega C_{\mathrm {c}} \left( {\dot E}_{\mathrm {c}}-{\dot E}_{0}\right) &=&\mathrm {j}\omega C_{0}{\dot E}_{0} \\[ 5pt ] C_{\mathrm {a}}{\dot E}_{\mathrm {a}}- C_{\mathrm {a}}{\dot E}_{0}+C_{\mathrm {b}}{\dot E}_{\mathrm {b}} -C_{\mathrm {b}}{\dot E}_{0}+C_{\mathrm {c}} {\dot E}_{\mathrm {c}}-C_{\mathrm {c}} {\dot E}_{0} &=& C_{0}{\dot E}_{0} \\[ 5pt ] \left( C_{\mathrm {a}}+C_{\mathrm {b}}+C_{\mathrm {c}}+C_{0}\right) {\dot E}_{0}&=&C_{\mathrm {a}}{\dot E}_{\mathrm {a}}+C_{\mathrm {b}}{\dot E}_{\mathrm {b}}+C_{\mathrm {c}} {\dot E}_{\mathrm {c}} \\[ 5pt ] {\dot E}_{0}&=&\frac {C_{\mathrm {a}} {\dot E}_{\mathrm {a}}+C_{\mathrm {b}} {\dot E}_{\mathrm {b}}+C_{\mathrm {c}} {\dot E}_{\mathrm {c}}}{C_{\mathrm {a}}+C_{\mathrm {b}}+C_{\mathrm {c}}+C_{0}} \\[ 5pt ] \end{eqnarray}
\] となります。ここで，よくねん架された送電線であれば，静電容量は等しくなり，\({\dot E}_{0}≒0\)となります。

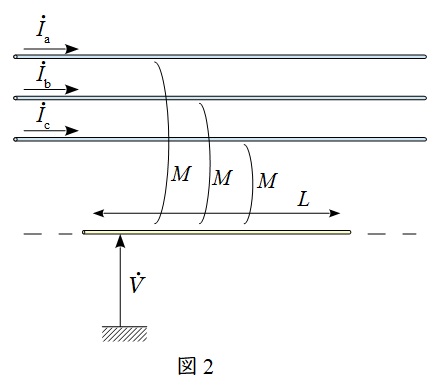
2.電磁誘導障害
送電線と通信線との相互インダクタンスと送電線に流れる各電流の電磁誘導により誘導電圧が発生します。
定量的には，図2のように各電流と相互インダクタンス\( \ M \ \)と並行区間長\( \ L \ \)を定めると，通信線に発生する電圧\( \ {\dot V}_{0} \ \)は，
\[
\begin{eqnarray}
{\dot V}_{0}&=&\mathrm {j}\omega ML {\dot I}_{\mathrm {a}}+\mathrm {j}\omega ML {\dot I}_{\mathrm {b}}+\mathrm {j}\omega ML {\dot I}_{\mathrm {c}} \\[ 5pt ] &=&\mathrm {j}\omega ML \left( {\dot I}_{\mathrm {a}}+{\dot I}_{\mathrm {b}}+{\dot I}_{\mathrm {c}} \right)
\end{eqnarray}
\] となります。通常運転時，\( \ {\dot I}_{\mathrm {a}}+{\dot I}_{\mathrm {b}}+{\dot I}_{\mathrm {c}} ≒0 \ \)であるので，\( \ {\dot V}_{0}≒0 \ \)となります。