《電力》〈配電〉[H29:問17]三相3線式送電線の力率改善に関する計算問題

【問題】

【難易度】★★★★☆（やや難しい）

特別高圧三相3線式専用一回線で，\( \ 6000 \ \mathrm {kW} \ \)(遅れ力率\( \ 90 \ ％ \ \))の負荷\( \ \mathrm {A} \ \)と\( \ 3000 \ \mathrm {kW} \ \)(遅れ力率\( \ 95 \ ％ \ \))の負荷\( \ \mathrm {B} \ \)に受電している需要家がある。
次の(a)及び(b)の問に答えよ。

(a)　需要家全体の合成力率を\( \ 100 \ ％ \ \)にするために必要な力率改善用コンデンサの総容量の値\( \ [\mathrm {kvar}] \ \)として，最も近いものを次の(1)～(5)のうちから一つ選べ。

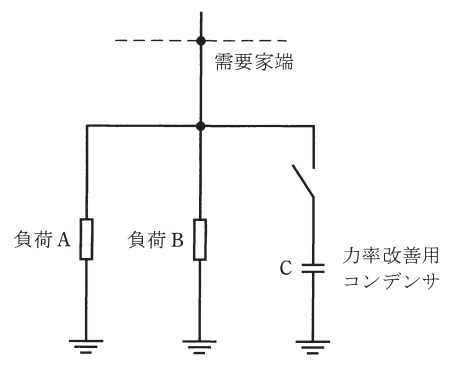
　(1)　\(1430\)　　(2)　\(2900\)　　(3)　\(3550\)　　(4)　\(3900\)　　(5)　\(4360\)

(b)　力率改善用コンデンサの投入・開放による電圧変動を一定値に抑えるために力率改善用コンデンサを分割して設置・運用する。下図のように分割設置する力率改善用コンデンサのうちの\( \ 1 \ \)台(\( \ \mathrm {C1} \ \))は容量が\( \ 1000 \ \mathrm {kvar} \ \)である。\( \ \mathrm {C1} \ \)を投入したとき，投入前後の需要家端Dの電圧変動率が\( \ 0.8 \ ％ \ \)であった。需要家端Dから電源側を見たパーセントインピーダンスの値\( \ [％] \ \)(\( \ 10 \ \mathrm {MV\cdot A} \ \)ベース)として，最も近いものを次の(1)～(5)のうちから一つ選べ。
ただし，線路インピーダンス\( \ X \ \)はリアクタンスのみとする。また，需要家構内の線路インピーダンスは無視する。

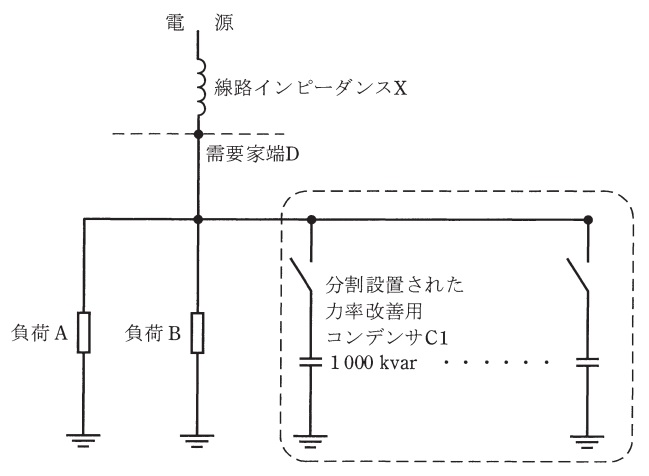
　(1)　\(1.25\)　　(2)　\(8.00\)　　(3)　\(10.0\)　　(4)　\(12.5\)　　(5)　\(15.0\)

【ワンポイント解説】

(a)は難易度は普通ですが，(b)は難易度が高い問題です。電圧降下の式と％インピーダンスの両方を理解していないと解くことができません。得点率\( \ 60 \ ％ \ \)を想定しているならば，(b)はパスしても構わないと思います。

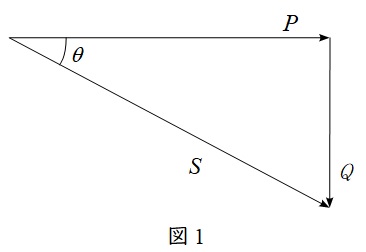
1.有効電力・無効電力と力率の関係
図1において，皮相電力\( \ S=P+\mathrm {j}Q \ \)とし，力率が\( \ \cos\theta \ \)である時，
\[
\begin{eqnarray}
P&=&S\cos\theta \\[ 5pt ] Q&=&S\sin\theta=S\sqrt {1-\cos ^{2}\theta } \\[ 5pt ] \end{eqnarray}
\] より，\( \ S \ \)を消去すると，
\[
\begin{eqnarray}
Q&=&P\cdot \frac {\sqrt {1-\cos ^{2}\theta }}{\cos \theta } \\[ 5pt ] \end{eqnarray}
\] となります。

2.百分率インピーダンスの定義
基準容量\( \ P_{\mathrm {n}} \ \)，基準電圧\( \ V_{\mathrm {n}} \ \)，基準電流\( \ I_{\mathrm {n}} \ \)とすると，インピーダンス\( \ Z \ \mathrm {[\Omega ]} \ \)の百分率インピーダンス\( \ ％Z \ \mathrm {[％]} \ \)は
\[
\begin{eqnarray}
％Z&=&\frac {ZI_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}}\times 100 \\[ 5pt ] &=&\frac {\sqrt {3}ZI_{\mathrm {n}}}{V_{\mathrm {n}}}\times 100 \\[ 5pt ] \end{eqnarray}
\] で定義されます。\( \ P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} \ \)の関係を用いて，定義式を整理すると，
\[
\begin{eqnarray}
％Z&=&\frac {\sqrt {3}ZV_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ] &=&\frac {ZP_{\mathrm {n}}}{V_{\mathrm {n}}^{2}}\times 100 \\[ 5pt ] \end{eqnarray}
\] となります。

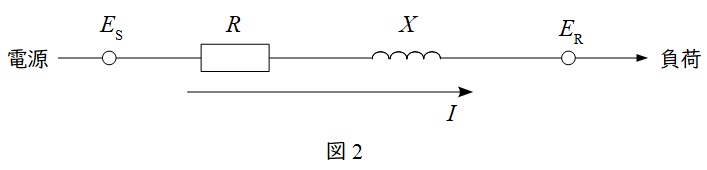
3.送電線・配電線の電圧降下\( \ e \ \)
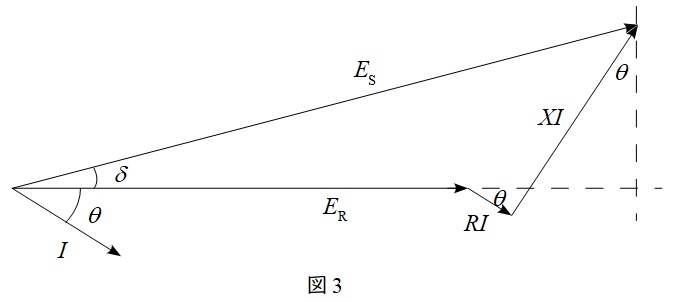
図2の送電線において，送電端の相電圧\( \ E_{\mathrm {S}} \ \)，受電端の相電圧\( \ E_{\mathrm {R}} \ \)，送電線の抵抗\( \ R \ \)，送電線のリアクタンス\( \ X \ \)とすると，一相分のベクトル図は図3のように描けます。この時，\( \ E_{\mathrm {S}} \ \)と\( \ E_{\mathrm {R}} \ \)の相差角\( \ \delta \ \)が十分に小さいとすると，電圧降下\( \ e \ \)は，三相分であることを考慮すると，
\[
\begin{eqnarray}
e&=&E_{\mathrm {S}}-E_{\mathrm {R}}&=&\sqrt {3}I(R\cos\theta +X\sin\theta ) \\[ 5pt ] \end{eqnarray}
\] と近似することができます。

【解答】

(a)解答：(4)
需要家全体の合成力率を\( \ 100 \ ％ \ \)にするためには，全体の無効電力が零になるように力率改善用コンデンサの容量を設定しなければならない。負荷\( \ \mathrm {A} \ \)及び負荷\( \
\mathrm {B} \ \)の無効電力\( \ Q_{\mathrm {A}} \ \)及び\( \ Q_{\mathrm {B}} \ \)は，
\[
\begin{eqnarray}
Q_{\mathrm {A}}&=&P_{\mathrm {A}}\cdot \frac {\sqrt {1-\cos ^{2}\theta _{\mathrm {A}} }}{\cos \theta _{\mathrm {A}} } \\[ 5pt ] &=&6000\times \frac {\sqrt {1-0.9^{2}}}{0.9} \\[ 5pt ] &≒&2905.9 \\[ 5pt ] Q_{\mathrm {B}}&=&P_{\mathrm {B}}\cdot \frac {\sqrt {1-\cos ^{2}\theta _{\mathrm {B}} }}{\cos \theta _{\mathrm {B}} } \\[ 5pt ] &=&3000\times \frac {\sqrt {1-0.95^{2}}}{0.95} \\[ 5pt ] &≒&986.1 \\[ 5pt ] \end{eqnarray}
\] よって，力率改善用コンデンサの容量は，
\[
\begin{eqnarray}
Q_{\mathrm {A}}+Q_{\mathrm {B}}&=&2905.9+986.1 \\[ 5pt ] &=&3892　→　3900 [\mathrm {kvar}] \\[ 5pt ] \end{eqnarray}
\] と求められる。

(b)解答：(2)
ワンポイント解説「3.送電線・配電線の電圧降下\( \ e \ \)」より，題意における電圧降下\( \ e \ \)は，線路インピーダンス\( \ X \ \)はリアクタンス分のみであるから，
\[
\begin{eqnarray}
e&=&\sqrt {3}XI\sin\theta　・・・・・・・　① \\[ 5pt ] \end{eqnarray}
\] となる。ここで，力率改善用コンデンサ\( \ \mathrm {C1} \ \)の無効電力\( \ Q_{\mathrm {C1}} \ \)は，
\[
\begin{eqnarray}
Q_{\mathrm {C1}}&=&\sqrt {3}VI\sin\theta　・・・・・・・　② \\[ 5pt ] \end{eqnarray}
\] であるので，
\[
\begin{eqnarray}
e&=&\sqrt {3}XI\sin\theta \\[ 5pt ] &=&\frac {\sqrt {3}XVI\sin\theta}{V} \\[ 5pt ] &=&\frac {XQ_{C1}}{V} \\[ 5pt ] \end{eqnarray}
\] となる。ここで，\( \ 10 \ \mathrm {MV\cdot A} \ \)ベースにおける百分率インピーダンス法における各値は，
\[
\begin{eqnarray}
％e=0.8，％Q_{C1}=\frac {1000}{10000}\times 100 =10，％V=100 \\[ 5pt ] \end{eqnarray}
\] であるから，各値を代入すると，
\[
\begin{eqnarray}
0.8&=&\frac {％X\times 10}{100} \\[ 5pt ] \end{eqnarray}
\] となり，\( \ ％X \ \)について整理すると，
\[
\begin{eqnarray}
％X&=&8.0 [ ％ ] \\[ 5pt ] \end{eqnarray}
\] と求められる。