Contents
【問題】
【難易度】★★★★☆(やや難しい)
図のように,高圧配電線路と低圧単相\( \ 2 \ \)線式配電線路が平行に施設された設備において,\( \ 1 \ \)次側が高圧配電線路に接続された変圧器の\( \ 2 \ \)次側を低圧単相\( \ 2 \ \)線式配電線路の\( \ \mathrm {S} \ \)点に接続して,\( \ \mathrm {A} \ \)点及び\( \ \mathrm {B} \ \)点の負荷に電力を供給している。\( \ \mathrm {S} \ \)点における線間電圧を\( \ 107 \ \mathrm {V} \ \),電線\( \ 1 \ \)線当たりの抵抗及びリアクタンスをそれぞれ\( \ 0.3 \ \mathrm {\Omega / km} \ \)及び\( \ 0.4 \ \mathrm {\Omega / km} \ \)としたとき,次の(a)及び(b)の問に答えよ。なお,計算においては各点における電圧の位相差が十分に小さいものとして適切な近似を用いること。
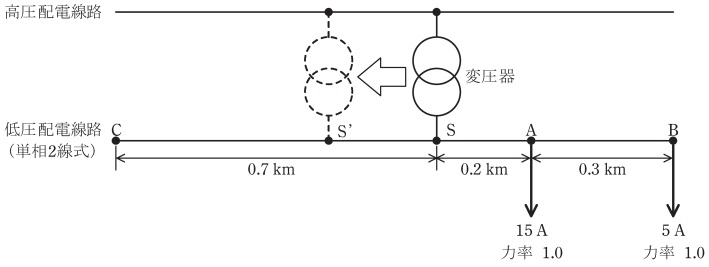
(a) \( \ \mathrm {B} \ \)点における\( \ \mathrm {S} \ \)点に対する電圧降下率の値\( \ \mathrm {[%]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。ただし,電圧降下率は\( \ \mathrm {B} \ \)点受電端電圧基準によるものとする。
(1) \( \ 1.57 \ \) (2) \( \ 3.18 \ \) (3) \( \ 3.30 \ \) (4) \( \ 7.75 \ \) (5) \( \ 16.30 \ \)
(b) \( \ \mathrm {C} \ \)点に電流\( \ 20 \ \mathrm {A} \ \),力率\( \ 0.8 \ \)(遅れ)の負荷が新設されるとき,変圧器を移動して単相\( \ 2 \ \)線式配電線路への接続点を\( \ \mathrm {S} \ \)点から\( \ \mathrm {S}^{\prime } \ \)点に変更することにより,\( \ \mathrm {B} \ \)点及び\( \ \mathrm {C} \ \)点における線間電圧の値が等しくなるようにしたい。このときの\( \ \mathrm {S} \ \)点から\( \ \mathrm {S}^{\prime } \ \)点への移動距離の値\( \ \mathrm {[km]} \ \)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) \( \ 0.213 \ \) (2) \( \ 0.296 \ \) (3) \( \ 0.325 \ \) (4) \( \ 0.334 \ \) (5) \( \ 0.528 \ \)
【ワンポイント解説】
配電線の電圧降下に関する問題です。
単相\( \ 2 \ \)線式であることを認識して電圧降下を\( \ 2 \ \)倍にしないと,誤答を選択し大怪我をする可能性があるので,電圧降下の式はしっかりと区別して理解しておくようにしましょう。
1.配電線の電圧降下の近似式
①単相\( \ 2 \ \)線式送電線の電圧降下
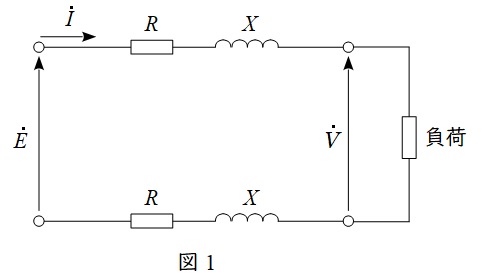
単相\( \ 2 \ \)線式線路は図1のような回路になり,負荷に対して供給される線路と戻りの線路の\( \ 2 \ \)段階で電圧降下が発生します。したがって,負荷の力率が遅れ力率\( \ \cos \theta \ \)であるときのベクトル図を描くと図2のようになります。
図2のベクトル図において,\( \ \dot E \ \)と\( \ \dot V \ \)の位相差が十分に小さいと仮定すると,線路の電圧降下\( \ \varepsilon =E-V \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
E&≃&V+2RI\cos \theta +2XI\sin \theta \\[ 5pt ]
E-V&=&2RI\cos \theta +2XI\sin \theta \\[ 5pt ]
\varepsilon &=&2I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
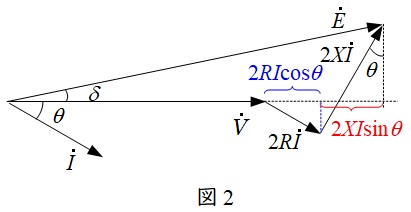
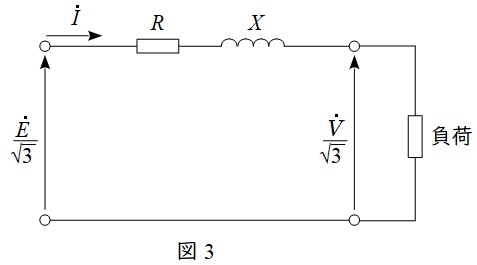
②三相\( \ 3 \ \)線式送電線の電圧降下
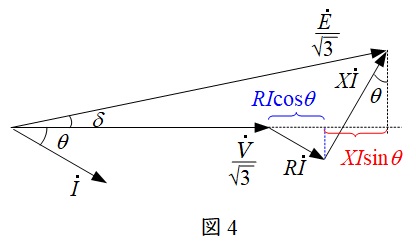
三相回路においては,一相分の等価回路及びベクトル図は図3及び図4のように描くことができ,三相分の電圧降下\( \ \varepsilon \ \mathrm {[V]} \ \)は,
\[
\begin{eqnarray}
\frac {E}{\sqrt {3}}&≃&\frac {V}{\sqrt {3}}+RI\cos \theta +XI\sin \theta \\[ 5pt ]
\frac {E}{\sqrt {3}}-\frac {V}{\sqrt {3}}&=&RI\cos \theta +XI\sin \theta \\[ 5pt ]
E-V&=&\sqrt {3}\left( RI\cos \theta +XI\sin \theta \right) \\[ 5pt ]
\varepsilon &=&\sqrt {3}I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
【解答】
(a)解答:(2)
\( \ \mathrm {A} \ \)点での負荷電流を\( \ I_{\mathrm {A}}=15 \ \mathrm {[A]} \ \),\( \ \mathrm {B} \ \)点での負荷電流を\( \ I_{\mathrm {B}}=5 \ \mathrm {[A]} \ \)とすると,\( \ \mathrm {S} \ \)点と\( \ \mathrm {A} \ \)点の間を流れる電流は,
\[
\begin{eqnarray}
I_{\mathrm {A}}+I_{\mathrm {B}}&=&15+5 \\[ 5pt ]
&=&20 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
である。また,\( \ \mathrm {S} \ \)点から\( \ \mathrm {A} \ \)点までの抵抗\( \ R_{\mathrm {SA}} \ \mathrm {[\Omega ]} \ \)及びリアクタンス\( \ X_{\mathrm {SA}} \ \mathrm {[\Omega ]} \ \),\( \ \mathrm {A} \ \)点から\( \ \mathrm {B} \ \)点までの抵抗\( \ R_{\mathrm {AB}} \ \mathrm {[\Omega ]} \ \)及びリアクタンス\( \ X_{\mathrm {AB}} \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
R_{\mathrm {SA}}&=&0.2\times 0.3 \\[ 5pt ]
&=&0.06 \ \mathrm {[\Omega ]} \\[ 5pt ]
X_{\mathrm {SA}}&=&0.2\times 0.4 \\[ 5pt ]
&=&0.08 \ \mathrm {[\Omega ]} \\[ 5pt ]
R_{\mathrm {AB}}&=&0.3\times 0.3 \\[ 5pt ]
&=&0.09 \ \mathrm {[\Omega ]} \\[ 5pt ]
X_{\mathrm {AB}}&=&0.3\times 0.4 \\[ 5pt ]
&=&0.12 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,ワンポイント解説「1.配電線の電圧降下の近似式」の通り,\( \ \mathrm {S} \ \)点から\( \ \mathrm {B} \ \)点までの電圧降下\( \ \varepsilon \ \mathrm {[V]} \ \)は,力率\( \ \cos \theta =1.0 \left( \sin \theta =0.0 \right) \ \)であることに注意すると,
\[
\begin{eqnarray}
\varepsilon &=&2\left( I_{\mathrm {A}}+I_{\mathrm {B}}\right) \left( R_{\mathrm {SA}} \cos \theta +X_{\mathrm {SA}}\sin \theta \right) +2I_{\mathrm {B}} \left( R_{\mathrm {AB}} \cos \theta +X_{\mathrm {AB}}\sin \theta \right) \\[ 5pt ]
&=&2\left( I_{\mathrm {A}}+I_{\mathrm {B}}\right) R_{\mathrm {SA}} \cos \theta +2I_{\mathrm {B}}R_{\mathrm {AB}} \cos \theta \\[ 5pt ]
&=&2\times \left( 15+5\right) \times 0.06\times 1 +2\times 5 \times 0.09 \times 1 \\[ 5pt ]
&=&2.4 +0.9 \\[ 5pt ]
&=&3.3 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,\( \ \mathrm {B} \ \)点を基準としたときの電圧降下率\( \ %\varepsilon \ \mathrm {[%]} \ \)は,
\[
\begin{eqnarray}
%\varepsilon &=&\frac {\varepsilon }{107-\varepsilon }\times 100 \\[ 5pt ]
&=&\frac {3.3 }{107-3.3 }\times 100 \\[ 5pt ]
&≒&3.18 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(b)解答:(3)
\( \ \mathrm {S} \ \)点から\( \ \mathrm {S}^{\prime } \ \)点への移動距離を\( \ \Delta \mathrm {S} \ \mathrm {[km]} \ \)とする。
\( \ \mathrm {S}^{\prime } \ \)点から\( \ \mathrm {A} \ \)点までの抵抗\( \ R_{\mathrm {SA}}^{\prime } \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
R_{\mathrm {SA}}^{\prime }&=&0.3\left( 0.2+\Delta \mathrm {S}\right) \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
であり,\( \ \mathrm {S}^{\prime } \ \)点から\( \ \mathrm {C} \ \)点までの抵抗\( \ R_{\mathrm {SC}}^{\prime } \ \mathrm {[\Omega ]} \ \)及びリアクタンス\( \ X_{\mathrm {SC}}^{\prime } \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
R_{\mathrm {SC}}^{\prime }&=&0.3\left( 0.7-\Delta \mathrm {S}\right) \ \mathrm {[\Omega ]} \\[ 5pt ]
X_{\mathrm {SC}}^{\prime }&=&0.4\left( 0.7-\Delta \mathrm {S}\right) \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
である。\( \ \mathrm {C} \ \)点の負荷の力率\( \ \cos \theta ^{\prime } =0.8 \ \)であるから,
\[
\begin{eqnarray}
\sin \theta ^{\prime }&=&\sqrt {1-\cos ^{2}\theta ^{\prime }} \\[ 5pt ]
&=&\sqrt {1-0.8^{2}} \\[ 5pt ]
&=&0.6 \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ \mathrm {S}^{\prime } \ \)点からの電圧降下が等しいことから,
\[
\begin{eqnarray}
2\left( I_{\mathrm {A}}+I_{\mathrm {B}}\right) R_{\mathrm {SA}}^{\prime } \cos \theta +2I_{\mathrm {B}}R_{\mathrm {AB}} \cos \theta &=&2I_{\mathrm {C}} \left( R_{\mathrm {SC}}^{\prime } \cos \theta ^{\prime }+X_{\mathrm {SC}}^{\prime }\sin \theta ^{\prime }\right) \\[ 5pt ]
2\times \left( 15+5\right) \times 0.3\left( 0.2+\Delta \mathrm {S} \right) \times 1.0 +2\times 5\times 0.09 \times 1.0 &=&2\times 20 \times \left\{ 0.3\left( 0.7-\Delta \mathrm {S}\right) \times 0.8 +0.4\left( 0.7-\Delta \mathrm {S}\right) \times 0.6 \right\} \\[ 5pt ]
12 \times \left( 0.2+\Delta \mathrm {S} \right) +0.9 &=&40\times \left\{ 0.24\left( 0.7-\Delta \mathrm {S}\right) +0.24\left( 0.7-\Delta \mathrm {S}\right) \right\} \\[ 5pt ]
2.4+12\Delta \mathrm {S} +0.9 &=&40\times \left(0.24+0.24\right) \left( 0.7-\Delta \mathrm {S}\right) \\[ 5pt ]
12\Delta \mathrm {S} +3.3 &=&13.44 -19.2\Delta \mathrm {S} \\[ 5pt ]
31.2\Delta \mathrm {S} &=&10.14 \\[ 5pt ]
\Delta \mathrm {S} &=&0.325 \ \mathrm {[km]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
詳しくは
愛知県出身 愛称たけちゃん
詳しくは